A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án A
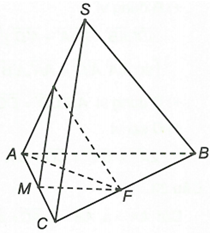
Từ giả thiết suy ra vuông cân tại là tam giác đều.
Có
Vậy
Phương pháp giải
Trong không gian, cho hai vectơ u→ và v→ đều khác 0→ . Tích vô hướng của hai vectơ u→ và v→ là một số, kí hiệu là u→. v→, được xác định bởi công thức:
Trong trường hợp u→ = 0→ hoặc v→ = 0→, ta quy ước u→. v→ = 0
Tham khảo thêm một số tài liệu liên quan:
Chuyên đề vectơ trong không gian, quan hệ vuông góc – bản 1
Chuyên đề vectơ trong không gian, quan hệ vuông góc – bản 2
Chuyên đề vector trong không gian, quan hệ vuông góc – bản 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Chứng minh
Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho . Chứng minh ba vectơ đồng phẳng.
Cho hình hộp ABCD.A'B'C'D'. Gọi G, G' lần lượt là trọng tâm của các tam giác . Chứng minh các điểm thẳng hàng.
Cho hình lăng trụ tam giác ABC.A'B'C' có . Hãy phân tích các vectơ qua các vectơ .
Trong không gian cho ba vectơ . Cho các khẳng định sau.
(1) Nếu các vectơ đồng phẳng thì các vectơ thuộc một mặt phẳng nào đó.
(2) Nếu các vectơ đồng phẳng thì ba vectơ cùng phương.
(3) Nếu tồn tại hai số thực m, n sao cho thì các vectơ đồng phẳng.
(4) Nếu các vectơ đồng phẳng thì giá của chúng song song với mặt phẳng nào đó.
Có bao nhiêu khẳng định đúng?