A.
B.
C.
D.
Giải bởi Vietjack
Chọn đáp án B
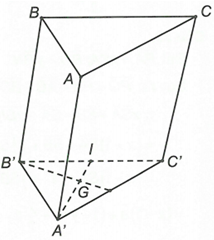
Ta có:
Tích của một số với một vectơ trong không gian
Trong không gian, tích của một số thực k ≠ 0 với một vectơ là một vectơ, kí hiệu là k, được xác định như sau:
- Cùng hướng với vectơ nếu k > 0; ngược hướng với vectơ nếu k < 0.
- Có độ dài bằng .
Trong không gian, phép lấy tích của một số với một vectơ được gọi là phép nhân một số với một vectơ.
Chú ý:
- Quy ước nếu k = 0 hoặc .
- Nếu thì k = 0 hoặc .
- Trong không gian, điều kiện cần và đủ để hai vectơ và (b ≠ 0) cùng phương là có một số thực k sao cho .
Chú ý: Tương tự như phép nhân một số với một vectơ trong mặt phẳng, phép nhân một số với một vectơ trong không gian có các tính chất sau:
- Tính chất kết hợp: Nếu h, k là hai số thực và là một vectơ bất kì thì
- Tính chất phân phối: Nếu h, k là hai số thực và là hai vectơ bất kì thì và .
- Tính chất nhân với 1 và −1: Nếu là một vectơ bất kì thì và .
Chú ý: Tương tự như trong mặt phẳng, nếu G là trọng tâm của tam giác ABC thì với điểm O tùy ý, ta có .
Xem thêm một số kiến thức liên quan:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Chứng minh
Cho tứ diện ABCD. Gọi M và N lần lượt là các điểm trên các cạnh AD và BC sao cho . Chứng minh ba vectơ đồng phẳng.
Cho hình hộp ABCD.A'B'C'D'. Gọi G, G' lần lượt là trọng tâm của các tam giác . Chứng minh các điểm thẳng hàng.
Cho hình lăng trụ tam giác ABC.A'B'C' có . Hãy phân tích các vectơ qua các vectơ .
Trong không gian cho ba vectơ . Cho các khẳng định sau.
(1) Nếu các vectơ đồng phẳng thì các vectơ thuộc một mặt phẳng nào đó.
(2) Nếu các vectơ đồng phẳng thì ba vectơ cùng phương.
(3) Nếu tồn tại hai số thực m, n sao cho thì các vectơ đồng phẳng.
(4) Nếu các vectơ đồng phẳng thì giá của chúng song song với mặt phẳng nào đó.
Có bao nhiêu khẳng định đúng?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
