Cho hình chóp S.ABC, gọi G là trọng tâm của tam giác ABC; M, N lần lượt là trung điềm BC, AC. Giao tuyến của (SAM) và (SBN) là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A

Ta có điểm S, G là hai điểm chung của hai mặt phẳng (SAM) và (SBN) nên
Bài tập liên quan:
Cho hình chóp S.ABC. Gọi M, N lần lượt là hai điểm thuộc vào các cạnh AC và BC, sao cho MN không song song AB. Gọi đường thẳng a là giao tuyến của các mặt phẳng (SMN) và (SAB). Tìm a?
A. , với O là giao điểm của hai đường thẳng AM với BN
B. , với I là giao điểm của hai đường thẳng MN với AB
C. , với Q là giao điểm của hai đường thẳng BM với AN
D. , với I là giao điểm của hai đường thẳng MN với AB
Cách giải:
Đáp án D
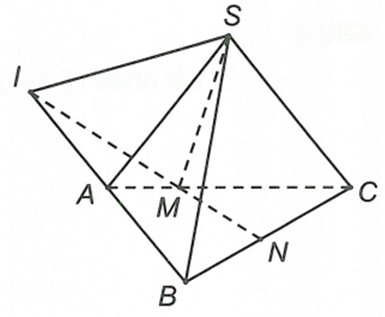
Ta có . Gọi I là giao điểm của MN với AB
Suy ra
Vậy
Tham khảo thêm một số tài liệu liên quan:
Chuyên đề Đại cương về đường thẳng và mặt phẳng 2023 hay, chọn lọc
Phương pháp giải về Hai đường thẳng song song 2023 (lý thuyết và bài tập)
Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O, giao tuyến của mặt (SAC) và (SBD) là
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAD) và (SBD) là đường thẳng
Cho hình chóp S.ABCD có đáy là hình bình hành. M, N lần lượt là trung điểm của BC và SD. Giao tuyến của hai mặt phẳng (AMN) và (SCD) là
Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là
Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của CD và AD, G là trọng tâm tam giác ACD. BG là giao tuyến của hai mặt phẳng nào?
Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của AD và BC. MN là giao tuyến của hai mặt phẳng nào?
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, CD. Tìm giao tuyến của hai mặt phẳng (MBD) và (ABN).
Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC. Gọi K thuộc BD sao cho KD < KB. Gọi E là giao điểm của JK và CD, F là giao điểm của AD và IE. Giao tuyến của (IJK) và (ACD) là
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn). Gọi O là giao điểm của AC và BD, I là giao điểm của AB và CD. Giao tuyến của (SAB) và (SCO) là
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Tìm giao tuyến của mặt phẳng (ACD) và (GAB).
Cho bốn điểm A, B, C, D không đồng phẳng. Trên hai đoạn thẳng AB, AC lần lượt lấy các điểm M, N sao cho và . Tìm giao tuyến của (DMN) và (BCD).