Cho hàm số f(x) liên tục trên R thỏa mãn $\underset{0}{\overset{1}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2$ và $\underset{0}{\overset{2}{\int }}\mathrm{f}(3\mathrm{x}+1)\mathrm{dx}=6$. Tính I = $\underset{0}{\overset{7}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

A = $\underset{0}{\overset{1}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=2$ , B = $\underset{0}{\overset{2}{\int }}\mathrm{f}(3\mathrm{x}+1)\mathrm{dx}=6$

Đặt t = 3x +1 => dt = 3dx

Đổi cận:

Ta có : B = $\frac{1}{3}\underset{1}{\overset{7}{\int }}\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}=6=>\underset{1}{\overset{7}{\int }}\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}=18$

Vậy I = $\underset{0}{\overset{7}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\underset{0}{\overset{1}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\underset{1}{\overset{7}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=20$

Tính chất của tích phân

Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :

 

Một số phương pháp tính tích phân

- Phương pháp đổi biến số

+ Phương pháp đổi biến số dạng 1

Phương pháp chung

• Bước 1: Đặt x = u(t).

• Bước 2: Tính vi phân hai vế: x = u(t) ⇒ dx = u'(t)dt.

Đổi cận: 

• Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t.

Vậy:

+ Phương pháp đổi biến dạng 2

Phương pháp chung

• Bước 1: Đặt u = u(x) ⇒ du = u’(x)dx

• Bước 2: Đổi cận: 

• Bước 3: Chuyển tích phân đã cho sang tích phân theo u.

Vậy:

- Phương pháp tích phân từng phần

Phương pháp chung

• Bước 1: Viết f(x)dx dưới dạng udv = u.v’dx bằng cách chọn một phần thích hợp của f(x) làm u(x) và phần còn lại dv = v'(x)dx

• Bước 2: Tính du = u'dx và v = ∫dv = ∫v'(x)dx

• Bước 3: Tính 

Bài tập liên quan:

Cho hàm số f(x) có đạo hàm liên tục trên tập hợp R$\mathrm{ℝ}$ thỏa mãn 2∫1f(3x−6)dx$\underset{1}{\overset{2}{\int }}\mathrm{f}(3\mathrm{x}-6)\mathrm{dx}$ = 3 và f(−3) = 2. Tính tích phân 0∫−3xf'(x)dx$\underset{-3}{\overset{0}{\int }}\mathrm{xf}\text{'}\left(\mathrm{x}\right)\mathrm{dx}$.

Cách giải:

Đặt t = 3x – 6 => dt = 3dx

Đổi cận :

 

 Do đó: $\underset{1}{\overset{2}{\int }}\mathrm{f}(3\mathrm{x}-6)\mathrm{dx}=\underset{1}{\overset{2}{\int }}\mathrm{f}(3\mathrm{x}-6)\mathrm{dx}=\frac{1}{3}\underset{-3}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}$ = 3

Þ $\underset{-3}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}=9\Rightarrow \underset{-3}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=9$

Đặt $\left\{\begin{array}{c}\mathrm{u}=\mathrm{x}\\ \mathrm{dv}=\mathrm{f}\text{'}\left(\mathrm{x}\right)\mathrm{dx}\end{array}\right.\iff \left\{\begin{array}{c}\mathrm{du}=\mathrm{dx}\\ \mathrm{v}=\mathrm{f}\left(\mathrm{x}\right)\end{array}\right.$

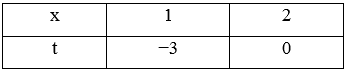
Do đó: $\underset{-3}{\overset{0}{\int }}\mathrm{xf}\text{'}\left(\mathrm{x}\right)\mathrm{dx}={\left.\mathrm{xf}\left(\mathrm{x}\right)\right|}_{-3}^0-\underset{-3}{\overset{0}{\int }}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$ 

= 0.f(0) + 3.f(−3) – 9 = −3.

Tham khảo thêm một số tài liệu liên quan:

Bộ 15 Đề thi Toán 12 Giữa kì 2 năm 2023

30 Đề Thi Thử THPT QG Môn Toán Lớp 12 năm 2021