Với Giải Toán 6 trang 74 Tập 1 Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6. Mời các bạn đón xem:

Giải Toán 6 trang 74 Tập 1 Kết nối tri thức

Luyện tập 2 trang 74 Toán lớp 6 Tập 1: a) Tìm các ước của – 9

b) Tìm các bội của 4 lớn hơn – 20 và nhỏ hơn 20.

Lời giải:

a) Ta có các ước nguyên dương của 9 là: 1; 3; 9

Do đó tất cả các ước của -9 là: -9; -3; -1; 1; 3; 9

b) Lần lượt nhân 4 với 0; 1; 2; 3; 4; 5; 6… ta được các bội dương của 4 là: 0; 4; 8; 12; 16; 20; 24;…

Do đó các bội của 4 là …; -24; -20; -16; -12; -8; -4; 0; 4; 8; 12; 16; 20; 24;…

Vậy các bội của 4 lớn hơn – 20 và nhỏ hơn 20 là -16; -12; -8; -4; 0; 4; 8; 12; 16.

Tranh luận trang 74 Toán lớp 6 Tập 1:

Không biết Tròn tìm được hai số nguyên nào nhỉ?

Lời giải:

Bạn Tròn tìm được hai số nguyên khác nhau mà   và   là hai số đối nhau.

Ví dụ 1: Hai số là 3 và - 3  

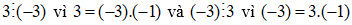
Ví dụ 2: Hai số 12 và - 12           

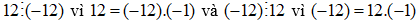
Vậy tổng quát với mọi số nguyên a khác 0. Số đối của a là - a và ta có:

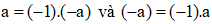
Suy ra a chia hết cho – a và ngược lại (-a) chia hết cho a.

Bài tập

Bài 3.39 trang 74 Toán lớp 6 Tập 1: Tính các thương:

a) 297 : (-3); 

b) (-396) : (-12); 

c) (-600) : 15.

Lời giải:

a) 297 : (-3) = - (297 : 3) = - 99

b) (-396) : (-12) = 396 : 12 = 33

c) (-600) : 15 = - (600 : 15) = - 40.

Bài 3.40 trang 74 Toán lớp 6 Tập 1: a) Tìm các ước của mỗi số: 30; 42; - 50.

b) Tìm các ước chung của 30 và 42.

Lời giải:

a) * Tìm các ước của 30:

Ta có: 30 = 2.3.5

Các ước nguyên dương của 30 là: 1; 2; 3; 5; 6; 10; 15; 30

Do đó tất cả các ước của 30 là:  -30; -15; -10; -6; -5; -3; -2; -1; 1; 2; 3; 5; 6; 10; 15; 30

* Tìm các ước của 42:

Ta có: 42 = 2. 3. 7

Các ước nguyên dương của 42 là: 1; 2; 3; 6; 7; 14; 21; 42

Do đó tất cả các ước của 42 là: -42; -21; -14; -7; -6; -3; -2; -1; 1; 2; 3; 6; 7; 14; 21; 42

* Tìm các ước của – 50:

Ta có 50 = 2.5²

Các ước nguyên dương của 50 là: 1; 2; 5; 10; 25; 50

Do đó tất cả các ước của - 50 là: -50; -25; -10; -5; -2; -1; 1; 2; 5; 10; 25; 50

b) Các ước chung nguyên dương của 30 và 42 là: 1; 2; 3; 6

Do đó các ước chung của 30 và 42 là:  -6; -3; -2; -1; 1; 2; 3; 6. 

Bài 3.41 trang 74 Toán lớp 6 Tập 1: Viết tập hợp sau bằng cách liệt kê phần tử:

 M = {x ∈ Z | x ⁝ 4 và -16 ≤ x < 20 }

Lời giải:

Vì x là số nguyên chia hết cho 4 nên x là bội của 4.

Lần lượt nhân 4 với 0; 1; 2; 3; 4; 5; 6… ta được các bội dương của 4 là: 0; 4; 8; 12; 16; 20; 24;…

Do đó các bội của 4 là: …; -24; -20; -16; -12; -8; -4; 0; 4; 8; 12; 16; 20; 24

Mà các bội của 4 lớn hơn hoặc bằng - 16 và nhỏ hơn 20 là -16; -12; -8; -4; 0; 4; 8; 12; 16

Vậy M = {-16; -12; -8; -4; 0; 4; 8; 12; 16}.

Bài 3.42 trang 74 Toán lớp 6 Tập 1: Tìm hai ước của 15 có tổng bằng – 4.

Lời giải:

Ta có: 15 = 3. 5

Các ước nguyên dương của 15 là: 1; 3; 5; 15

Do đó tất cả các ước của 15 là: -15; -5; -3; -1; 1; 3; 5; 15

Nhận thấy: (- 5) + 1 = - (5 – 1) = - 4;                    (-1) + (- 3) = - (1 + 3) = - 4

Vậy hai ước có tổng bằng 4 là – 5 và 1 hoặc – 1 và – 3.

Bài 3.43 trang 74 Toán lớp 6 Tập 1: Giải thích tại sao: Nếu hai số cùng chia hết cho – 3 thì tổng và hiệu của hai số đó cũng chia hết cho – 3. Hãy thử phát biểu một kết luận tổng quát.

Lời giải:

Giả sử a và b là hai số nguyên cùng chia hết cho -3. Khi đó có hai số nguyên p và q sao cho a = (- 3).p và b = (- 3). q.

+) Ta có: a + b = (-3). p + (- 3). q = (-3). (p + q)

Vì (- 3) $⋮$ (- 3) nên (-3). (p + q) $⋮$(- 3) hay (a + b) $⋮$ (- 3)

 +) Ta có: a - b = (-3). p - (- 3). q = (-3). (p - q) 

Vì (- 3) $⋮$(- 3) nên (-3). (p - q) $⋮$(- 3) hay (a - b) $⋮$(- 3)

Vậy nếu hai số cùng chia hết cho – 3 thì tổng và hiệu của hai số đó cũng chia hết cho – 3.

Tổng quát: Nếu hai số nguyên cùng chia hết cho một số nguyên c (c   0) thì tổng (hay hiệu) của chúng cũng chia hết cho c.

Ta có thể chứng minh kết luận trên như sau:

Giả sử a $⋮$c và b $⋮$ c có nghĩa là a = cp và b = cq (với p, q  ).

Suy ra a + b = cp + cq = c. (p + q).

Vì c $⋮$c nên [c. (p + q)] $⋮$c

Vậy (a + b) $⋮$c.

Xem thêm các bài giải Toán lớp 6 Kết nối tri thức hay, chi tiết khác:

Giải Toán 6 trang 73 Tập 1