Với giải sách bài tập Toán 6 Bài 10: Hai bài toán về phân số sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 10: Hai bài toán về phân số

Bài 105 trang 57 sách bài tập Toán lớp 6 Tập 2: Tính:

a) $\frac{10}{13}$ của 143;

b) $2\frac{1}{2}$ của $7\frac{3}{5}$;

c) $\frac{51}{68}$ của $1\frac{2}{3}$;

d) $\frac{38}{5}$ của $\frac{-5}{19}$;

e) 28% của 50;

g) 0,4 của 125%.

Lời giải:

a) $\frac{10}{13}$ của 143 là $143.\frac{10}{13}=110$;

b) $2\frac{1}{2}$ của $7\frac{3}{5}$ là $7\frac{3}{5}.2\frac{1}{2}=\frac{38}{5}.\frac{5}{2}=\frac{38}{2}=19$;

c) $\frac{51}{68}$ của $1\frac{2}{3}$ là $1\frac{2}{3}.\frac{51}{68}=\frac{5}{3}.\frac{51}{68}=\frac{5}{3}.\frac{17.3}{17.4}=\frac{5}{4}$;

d) $\frac{38}{5}$ của $\frac{-5}{19}$ là $\frac{-5}{19}.\frac{38}{5}=\frac{-5}{19}.\frac{2.19}{5}=-2$;

e) 28% của 50 là $\frac{-5}{19}.\frac{38}{5}=\frac{-5}{19}.\frac{2.19}{5}=-2$;

g) 0,4 của 125% là $125\%.0,4=\frac{125}{100}.\frac{4}{10}=\frac{1}{2}$.

Bài 106 trang 57 sách bài tập Toán lớp 6 Tập 2: Pizza là một loại bánh nổi tiếng của nước Ý và được rất nhiều người yêu thích. Nguyên liệu để làm phần vỏ bánh bao gồm: Bột mì, nước, men, dầu ô liu,… Vỏ bánh muốn đạt yêu cầu thì trong 3 010 g bột bánh cần dùng lượng dầu ô liu bằng $\frac{2}{35}$ số gam bột bánh. Tìm số gam dầu ô liu cần dùng cho 3 010 g bột bánh.

Lời giải:

Số gam dầu ô liu cần dùng cho 3 010 g bột bánh là: $\frac{2}{35}.3010=172$ (gam).

Vậy cần dùng 172 g dầu ô liu cho 3 010 g bột bánh.

Bài 107 trang 57 sách bài tập Toán lớp 6 Tập 2: Tìm một số, biết:

a) $\frac{2}{5}$ của nó bằng 13,5;

b) $3\frac{3}{4}$ của nó bằng $\frac{-13}{27}$;

c) 67% của nó bằng $\frac{134}{7}$;

d) $\frac{4}{5}$ của nó bằng $9\frac{1}{7}$.

Lời giải:

a) $\frac{2}{5}$ của một số bằng 13,5 nên số đó là:

$13,5:\frac{2}{5}=13,5:0,4=33,75$;

b) $3\frac{3}{4}$ của một số bằng $\frac{-13}{27}$ nên số đó là:

$\frac{-13}{27}:3\frac{3}{4}=\frac{-13}{27}:\frac{15}{4}=\frac{-13}{27}.\frac{4}{15}=\frac{-52}{405}$;

c) 67% của một số bằng $\frac{134}{7}$ nên số đó là:

$\frac{134}{7}:\frac{67}{100}=\frac{2.67}{7}.\frac{100}{67}=\frac{200}{7}$;

d) $\frac{4}{5}$ của một số bằng $9\frac{1}{7}$ nên số đó là:

$9\frac{1}{7}:\frac{4}{5}=\frac{64}{7}.\frac{5}{4}=\frac{16.4}{7}.\frac{5}{4}=\frac{80}{7}$.

Bài 108 trang 57 sách bài tập Toán lớp 6 Tập 2: Biết rằng $\frac{9}{10}$ lượng sữa trong hộp là $\frac{3}{4}$ kg. Người ta đã dùng $\frac{3}{5}$ lượng sữa trong hộp. Tìm lượng sữa còn lại trong hộp đó (tính bằng ki-lô-gam).

Lời giải:

Lượng sữa có trong hộp là: $\frac{3}{4}:\frac{9}{10}=\frac{3}{4}.\frac{10}{9}=\frac{5}{6}$ (kg).

Lượng sữa đã dùng là: $\frac{3}{5}.\frac{5}{6}=\frac{1}{2}$ (kg).

Lượng sữa còn lại trong hộp là: $\frac{5}{6}-\frac{1}{2}=\frac{5}{6}-\frac{3}{6}=\frac{2}{6}=\frac{1}{3}$ (kg).

Vậy lượng sữa còn lại trong hộp là $\frac{1}{3}$ kg.

Bài 109 trang 57 sách bài tập Toán lớp 6 Tập 2: Lượng nước trong một loại nấm tươi là $\frac{90}{100}$, trong nấm phơi khô là $\frac{40}{100}$ so với khối lượng của nấm. Nếu một người phơi 30 kg nấm tươi thì thu được bao nhiêu ki-lô-gam nấm khô?

Lời giải:

Lượng nước trong 30 kg nấm tươi là: $30.\frac{90}{100}=27$ (kg).

Khối lượng phần còn lại của nấm có trong 30 kg nấm tươi là:

30 – 27 = 3 (kg).

Lượng nước trong nấm phơi khô là $\frac{40}{100}$ so với khối lượng của nấm nên khối lượng của nấm khô là $1-\frac{40}{100}=\frac{60}{100}=\frac{3}{5}$ so với khối lượng của nấm.

Vậy phơi 30 kg nấm tươi thì thu được lượng nấm khô là: $3:\frac{3}{5}=5$ (kg).

Bài 110 trang 57,58 sách bài tập Toán lớp 6 Tập 2: Ở Thành phố Hồ Chí Minh, công viên Đầm Sen là một trong những công viên văn hóa ở nước ta. Tổng diện tích của công viên là 50 ha, trong đó $\frac{1}{5}$ diện tích là mặt nước, $\frac{3}{5}$ diện tích là cây xanh và vườn hoa, $\frac{3}{100}$ diện tích của phần đất còn lại là Thủy Cung của công viên. Tính diện tích Thủy Cung của công viên Đầm Sen.

Lời giải:

Diện tích mặt nước là: $\frac{1}{5}.50=10$ (ha).

Diện tích cây xanh và vườn hoa là: $\frac{3}{5}.50=30$ (ha).

Diện tích phần đất còn lại là: 50 – (10 + 30) = 10 (ha).

Diện tích Thủy Cung của công viên Đầm Sen là: $\frac{3}{100}.10=0,3$ (ha).

Vậy diện tích Thủy Cung của công viên Đầm Sen là 0,3 ha.

Bài 111 trang 58 sách bài tập Toán lớp 6 Tập 2: Một giỏ đựng một số quả cam. Đầu tiên bác Kiên lấy ra $\frac{1}{2}$ số cam và bớt lại 5 quả, rồi lại lấy $\frac{1}{3}$ số cam còn lại và lấy thêm 4 quả. Cuối cùng số cam còn lại là 12 quả. Lúc đầu trong giỏ có bao nhiêu quả cam?

Lời giải:

Bài toán được mô tả bởi sơ đồ:

+ Số quả cam được biểu diễn bởi đoạn AB;

+ Lấy ra $\frac{1}{2}$ số cam được biểu diễn bởi đoạn AC và sau đó bớt lại 5 quả thì số cam (đoạn CD) đã lấy được biểu diễn bởi đoạn AD, số cam còn lại được biểu diễn bởi đoạn DB;

+ Lấy $\frac{1}{3}$ số cam còn lại được biểu diễn bởi đoạn DE và sau đó lấy thêm 4 quả nữa (đoạn EF) thì số cam còn lại được biểu diễn bởi đoạn FB, tương ứng với 12 quả cam.

Ta có sơ đồ:

Theo sơ đồ, ta thấy $\frac{2}{3}$ số cam còn lại (đoạn EB) sau lần lấy thứ nhất là 4 + 12 = 16 (quả).

Số cam còn lại sau lần lấy thứ nhất (đoạn DB) là: $16:\frac{2}{3}=16.\frac{3}{2}=24$ (quả)

$\frac{1}{2}$ số cam ban đầu (đoạn AC) là: 24 – 5 = 19 (quả)

Vậy số cam trong giỏ ban đầu là: $19:\frac{1}{2}=38$ (quả).

Bài 112 trang 58 sách bài tập Toán lớp 6 Tập 2: Số học sinh trong lớp khoảng 35 đến 50 em. Trong bài kiểm tra môn Tiếng Anh đầu năm, $\frac{1}{7}$ số học sinh đạt loại giỏi, $\frac{1}{3}$ số học sinh đạt loại khá, $\frac{1}{3}$ số học sinh đạt loại trung bình, còn lại đạt loại dưới trung bình. Tìm số học sinh mỗi loại.

Lời giải:

Gọi x (học sinh) là số học sinh của lớp (x ∈ ℕ*).

Khi đó số học sinh đạt loại giỏi là $\frac{1}{7}x$ (học sinh);

Số học sinh đạt loại khá là $\frac{1}{3}x$ (học sinh);

Số học sinh đạt loại trung bình là $\frac{1}{3}x$ (học sinh);

Mà số học sinh mỗi loại là số tự nhiên, do đó $\frac{1}{7}x$; $\frac{1}{3}x$ cũng là số tự nhiên nên x (số học sinh trong lớp)là số tự nhiên chia hết cho cả 3 và 7.

Hay x ∈ BC(3, 7) = {0; 21; 42; …}.

Mà số học sinh trong lớp khoảng 35 đến 50 em nên số học sinh của lớp là 42 học sinh.

Số học sinh đạt loại giỏi là: $\frac{1}{7}.42=6$ (học sinh).

Số học sinh đạt loại khá là: $\frac{1}{3}.42=14$ (học sinh).

Số học sinh đạt loại trung bình là: $\frac{1}{3}.42=14$ (học sinh).

Số học sinh đạt loại dưới trung bình là: 42 – (6 + 14 + 14) = 8 (học sinh).

Vậy số học sinh đạt loại giỏi, khá, trung bình, dưới trung bình lần lượt là 6 học sinh, 14 học sinh, 14 học sinh, 8 học sinh.

Bài 113 trang 58 sách bài tập Toán lớp 6 Tập 2: Tiền lương của một người thợ thủ công trung bình một tháng là 5 000 000 đồng. Mỗi tháng người đó nộp vào quỹ bảo hiểm xã hội $\frac{2}{25}$ số tiền lương, nộp vào bảo hiểm y tế $\frac{3}{200}$ số tiền lương. Mỗi tháng người thợ đó thực lĩnh bao nhiêu tiền?

Lời giải:

Tổng số phần tiền người đó nộp vào quỹ bảo hiểm xã hội và bảo hiểm y tế là:

$\frac{2}{25}+\frac{3}{200}=\frac{19}{200}$ (số tiền lương).

Số tiền thực lĩnh bằng: $1-\frac{19}{200}=\frac{181}{200}$ (số tiền lương).

Số tiền người đó thực lĩnh là: $5000000.\frac{181}{200}=4525000$ (đồng).

Vậy mỗi tháng người thợ đó thực lĩnh là 4 525 000 đồng.

Bài 114 trang 58 sách bài tập Toán lớp 6 Tập 2:

a) Biết rằng $\frac{3}{4}$ lít mật ong nặng $\frac{9}{10}$ kg. 50% của 2 lít mật ong nặng bao nhiêu ki-lô-gam?

b) 72% mảnh vải dài 3,6 m. Cả mảnh vải dài bao nhiêu mét?

Lời giải:

a) 1 lít mật ong nặng: $\frac{9}{10}:\frac{3}{4}=\frac{6}{5}$ (kg).

2 lít mật ong nặng: $2.\frac{6}{5}=\frac{12}{5}$ (kg).

Vậy 50% của 2 lít mật ong nặng: $\frac{12}{5}.\frac{50}{100}=\frac{6}{5}=1\frac{1}{5}$ (kg).

b) Cả mảnh vải dài: $3,6:\frac{72}{100}=5$ (m).

Bài 115 trang 58 sách bài tập Toán lớp 6 Tập 2: Tìm $\frac{13}{4}$ của $1\frac{13}{15}.0,75-\left(\frac{56}{105}+25\%\right).\frac{24}{47}-3\frac{12}{13}:3$.

Lời giải:

Ta có:

$1\frac{13}{15}.0,75-\left(\frac{56}{105}+25\%\right).\frac{24}{47}-3\frac{12}{13}:3$

$=\frac{28}{15}.\frac{75}{100}-\left(\frac{8}{15}+\frac{25}{100}\right).\frac{24}{47}-\frac{51}{13}.\frac{1}{3}$

$=\frac{28}{15}.\frac{3}{4}-\left(\frac{8}{15}+\frac{1}{4}\right).\frac{24}{47}-\frac{17}{13}$

$=\frac{7}{5}-\left(\frac{32}{60}+\frac{15}{60}\right).\frac{24}{47}-\frac{17}{13}$

$=\frac{7}{5}-\frac{47}{60}.\frac{24}{47}-\frac{17}{13}$

$=\frac{7}{5}-\frac{47}{60}.\frac{24}{47}-\frac{17}{13}$

$=\frac{7}{5}-\frac{47}{60}.\frac{24}{47}-\frac{17}{13}$.

Vậy $\frac{13}{4}$ của $\frac{-4}{13}$ là $\frac{13}{4}.\left(\frac{-4}{13}\right)=-1$.

Bài 116 trang 58 sách bài tập Toán lớp 6 Tập 2: Biết rằng lãi suất tiết kiệm là 0,5% một tháng.

a) Để sau một tháng nhận được số tiền lãi là 50 000 đồng thì cần gửi bao nhiêu tiền?

b) Một người gửi tiết kiệm 200 000 000 đồng. Sau một tháng cả tiền lãi và tiền gửi người đó nhận được là bao nhiêu tiền?

Lời giải:

a) Số tiền cần gửi là: 50 000 : 0,5% = 10 000 000 (đồng).

Vậy để sau một tháng nhận được số tiền lãi là 50 000 đồng thì cần gửi 10 000 000 đồng.

b) Số tiền lãi nhận được sau một tháng là:

200 000 000.0,5% = 1 000 000 (đồng).

Số tiền lãi và tiền gửi sau một tháng là:

200 000 000 + 1 000 000 = 201 000 000 (đồng).

Vậy sau một tháng cả tiền lãi và tiền gửi người đó nhận được là 201 000 000 đồng.

Bài 117 trang 58,59 sách bài tập Toán lớp 6 Tập 2: Một người gửi tiết kiệm 6 000 000 đồng. Sau một tháng cả tiền gửi và tiền lãi được 6 030 000 đồng.

a) Tính lãi suất tiết kiệm một tháng.

b) Với mức lãi suất tiết kiệm như thế, nếu người đó gửi 6 000 000 đồng trong hai tháng thì rút ra cả gốc và lãi được tất cả bao nhiêu tiền? Biết rằng tiền gốc và lãi sau tháng thứ nhất được gửi vào tháng thứ hai.

Lời giải:

a) Số tiền lãi sau một tháng gửi là: 6 030 000 – 6 000 000 = 30 000 (đồng).

Lãi suất tiết kiệm một tháng là: $\frac{30000}{6000000}.100\%=0,5\%$.

b) Sau một tháng người đó gửi tiếp 6 030 000 đồng trong một tháng nữa thì số tiền lãi của tháng thứ hai là: 6 030 000.0,5% = 30 150 (đồng)

Vậy sau hai tháng gửi 6 000 000 đồng, nếu người đó rút cả gốc và lãi thì được số tiền là: 6 030 000 + 30 150 = 6 060 150 (đồng).

Bài 118 trang 59 sách bài tập Toán lớp 6 Tập 2: Tính đến tháng 02 năm 2019 dân số của Việt Nam là 97 000 000 người. Nếu tỉ lệ tăng dân số là 1,2% mỗi năm thì đến tháng 02 năm 2021 dân số nước ta dự kiến là bao nhiêu người?

Lời giải:

Đến tháng 02 năm 2020, dân số nước ta dự kiến là:

97 000 000 + 97 000 000.1,2% = 98 164 000 (người).

Vậy đến tháng 02 năm 2021, dân số nước ta dự kiến là:

98 164 000 + 98 164 000.1,2% = 99 341 968 (người).

Bài 119 trang 59 sách bài tập Toán lớp 6 Tập 2: Một quả dưa hấu cân nặng 2 kg chứa 92% nước. Sau khi phơi nắng thì lượng nước trong quả dưa chỉ còn 90% so với khối lượng quả dưa. Khi đó quả dưa cân nặng bao nhiêu ki-lô-gam?

Lời giải:

Lúc đầu, lượng nước chứa trong quả dưa hấu là: 2.92% = 1,84 (kg).

Khối lượng phần còn lại trong quả dưa hấu là: 2 – 1,84 = 0,16 (kg).

Tỉ số phần trăm của phần còn lại đó so với quả dưa hấu đã phơi nắng là:

100% – 90% = 10%.

Vậy khối lượng quả dưa lúc đó là: $0,16:\frac{10}{100}=1,6$ (kg).

Bài 120 trang 59 sách bài tập Toán lớp 6 Tập 2: Trong tháng khuyến mại, một cửa hàng thông báo như sau:

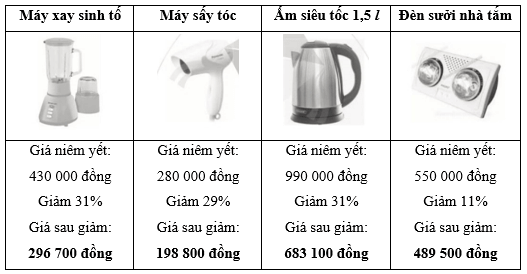
Tính giá tiền sau giảm giá của các mặt hàng trên rồi điền vào chỗ chấm (…).

Lời giải:

⦁ Máy xay sinh tố:

Số tiền được giảm là: 430 000.31% = 133 300 (đồng).

Giá sau giảm của máy xay sinh tố là:

430 000 – 133 300 = 296 700 (đồng).

⦁ Máy sấy tóc:

Số tiền được giảm là: 280 000.29% = 81 200 (đồng)

Giá sau giảm của máy sấy tóc là: 280 000 – 81 200 = 198 800 (đồng).

⦁ Ấm siêu tốc 1,5 l:

Số tiền được giảm là: 990 000.31% = 306 900 (đồng).

Giá sau giảm của ấm siêu tốc 1,5 l là: 990 000 – 306 900 = 683 100 (đồng).

⦁ Đèn sưởi nhà tắm:

Số tiền được giảm là: 550 000.11% = 60 500 (đồng).

Giá sau giảm của đèn sưởi nhà tắm là: 550 000 – 60 500 = 489 500 (đồng).

Vậy ta có bảng sau: