Với giải bài tập Toán lớp 6 Bài 10. Hai bài toán về phân số chi tiết bám sát nội dung sgk Toán 6 Tập 2 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Bài 10. Hai bài toán về phân số - Cánh diều
Trả lời câu hỏi giữa bài
Giải Toán 6 trang 67 Tập 2 Cánh diều
(Nguồn: hftp://en.wikipedia.org)
Tổng chiều dài của 7 chặng leo núi đó khoảng bao nhiêu ki-lô-mét ?
Lời giải:
Tổng chiều dài của 7 chặng leo núi xấp xỉ bằng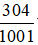 
tổng chiều dài cuộc đua và bằng: .
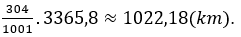
Vậy tổng chiều dài của 7 chặng leo núi đó khoảng: 1022,18km.
Lời giải:
Số ki-lô-mét chị Lan chạy được sau 60 phút là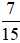 
của 30 km, tức là:
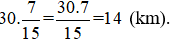
Vậy sau 60 phút chị Lan chạy được 14 km.
Giải Toán 6 trang 68 Tập 2 Cánh diều
Luyện tập 1 trang 68 Toán lớp 6 Tập 2: Tính:
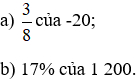
Lời giải:
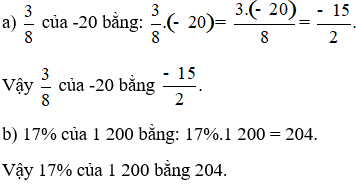
Lời giải:
Do 
số học sinh của lớp 6A là 24 nên số học sinh lớp 6A nhân với bằng 24.
Vậy số học sinh lớp 6A là: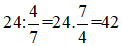 
(học sinh).
Bài tập
Giải Toán 6 trang 69 Tập 2 Cánh diều
Bài 1 trang 69 Toán lớp 6 Tập 2: Tính:
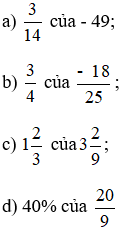
Lời giải:
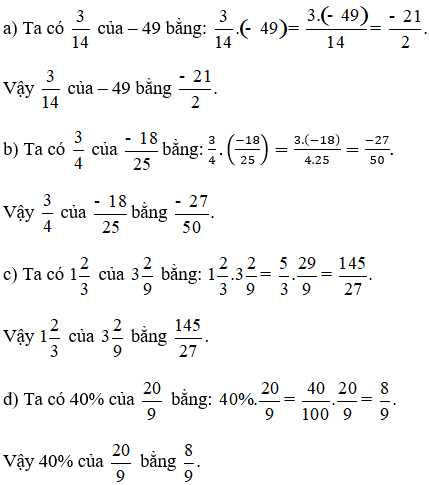
Bài 2 trang 69 Toán lớp 6 Tập 2: Tìm một số, biết:
Lời giải:
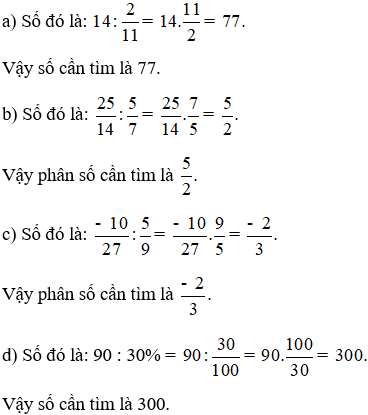
Lời giải:
a) An đem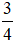 
rác dễ phân huỷ đi đổi cây, biết cứ 3 kg rác dễ phân huỷ đổi được một cây sen đá. Vậy An nhận được bao nhiêu cây sen đá?
b) Số rác khó phân huỷ bạn An thu được bằng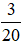 
số rác khó phân huỷ cả đội thu được. Đội của An thu được tất cả bao nhiêu ki-lô-gam rác khó phân huỷ?
Lời giải
a) 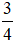rác dễ phân hủy có số ki – lô – gam là: 
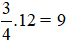(kg).
Vì cứ 3 kg rác dễ phân hủy thì đổi được một cây sen đá nên 9 kg sẽ đổi được 9:3 = 3 (cây).
Vậy bạn An nhận được 3 cây sen đá.
b) Vì số rác khó phân huỷ bạn An thu được bằng 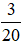số rác khó phân huỷ cả đội thu được nên số rác khó phân hủy của cả đội thu được là: 
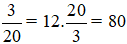(kg).
Vậy số rác khó phân hủy cả đội thu được là: 80 kg.
Giải Toán 6 trang 70 Tập 2 Cánh diều
Lời giải:
Một ngày có 24 giờ
Thời gian ngủ trong một ngày của Gấu túi là: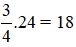 
(giờ).
Thời gian ngủ trong một ngày của con người là: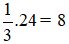 
(giờ).
Một ngày gấu túi ngủ nhiều hơn con người số giờ là: 18 – 8 = 10 (giờ).
Vậy một ngày gấu túi ngủ nhiều hơn con người 10 giờ.
a) Hết kì hạn 1 năm, bác Nhung rút được cả gốc và lãi là bao nhiêu?
b) Giả sử hết kì hạn 1 năm, bác Nhung không rút gốc và lãi thì sau 2 năm, bác Nhung có cả gốc và lãi là bao nhiêu? Biết rằng lãi suất không thay đổi qua hằng năm.
Lời giải:
a) Cách 1: Số tiền lãi sau 1 năm là: 6,8%.10 000 000 = 680 000 (đồng).
Hết kì hạn 1 năm, bác Nhung thu được cả gốc lẫn lãi là:
10 000 000 + 680 000 = 10 680 000 (đồng).
Cách 2: Tính gộp:
Hết kì hạn 1 năm, bác Nhung thu được cả gốc lẫn lãi là:
10 000 000 + 6,8%.10 000 000 = 10 680 000 (đồng).
Vậy sau 1 năm bác Nhung thu được cả gốc lẫn lãi là 10 680 000 đồng.
b) Sau 1 năm nếu không rút tiền thì số tiền bác Nhung có là 10 680 000 đồng. Số tiền này sẽ trở thành tiền gốc của năm thứ hai.
Sau 2 năm, bác Nhung thu được cả gốc lẫn lãi là:
10 680 000 + 6,8%.10 680 000 = 11 406 240 (đồng).
Vậy sau 2 năm bác Nhung thu được cả gốc lẫn lãi là 11 406 240 đồng.
a) Sau 1 năm?
b) Sau 2 năm?
Lời giải:
a) Sau 1 năm, số dân của thành phố A là:
3 + 2%.3 = 3,06 (triệu người).
Vậy sau 1 năm số dân của thành phố A là 3,06 triệu người.
b) Sau 2 năm, số dân của thành phố A là:
3,06 + 2%.3,06 = 3,1212 (triệu người).
Vậy sau 2 năm số dân của thành phố A là 3,1212 triệu người.
Lời giải:
Vì lượng nước trong cỏ tươi là 55% nên cỏ khô (không còn nước) sẽ chiếm 100% - 55% = 45%.
Số ki – lô – gam cỏ tươi cần sấy là: 135 : 45% = 300 (kg).
Vậy để có 135 kg cỏ khô ta cần sấy 300 kg cỏ tươi.
Lời giải:
Số ki – lô – gam cùi dừa cần dùng là: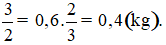 
Số ki – lô – gam đường để cần dùng là: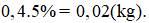 
Vậy đê làm món thịt kho dừa ta cần dùng 0,4 kg cùi dừa và 0,02 kg đường.
Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:
Giải SGK Toán lớp 6 Bài 9: Tỉ số. Tỉ số phần trăm
Giải SGK Toán lớp 6 Bài tập cuối chương 5
Giải SGK Toán lớp 6 Hoạt động thực hành và trải nghiệm. Chủ đề 2. Chỉ số khối cơ thể (BMI)
Giải SGK Toán lớp 6 Bài 1: Điểm. Đường thẳng
Lý thuyết Hai bài toán về phân số
1. Tìm giá trị phân số của một số cho trước
- Muốn tìm giá trị của số a cho trước, ta tính .
Giá trị của m% của số a là giá trị phân số của số a.
- Muốn tìm giá trị m% của số a cho trước, ta tính .
Ví dụ 1. Tính:
a) của 8,7;
b) 25% của 328 mét.
Hướng dẫn giải
a) của 8,7 là: ;
b) 25% của 328 mét là: (m).
2. Tìm một số biết giá trị phân số của số đó
- Muốn tìm một số biết của nó bằng a, ta tính .
- Muốn tìm một số biết m% của nó bằng a, ta tính .
Ví dụ 2. Tìm một số, biết:
a) của nó bằng ‒80;
b) 47% của nó bằng kg.
Hướng dẫn giải
a) của một số bằng ‒80 nên số đó là:
b) 47% của một số bằng kg nên số đó là: (kg).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
thời gian trong ngày để ngủ. Con người dùng 
thời gian trong ngày để ngủ. Trong một ngày gấu túi ngủ nhiều hơn con người là bao nhiêu giờ?
lượng cùi dừa và lượng đường bằng 5% lượng cùi dừa. Nếu có 0,6 kg thịt ba chỉ thì phải cần bao nhiêu ki-lô-gam cùi dừa và bao nhiêu ki-lô-gam đường để làm món thịt kho dừa?