Với giải sách bài tập Toán 6 Bài 5: Số thập phân sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 5: Số thập phân

Bài 53 trang 44 sách bài tập Toán lớp 6 Tập 2: Dưới đây là bảng số liệu của 5 nước châu Âu mà nam giới có chiều cao trung bình cao nhất:

(Nguồn: https://www.yan.vn)

Đọc số liệu trên, cho biết nam giới có chiều cao trung bình cao nhất thuộc nước nào? Thấp nhất thuộc nước nào?

Lời giải:

Đọc bảng số liệu trên ta thấy:

• Chiều cao trung bình của nam giới ở Phần Lan là 181,31 cm.

• Chiều cao trung bình của nam giới ở Na Uy là 182,58 cm.

• Chiều cao trung bình của nam giới ở Thuỵ Điển là 184,61 cm.

• Chiều cao trung bình của nam giới ở Hà Lan là 185 cm.

• Chiều cao trung bình của nam giới ở Đan Mạch là 183,59 cm.

Ta có 185 > 184,61 > 183,59 > 182,58 > 181,31.

Do đó, Hà Lan là nước có chiều cao trung bình của nam giới cao nhất với 185 cm; Phần Lan là nước có chiều cao trung bình của nam giới thấp nhất với 181,31 cm.

Bài 54 trang 44 sách bài tập Toán lớp 6 Tập 2: Hươu cao cổ đực có chiều cao 5,8 m, cá voi xanh dài 33 m, cá mập voi dài 15 m, kì đà Kô-mô-đô dài 3,5 m, trăn mắt võng dài 10,7 m. Hãy đổi các số liệu đo độ dài trên theo đơn vị héc-tô-mét.

Lời giải:

Đổi: 1 m = $\frac{1}{100}$ hm = 0,01 hm.

5,8 m = 0,058 hm.

33 m = 0,33 hm.

15 m = 0,15 hm.

3,5 m = 0,035 hm.

10,7 m = 0,107 hm.

Bài 55 trang 44 sách bài tập Toán lớp 6 Tập 2: Viết các phân số và hỗn số sau đây dưới dạng số thập phân:

$\frac{17}{100};\frac{-100}{1000};\frac{7}{-25};-\frac{19}{4};\frac{26}{65};\frac{45}{-250};2\frac{3}{8};\frac{36}{-400};1\frac{469}{2000}.$

Lời giải:

Ta viết phân số và hỗn số dưới dạng số thập phân như sau:

$\frac{17}{100}=0,17;$

$\frac{-100}{1000}=-0,1;$

$\frac{7}{-25}=\frac{-28}{100}=-0,28;$

$-\frac{19}{4}=-\frac{475}{100}=-4,75;$

$\frac{26}{65}=\frac{2}{5}=\frac{4}{10}=0,4;$

$\frac{45}{-250}=-\frac{9}{50}=-\frac{18}{100}=-0,18;$

$2\frac{3}{8}=2\frac{375}{1000}=2,375;$

$\frac{36}{-400}=-\frac{9}{100}=-0,09;$

$1\frac{469}{2000}=1\frac{2345}{10000}=1,2345.$

Bài 56 trang 44 sách bài tập Toán lớp 6 Tập 2: Viết các số thập phân sau dưới dạng phân số tối giản:

– 0,475; – 0,45; 2,85; 0,31; 0,052; – 2,013; – 0,007.

Lời giải:

Ta viết các số thập phân dưới dạng phân số tối giản như sau:

$–0,475=-\frac{475}{1000}=-\frac{475:25}{1000:25}=-\frac{19}{40};$

$–0,45=-\frac{45}{100}=-\frac{45:5}{100:5}=-\frac{9}{20};$

$2,85=\frac{285}{100}=\frac{285:5}{100:5}=\frac{57}{20};$

$0,31=\frac{31}{100};$

$0,052=\frac{52}{1000}=\frac{52:4}{1000:4}=\frac{13}{250};$

$–2,013=-\frac{2013}{1000};$

$–0,007=-\frac{7}{1000}$.

Bài 57 trang 44 sách bài tập Toán lớp 6 Tập 2: Tìm điều kiện của số tự nhiên n để phân số $\frac{n+2}{300}$ viết được dưới dạng phân số thập phân.

Lời giải:

Ta có $\frac{n+2}{300}=\frac{n+2}{3.100}$ nên $\frac{n+2}{300}$ viết được thành phân số thập phân nếu (n+2) ⋮ 3

Suy ra n + 2 = 3k hay n=3k – 2, k ∈ ℕ*.

Thử lại với n=3k – 2, k ∈ ℕ* ta có:

$\frac{n+2}{300}=\frac{3k-2+2}{300}=\frac{3k}{300}=\frac{k}{100}$

Khi đó $\frac{n+2}{300}$viết được thành phân số thập phân.

Vậy n=3k – 2, k ∈ ℕ*.

Bài 58 trang 44 sách bài tập Toán lớp 6 Tập 2: Sao Thuỷ có bề mặt rất giống với bề mặt của Mặt Trăng và có khối lượng nặng bằng 0,055 lần Trái Đất; Sao Kim có khí quyển nóng bỏng với khối lượng nặng bằng 0,816 lần Trái Đất. Hãy viết các số thập phân trên dưới dạng phân số tối giản.

Lời giải:

Ta viết các số thập phân dưới dạng phân số tối giản như sau:

$0,055=\frac{55}{1000}=\frac{55:5}{1000:5}=\frac{11}{200};$

$0,816=\frac{816}{1000}=\frac{816:8}{1000:8}=\frac{102}{125}$.

Bài 59 trang 44 sách bài tập Toán lớp 6 Tập 2: Viết các số sau theo thứ tự tăng dần:

a) 8,017; 8,107; 8,710; 8,01;

b) 23,049; – 23,051; – 23,105; – 23,150;

c) – 13,5; 3,5; – 2,995; – 7,65;

d) – 0,7; – 0,696; 0,69; 0,609.

Lời giải:

a) 8,017; 8,107; 8,710; 8,01

Ta thấy các số đều có phần nguyên là 8.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 0 < 1 < 7 nên 8,017 < 8,107 < 8,710 và 8,01 < 8,107 < 8,710.

Xét hai số thập phân 8,017 và 8,01 = 8,010.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần nghìn. Do 0 < 7 nên 8,010 < 8,017 hay 8,01 < 8,017.

Vậy viết các số theo thứ tự tăng dần là: 8,01; 8,017; 8,107; 8,710.

b) 23,049; – 23,051; – 23,105; – 23,150

Xét ba số thập phân: 23,051; 23,105;23,150.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 0 < 1 nên 23,051 < 23,105 và 23,051 < 23,150.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau của hai số thập phân 23,105 và 23,150 là cặp chữ số ở vị trí hàng phần trăm. Do 0 < 5 nên 23,105 < 23,150.

Suy ra 23,051 < 23,105 < 23,150.

Nên – 23,051 >– 23,105 > – 23,150.

Mà số thập phân âm luôn nhỏ hơn số thập phân dương nên ta có:

– 23,150 < – 23,105 < – 23,051 < 23,049.

Vậy viết các số theo thứ tự tăng dần là: – 23,150;– 23,105; – 23,051; 23,049.

c) – 13,5; 3,5; – 2,995; – 7,65

Xét ba số thập phân: 13,5;2,995; 7,65.

Do 13 > 7 > 2 nên 13,5 > 7,65 > 2,995.

Do đó – 13,5 < – 7,65 < – 2,995.

Mà số thập phân âm luôn nhỏ hơn số thập phân dương nên ta có:

– 13,5 < – 7,65 < – 2,995 < 3,5.

Vậy viết các số theo thứ tự tăng dần là: – 13,5; – 7,65; – 2,995; 3,5.

d) – 0,7; – 0,696; 0,69; 0,609

Ta chia các số thập phân trên thành hai nhóm:

• Nhóm 1: gồm hai số thập phân âm – 0,7; – 0,696.

• Nhóm 2: gồm hai số thập phân dương 0,69; 0,609.

+ So sánh nhóm 1: – 0,7 và– 0,696.

Xét hai số thập phân 0,7 và 0,696.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 7 > 6 nên 0,7 > 0,696.

Do đó – 0,7 <– 0,696.

+ So sánh nhóm 2: 0,69 và 0,609.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần trăm. Do 0 < 9 nên 0,609 < 0,69.

Mà số thập phân âm luôn nhỏ hơn số thập phân dương nên ta có:

– 0,7 <– 0,696 < 0,609 < 0,69.

Vậy viết các số theo thứ tự tăng dần là: – 0,7;– 0,696; 0,609; 0,69.

Bài 60 trang 45 sách bài tập Toán lớp 6 Tập 2: Bốn bạn Đức, Trung, Kiên, Nguyên cùng đo chiều cao. Đức cao 1,39 m, Trung cao 1 320 mm, Kiên cao một mét rưỡi, Nguyên cao 1 m 390 mm.

a) Bạn nào cao nhất, bạn nào thấp nhất?

b) Những bạn nào có chiều cao bằng nhau?

Lời giải:

Ta có:

Bạn Đức cao 1,39 m = 1 390 mm.

Bạn Trung cao1 320 mm.

Bạn Kiên cao một mét rưỡi tức là 1,5 m = 1 500 mm.

Bạn Nguyên cao1 m 390 mm = 1 390 mm.

Ta có 1 320 mm < 1 390 mm < 1 500 mm.

a) Bạn Kiên cao nhất (1 500 mm), bạn Trung thấp nhất (1 320 mm).

b) Bạn Đức và bạn Nguyêncó chiều cao bằng nhau (cùng bằng 1 390 mm).

Bài 61 trang 45 sách bài tập Toán lớp 6 Tập 2: Chất xơ là một thành phần rất quan trọng trong bữa ăn hằng ngày. Hãy sắp xếp các món ăn trong bảng dưới đây theo thứ tự lượng chất xơ tăng dần.

Lời giải:

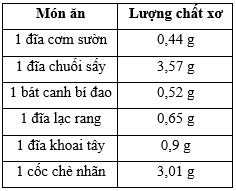
Ta có 0,44 g < 0,52 g < 0,65 g < 0,9 g < 3,01 g < 3,57 g.

Do đó sắp xếp các món ăn theo thứ tự lượng chất xơ tăng dần là: 1 đĩa cơm sườn, 1 bát canh bí đao, 1 đĩa lạc rang, 1 đĩa khoai tây, 1 cốc chè nhãn, 1 đĩa chuối sấy.

Bài 62 trang 45 sách bài tập Toán lớp 6 Tập 2:

1) Tìm số tự nhiên x lớn nhất, biết:

a) x < 3,005; b) x < $\frac{157}{100}$.

2) Tìm số tự nhiên y bé nhất, biết:

a) y > 9,999; b) y > $\frac{2021}{1000}$.

Lời giải:

1) Tìm số tự nhiên x lớn nhất

a) Ta có x < 3,005

Vì x là số tự nhiên nên suy ra x ≤ 3.

Do đó x ∈ {0; 1; 2; 3}.

Mà x là số tự nhiên lớn nhất nên x = 3.

Vậy số tự nhiên lớn nhất cần tìm là x = 3.

b) Ta có x < $\frac{157}{100}$ = 1,57.

Vì x là số tự nhiên nên suy ra x ≤ 1.

Do đó x ∈ {0; 1}.

Mà x là số tự nhiên lớn nhất nên x = 1.

Vậy số tự nhiên lớn nhất cần tìm là x = 1.

2) Tìm số tự nhiên y bé nhất:

a) Ta có y > 9,999

Vì y là số tự nhiên nên suy ra y ≥ 10.

Do đó y ∈ {10; 11; …}.

Mà y là số tự nhiên bé nhất nên y = 10.

Vậy số tự nhiên bé nhất cần tìm là y = 10.

b) Ta có y > $\frac{2021}{1000}$> = 2,021.

Vì y là số tự nhiên nên suy ra y ≥ 3.

Do đó y ∈ {3; 4; …}.

Mà y là số tự nhiên bé nhất nên y = 3.

Vậy số tự nhiên bé nhất cần tìm là y = 3.

Bài 63 trang 45 sách bài tập Toán lớp 6 Tập 2: Tìm hai số tự nhiên liên tiếp m vàn, biết:

a) m < 16,2756<n;

b) n <9,2995<m.

Lời giải:

a) m < 16,2756<n

Do m và n là các số tự nhiên nên ta có m ≤ 16 và n ≥ 17.

Mà m và n là hai số tự nhiên liên tiếp nên m = 16 và n = 17.

Vậy m = 16 và n = 17.

b) n <9,2995<m.

Do m và n là các số tự nhiên nên ta có n ≤ 9 và m ≥ 10.

Mà m và n là hai số tự nhiên liên tiếp nên n = 9 và m = 10.

Vậy m = 10 và n = 9.

Bài 64 trang 45 sách bài tập Toán lớp 6 Tập 2: Cho x

Lời giải:

Ta có b< 1,25 và b là số tự nhiên nên b ∈ {0; 1}.

Với b = 0 thì x < 0, khi đó x không thỏa mãn là số tự nhiên. Ta loại trường hợp này.

Với b = 1 thì x < 1, khi đó số tự nhiên x thỏa mãn là x = 0.

Vậy x = 0.

Bài 65 trang 45 sách bài tập Toán lớp 6 Tập 2:

a) Tìm các số thập phân x có một chữ số ở phần thập phân sao cho: 8<x<9.

b) Tìm các số thập phân x có hai chữ số ở phần thập phân sao cho: 0,1<x<0,2.

Lời giải:

a) Các số thập phân x có một chữ số ở phần thập phân sao cho 8<x<9 là:

x ∈ {8,1; 8,2; 8,3; 8,4; 8,5; 8,6; 8,7; 8,8; 8,9}.

b) Các số thập phân x có hai chữ số ở phần thập phân sao cho 0,1<x<0,2 là:

x ∈ {0,11; 0,12; 0,13; 0,14; 0,15; 0,16; 0,17; 0,18; 0,19}.

Lý thuyết Số thập phân

1. Số thập phân

- Phân số thập phân là phân số mà mẫu là lũy thừa của 10 và tử là số nguyên.

- Phân số thập phân có thể viết được dưới dạng số thập phân.

- Số thập phân gồm hai phần:

+ Phần số nguyên được viết bên trái dấu phẩy;

+ Phần thập phân được viết bên phải dấu phẩy.

Ví dụ 1. Viết các phân số và hỗn số sau dưới dạng số thập phân: $\frac{-27}{100};$ $\frac{1}{25};$   $1\frac{3}{125}$.

Hướng dẫn giải

$\frac{-27}{100}=-0,27;$

$\frac{1}{25}=\frac{1.4}{25.4}=\frac{4}{100}=0,04;$

$1\frac{3}{125}=1+\frac{3}{125}=1+\frac{3.8}{125.8}=1+\frac{24}{1000}=1+0,024=1,024.$

2. So sánh các số thập phân

a) So sánh hai số thập phân

Trong 2 số thập phân khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a < b hay b > a.

- Số thập phân lớn hơn 0 gọi là số thập phân dương.

- Số thập phân nhỏ hơn 0 gọi là số thập phân âm.

- Nếu a < b và b < c thì a < c.

b) Cách so sánh hai số thập phân

* So sánh hai số thập phân khác dấu:

Số thập phân âm luôn nhỏ hơn số thập phân dương.

* So sánh hai số thập phân dương:

Bước 1: So sánh phần số nguyên của hai số thập phân dương đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn.

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng (sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn.

* So sánh hai số thập phân âm:

Nếu a < b thì ‒ a > ‒ b.

Ví dụ 2. Sắp xếp các số thập phân 3,124; –3,105; –3,142; 3,015 theo thứ tự giảm dần.

Hướng dẫn giải

Ta chia các số 3,124; –3,105; –3,142; 3,015 thành hai nhóm:

Nhóm 1 gồm các số 3,124; 3,015.

Nhóm 2 gồm các số –3,105; –3,142.

Ta đi so sánh nhóm 1: 3,124; 3,015.

Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 1 > 0 nên 3,124 > 3,015.

Ta đi so sánh nhóm 2: –3,105; –3,142.

Xét hai số 3,105 và 3,142;

Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần trăm. Mà 0 < 4 nên 3,105 < 3,142. Do đó –3,105 > –3,142.

Nhóm 1 gồm các số thập phân dương, nhóm 2 gồm các số thập phân âm, mà số thập phân dương luôn lớn hơn số thập phân âm.

Do đó 3,124 > 3,015 > –3,105 > –3,142.

Vậy sắp xếp các số theo thứ tự giảm dần là:  3,124; 3,015; –3,105; –3,142.