Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 12 sách Cánh diều năm 2025 - 2026. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 12. Mời các bạn cùng đón xem:
Đề thi giữa kì 1 Toán 12 Cánh diều có đáp án năm 2025
Đề thi giữa kì 1 Toán 12 Cánh diều có đáp án - Đề 1
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
Năm học ..............
Môn: Toán lớp 12
Thời gian làm bài: phút
(Đề số 1)
Câu 1 : Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây sai?
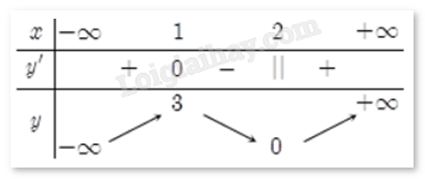
Hàm số đã cho đồng biến trên khoảng
Hàm số đã cho đồng biến trên khoảng
Hàm số đã cho đồng biến trên khoảng
Hàm số đã cho nghịch biến trên khoảng (0;3)
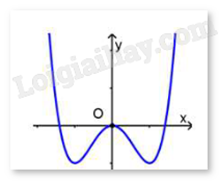
Câu 2 : Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
Câu 3 : Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
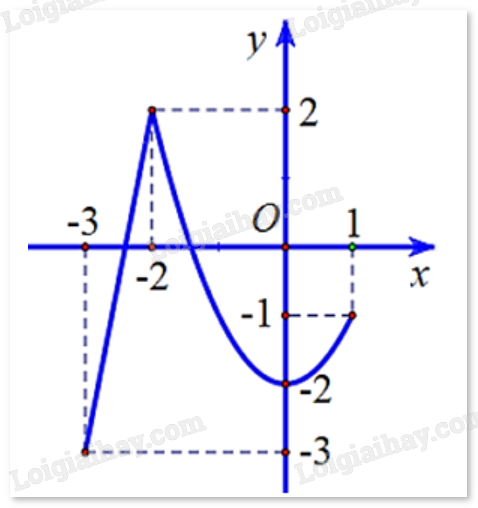
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-3;1]. Tính M + m.
-1
-2
0
-3
Câu 4 : Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
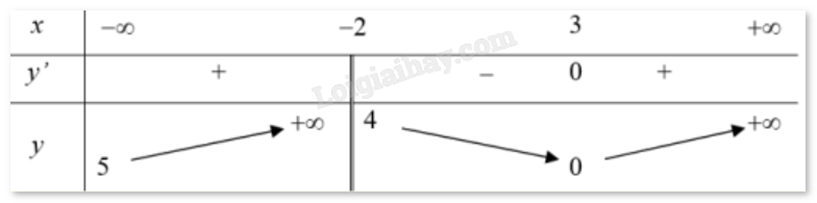
2
3
4
1
Câu 5 : Đường tiệm cận xiên của đồ thị hàm số là:
Câu 6 : Tọa độ tâm đối xứng của đồ thị hàm số là:
(-1;6)
(-1;12)
(1;4)
(-3;28)
Câu 7 : Cho ba vecto không đồng phẳng. Xét các vecto , , . Chọn khẳng định đúng.
Ba vecto đồng phẳng
Hai vecto cùng phương
Hai vecto cùng phương
Ba vecto đôi một cùng phương
Câu 8 : Cho hàm số có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
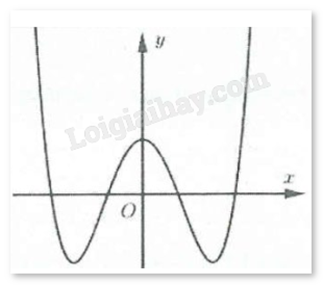
a > 0, b > 0, c < 0
a > 0, b < 0, c > 0
a < 0, b > 0, c > 0
a > 0, b > 0, c > 0
Câu 9 : Giá trị lớn nhất của hàm số là:
8
9
1
3
Câu 11 : Cho tứ diện ABCD có AB = AC = AD và . Hãy xác định góc giữa cặp vecto và .
Câu 12 : Cho hai vecto thỏa mãn và . Độ dài vecto là?
8
124
Cho hàm số f(x) xác định trên R có đồ thị như sau:
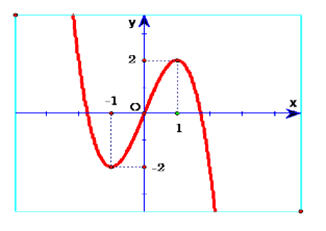
a) Hàm số f(x) đồng biến trên (-1;1)
b) Số điểm cực trị của hàm số đã cho là 2
c) Hàm số f(x) không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là
Cho đồ thị của hàm số f(x) như sau:
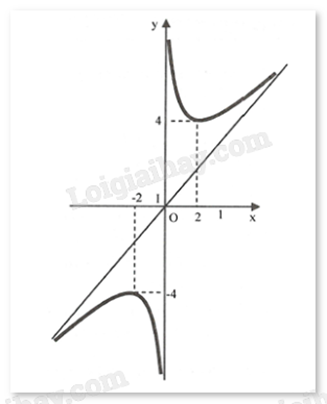
a) Đồ thị hàm số f(x) có tiệm cận đứng và tiệm cận xiên
b) Đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
c) Hàm số f(x) có giá trị lớn nhất là -4
d) Đồ thị hàm số f(x) có điểm cực đại (2;4) và điểm cực tiểu (-2;-4)
Cho hình chóp S.ABCD.
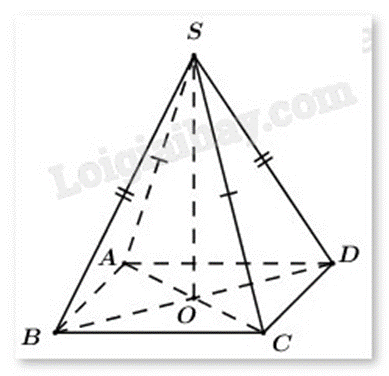
a) Tứ giác ABCD là hình bình hành nếu
b) Tứ giác ABCD là hình bình hành nếu
c) Nếu có thì tứ giác ABCD là hình bình hành
d) Tứ giác ABCD là hình bình hành nếu
Trong không gian Oxyz, cho vecto , .
a)
b)
c)
d) Góc giữa hai vecto bằng
Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số lần lượt là M, m. Tính M + m.
Đáp án:
Tính tổng tất cả các giá trị thực của tham số m để đồ thị hàm số có đúng 2 đường tiệm cận.
Đáp án:
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D’(6;8;10). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng bao nhiêu?
Đáp án:
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức , trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng milligram). Tính liều lượng thuốc cần tiêm (đơn vị milligram) cho bệnh nhân để huyết áp giảm nhiều nhất.
Đáp án:
Giá trị của tham số m để đồ thị hàm số có hai điểm cực trị A, B thỏa mãn OA = OB (O là gốc tọa độ) có dạng là một phân số tối giản. Tính a + b.
Đáp án:
Cho hàm số y = f(x) có đồ thị như hình:
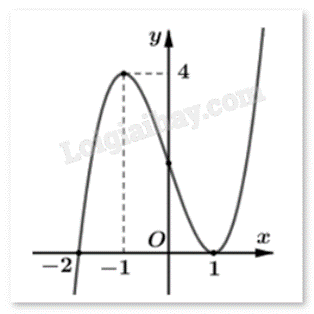
Tìm số điểm cực trị của hàm số .
Đáp án:
ĐÁP ÁN
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
| 1. D | 2. D | 3. A | 4. A | 5. D | 6. B |
| 7. A | 8. B | 9. B | 10. A | 11. D | 12. B |
a) Đúng. Hàm số f(x) đồng biến trên (-1;1).
b) Đúng. Hàm số có 2 điểm cực trị là x = 1; x = -1.
c) Đúng. Hàm số đã cho không có giá trị lớn nhất và nhỏ nhất.
d) Sai. Đồ thị hàm số là .
a) Đúng. Đồ thị hàm số f(x) có tiệm cận đứng x = 0 và tiệm cận xiên y = 2x.
b) Đúng. Vì gốc tọa độ O là trung điểm của 2 cực trị (2;4) và (-2;-4) nên là tâm đối xứng của đồ thị.
c) Sai. Hàm số không có giá trị lớn nhất.
d) Sai. Đồ thị hàm số f(x) có điểm cực tiểu (2;4) và điểm cực đại (-2;-4) .
a) Sai. chưa phải là điều kiện đủ để tứ giác ABCD là hình bình hành.
b) Sai. Tứ giác ABCD là hình bình hành nếu .
c) Đúng. Vì
suy ra ABCD là hình bình hành (theo quy tắc hình bình hành).
d) Sai. Vì tứ giác ABCD là hình bình hành nếu .
a) Đúng. Vì .
b) Đúng. Vì .
c) Sai. Vì .
d) Sai. Vì
nên góc giữa hai vecto bằng xấp xỉ .
Tập xác định: D = [-1;1].
Ta có:
f(-1) = f(1) = 0; ; .
Vậy .
Ta luôn có một đường tiệm cận ngang y = 1.
Đồ thị hàm số có đúng 2 đường tiệm cận khi và chỉ khi có nghiệm x = 1 hoặc x = 2.
Khi x = 1 thì m = -1. Khi x = 2 thì m = -4. Vậy tổng các giá trị của m là -1 + (-4) = -5.
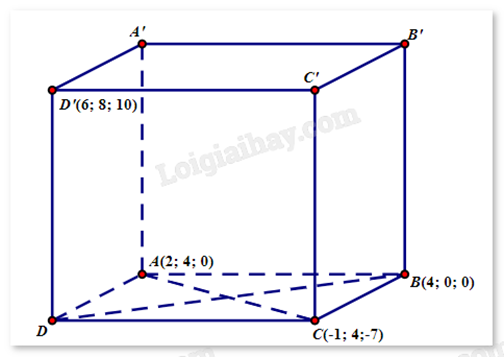
Giả sử D(a;b;c), B’(a’;b’;c’). Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC.
Từ đó, ta tính được tọa độ điểm O.
Vì O là trung điểm của BD nên từ B(4;0;0) ta tìm được D(-3;8;-7).
Vậy, . Mà ABCD.A’B’C’D’ là hình hộp nên .
Mà , suy ra a’ = 13, b’ = 0, c’ = 17.
Vậy B’(13;0;17). Tổng hoành độ, tung độ, cao độ của điểm B’ bằng 13 + 0 + 17 = 30.
Xét G(x) trên đoạn [0;15].
Ta có: .
Mặt khác, G(15) = 0; G(10) = 17,5; G(15) = 0. Vậy x cần tìm là 10.
Tập xác định: D = R.
Do đó, đồ thị hàm số đã cho luôn có 2 điểm cực trị lần lượt có tọa độ là A(0; m) và B(2; -4 + m).
Ta có:
.
Vậy a = 5, b = 2. Suy ra a + b = 5 + 2 = 7.
Ta có: .
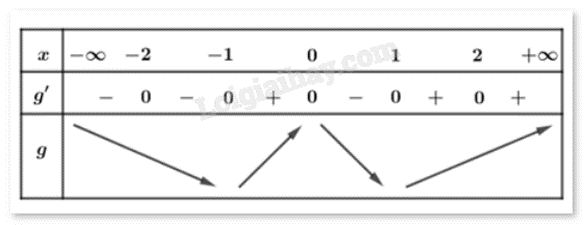
Vì f’(x) không đổi dấu khi qua x = 1 nên g(x) có 3 điểm cực trị.
Đề thi giữa kì 1 Toán 12 Cánh diều có đáp án - Đề 2
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
Năm học ..............
Môn: Toán lớp 12
Thời gian làm bài: phút
(Đề số 2)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như sau:
Phát biểu nào dưới đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng (-1;1).
B. Hàm số đã cho đồng biến trên mỗi khoảng (-∞;-2) và (2;+∞).
C. Hàm số đã cho nghịch biến trên khoảng (0;1).
D. Hàm số đã cho nghịch biến trên khoảng (-1;1).
Câu 2. Cho hàm số y = f(x) xác định và liên tục trên [-2;3] và có bảng xét dấu như sau:
Hàm số đã cho đạt cực đại tại điểm
A. x = -2.
B. x = 0.
C. x = 1.
D. x = 3.
Câu 3. Cho hàm số y = f(x) liên tục và có bảng biến thiên trên đoạn [-1;3] như hình dưới đây.
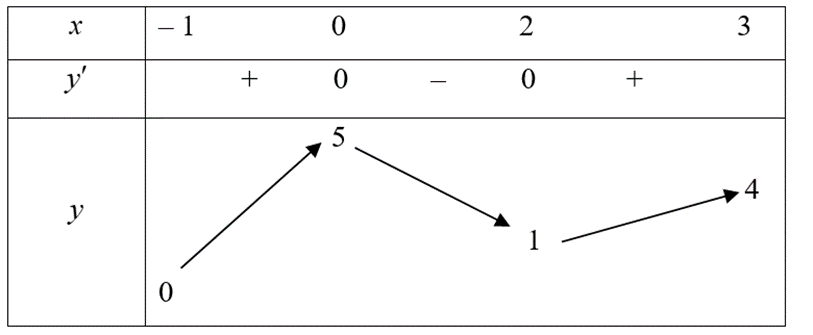
Gọi M là giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;3]. Mệnh đề nào trong các mệnh đề sau đây là đúng?
A. M = f(-1).
B. M = f(3).
C. M = f(2).
D. M = f(0).
Câu 4. Cho hàm số y = f(x) có bảng biến thiên như sau:
Đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số đã cho lần lượt là:
A. x = 2, y = -1.
B. x = -1, y =2.
C. x = -1, y = -1.
D. x = 2, y = 1.
Câu 5. Tiệm cận xiên của đồ thị hàm số là đường thẳng
A. y = 2x.
B. y = 2x - 1.
C. y = 2x + 1.
D. y = x + 1.
Câu 6. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
Tâm đối xứng của đồ thị hàm số có tọa độ là
A. (1;0).
B. (-1;1).
C. (-1;-2).
D. (-1;0).
Câu 7. Cho hình hộp ABCD.A'B'C'D'.
Khẳng định nào sau đây là sai?
A. .
B. .
C. .
D. .
Câu 8. Hàm số nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-2;4).
B. (-2;1).
C. (-2;+∞).
D. (4;+∞).
Câu 9. Giá trị lớn nhất của hàm số y = x3 -3x + 6 trên đoạn [0;2] bằng
A. 0.
B. 3.
C. 5.
D. 7.
Câu 10. Đường cong trong hình dưới là đồ thị của hàm số nào trong bốn hàm số sau đây?
A. y = x3 - 4x + 1.
B. y = x3 + 3x2 + 1.
C. y = x3 - 4x - 1.
D. y = -x3 + 4x + 1.
Câu 11. Cho hàm số có đồ thị như hình vẽ dưới đây.
Khẳng định nào sau đây là đúng?
A. a > 0, b > 0. c > 0, d < 0.
B. a > 0, b < 0. c > 0, d < 0.
C. a > 0, b < 0. c < 0, d < 0.
D. a > 0, b > 0. c < 0, d > 0.
Câu 12. Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của các cạnh AB và CD. Đặt . Khẳng định nào sau đây là đúng?
A. .
B. .
C. .
D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số (với a ≠ 0) có đồ thị là đường cong như hình dưới đây.
a) Hàm số đã cho nghịch biến trên ℝ\{2}.
b) Hàm số đã cho đạt cực đại tại x = -3; đạt cực tiểu tại x = -1.
c) Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng y = -2.
d) Công thức xác định hàm số đã cho là .
Câu 2. Cho hàm số y = f(x) = x3 - 3x2 - 9x + 5.
a) Hàm số đã cho đồng biến trên mỗi khoảng (-∞;-1) và (3;+∞).
b) Giá trị cực đại của hàm số đã cho là -1.
c) Đồ thị hàm số đã cho đi qua các điểm (0;5), (1;-6), (-1;-10).
d) Đường thẳng y = -22 cắt đồ thị hàm số đã cho tại 3 điểm phân biệt.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. G là điểm thỏa mãn . Khi đó:
a) .
b) .
c) .
d) .
Câu 4. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó:
a) .
b) .
c) .
d) Với M, N lần lượt là trung điểm của AD,BB' thì .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho a ≠ 0, b2 - 3ac > 0. Hàm số y = ax3 + bx2 + cx + d có tất cả bao nhiêu điểm cực trị?
Câu 2. Cho hàm số với m là tham số thực. Gọi m1, m2 là hai giá trị của m thỏa mãn . Giá trị của biểu thức m1 + m2 bằng bao nhiêu?
Câu 3. Cho hình hộp ABCD.A'B'C'D'. Tìm giá trị thực của k thỏa mãn đẳng thức .
Câu 4. Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B, hay có thể chèo trực tiếp đến B, hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B. Biết anh ấy có thể chèo thuyền 6 km/h, chạy 8 km/h và quãng đường BC = 8 km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Khoảng thời gian ngắn nhất để người đàn ông đến B là bao nhiêu giờ (làm tròn kết quả đến hàng phần mười)?
Câu 5. Cho một tấm nhôm hình vuông cạnh 12 cm, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).
Giá trị của x bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
Câu 6. Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho các lực căng lần lượt trên mối dây OA, OB, OC đôi một vuông góc với nhau và (N) (như hình vẽ). Trọng lượng của chiếc đèn tròn đó là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị)?
----------HẾT----------