Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 12 sách Kết nối tri thức năm 2025 - 2026. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 12. Mời các bạn cùng đón xem:
Đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án năm 2025
Đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 1
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Kết nối tri thức
Năm học ...............
Môn: Toán lớp 12
Thời gian làm bài: phút
(Đề số 1)
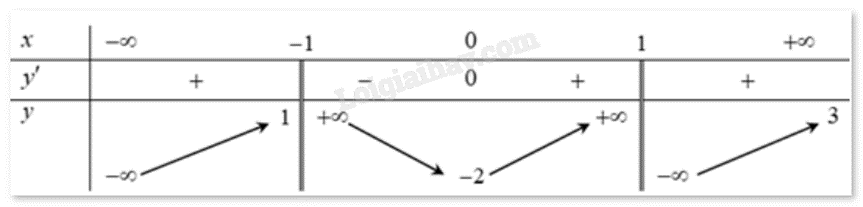
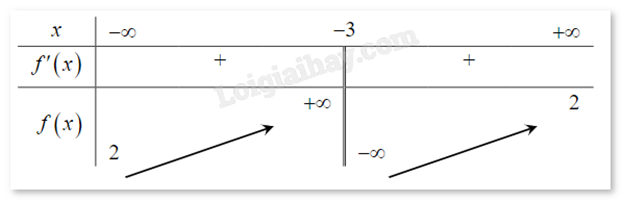
Câu 1 : Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng
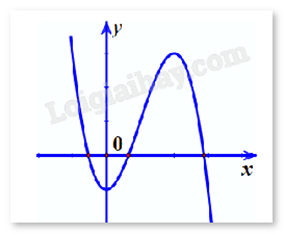
Câu 2 : Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
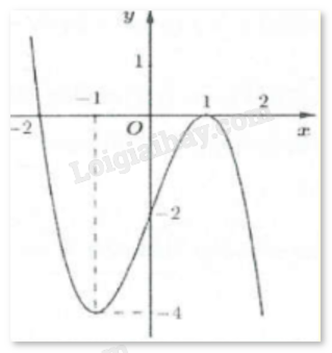
Câu 3 : Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Tính M - m.
1
2
3
4
Câu 4 : Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
1
4
2
3
Câu 5 : Đường tiệm cận xiên của đồ thị hàm số là:
Câu 6 : Tọa độ tâm đối xứng của đồ thị hàm số là:
(3;-2)
(-2;3)
(2;-3)
(-3;2)
Câu 7 : Trong các mệnh đề sau, mệnh đề nào sai?
Vì I là trung điểm đoạn AB nên từ O bất kì ta có:
Vì nên bốn điểm A, B, C, D đồng phẳng
Vì nên N là trung điểm của đoạn NP
Từ hệ thức ta suy ra ba vecto đồng phẳng
Câu 8 : Cho hàm số có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?
Câu 9 : Đường cong hình bên là đồ thị của hàm số . Khẳng định nào sau đây đúng?
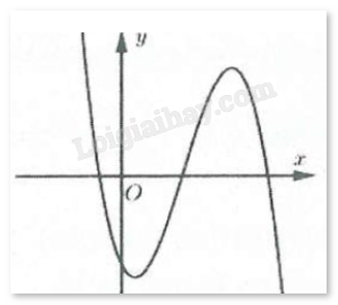
a < 0, b < 0, c > 0, d < 0
a > 0, b > 0, c < 0, d < 0
a < 0, b < 0, c < 0, d > 0
a < 0, b > 0, c < 0, d < 0
Câu 10 : Cho hàm số y = f(x) xác định và liên tục trên R và có đô thị của đạo hàm y = f’(x) như hình bên dưới. Chọn phát biểu đúng khi nói về hàm số y = f(x).
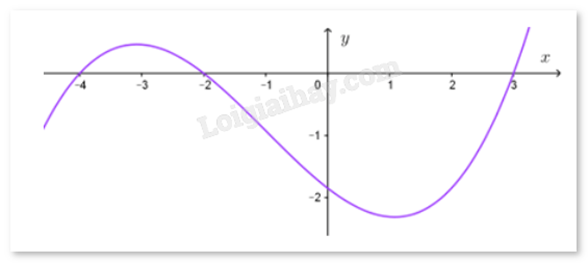
Hàm số y = f(x) có hai điểm cực trị
Hàm số nghịch biến trên khoảng (-3;0)
f(0) > f(3)
và
Câu 11 : Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto và ?
Câu 12 : Cho hai vecto thỏa mãn , , . Gọi là góc giữa hai vecto . Chọn khẳng định đúng?
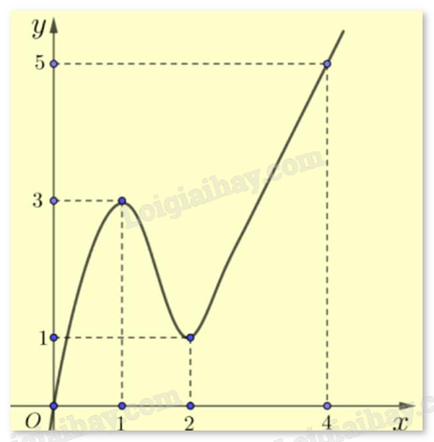
Cho hàm số f(x) xác định trên R có đồ thị như sau:
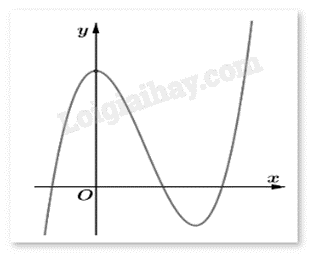
a) Đồ thị hàm số đã cho có hai cực trị
b) Hàm số đã cho đồng biến trên R
c) Hàm số không có giá trị lớn nhất và nhỏ nhất
d) Đồ thị hàm số f(x) là
Cho đồ thị của hàm số f(x) như sau:
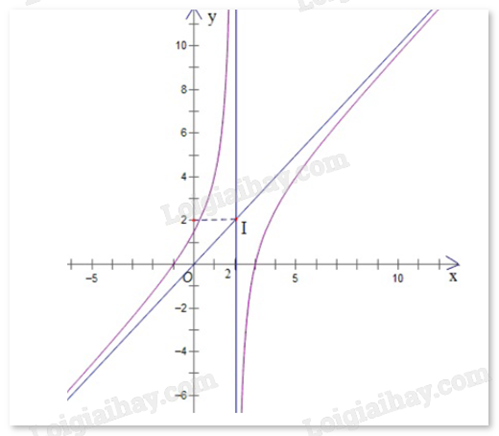
a) Đồ thị hàm số f(x) là đồ thị của hàm số
b) Đồ thị hàm số nhận giao điểm I(2;2) của hai đường tiệm cận làm tâm đối xứng
c) Hàm số f(x) đồng biến trên mỗi khoảng và
d) Hàm số y = f(x) có hai cực trị
Cho hình hộp ABCD.A’B’C’D’ tâm O.
a)
b)
c)
d)
Trong không gian Oxyz, biết vuông góc vối cả hai vecto , .
a)
b)
c)
d)
Tìm giá trị nhỏ nhất của hàm số .
Đáp án:
Với giá trị nào của tham số m để đồ thị hàm số có tiệm cận đứng đi qua điểm A(1;3)?
Đáp án:
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(-3;0;0), B(0;2;0), D(0;0;1), A’(1;2;3). Tính tổng của hoành độ, tung độ, cao độ đỉnh C’.
Đáp án:
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc của cá bơi khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức , trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Đáp án:
Tìm tất cả các giá trị của tham số m để hàm số đạt cực tiểu tại x = 2.
Đáp án:
Cho hàm số có đồ thị như hình:
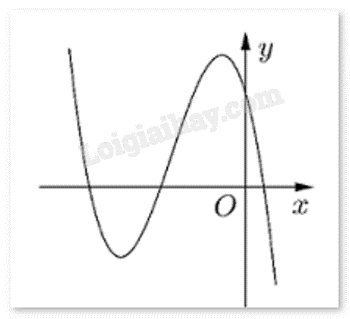
Có bao nhiêu số dương trong các số a, b, c, d?
Đáp án:
ĐÁP ÁN
| 1. A | 2. D | 3. C | 4. D | 5. A | 6. B |
| 7. B | 8. D | 9. D | 10. C | 11. C | 12. A |
a) Đúng. Hàm số f(x) có hai cực trị.
b) Sai. Hàm số có khoảng nghịch biến.
c) Đúng. Hàm số không có giá trị lớn nhất và nhỏ nhất.
d) Sai. Đồ thị có dạng của hàm số bậc 3.
a) Sai. Đồ thị có tiệm cận đứng là x = 1. Tiệm cận đứng của đồ thị trên hinh là x = 2.
b) Đúng. Đồ thị hàm số nhận giao điểm I(2;2) của hai đường tiệm cận làm tâm đối xứng.
c) Đúng. Hàm số f(x) đồng biến trên mỗi khoảng và .
d) Sai. Hàm số không có cực trị.
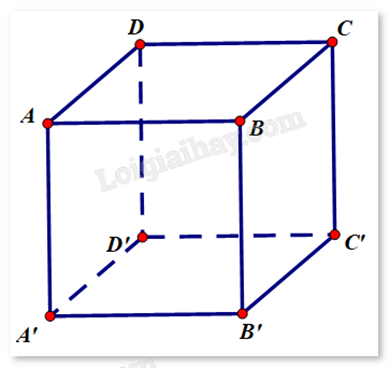
a) Sai. , , mà nên sai.
b) Đúng. Theo quy tắc hình hộp: .
c) Đúng. .
d) Đúng. , , suy ra .
a) Sai. Vì .
b) Sai. Vì .
c) Đúng. Vì .
d) Đúng. Theo giả thiết ta có và vuông góc với cả hai vecto và nên
Đặt , khi đó .
Ta có: .
Suy ra hàm f(t) đồng biến trên (-1;1), do đó giá trị nhỏ nhất của hàm số là f(-1) = 1.
Tiệm cận đứng của đồ thị hàm số là .
Tiệm cận đứng của đồ thị hàm số đi qua điểm A(1;3) nên .
Thử lại thấy thỏa mãn.
Gọi C’(x;y;z). Ta có: , , .
Mà , suy ra .
Ta có: , vậy C’(13;4;4).
Vậy tổng cần tìm là 13 + 4 + 4 = 21.
Vận tốc cá bơi khi ngược dòng là v – 6 (km/h). Thời gian cá bơi để vượt khoảng cách 300 km là (giờ).
Năng lương tiêu hao của cá để vượt khoảng cách đó là (jun), v > 6.
Ta có:
Loại v = 0 vì v > 6.
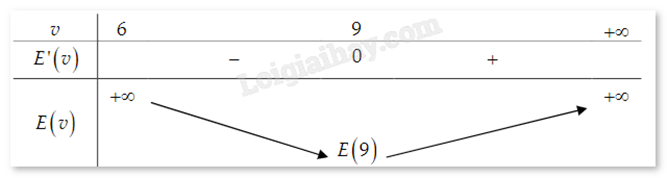
Dựa vào bảng biến thiên, ta thấy để tiêu hao ít năng lượng nhất, cá phải bơi với vận tốc (khi nước đứng yên) là 9 (km/h).
Ta có: ,
Hàm số đạt cực tiêu tại x = 2 khi và chỉ khi .
Ta thấy nên a < 0.
Đồ thị cắt trục Oy tại điểm có tung độ dương nên d > 0.
Ta có: . Hàm số đạt cực trị tại hai điểm nên:
(do a < 0)
Vậy có 1 số dương d.
Đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 2
Sở Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Kết nối tri thức
Năm học ...............
Môn: Toán lớp 12
Thời gian làm bài: phút
(Đề số 2)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (-∞;0).
B. (-∞;2).
C. (0;0).
D. (0;+∞).
Câu 2. Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình dưới đây.
Phát biểu nào sau đây là đúng?
A. xCT = -1, xCĐ = 1.
B. xCT = -1, xCĐ = 3.
C. xCT = 3, xCĐ = -1.
D. xCT = 1, xCĐ = -1.
Câu 3. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
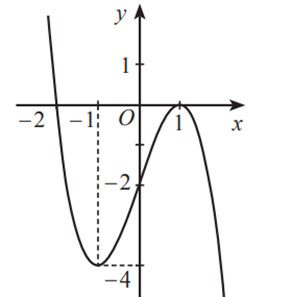
Giá trị nhỏ nhất của hàm số đã cho trên đoạn [-2;0] là:
A. -1.
B. -4.
C. -2.
D. 1.
Câu 4. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận đứng x = 2, đường tiệm cận ngang y = -1.
B. Đồ thị hàm số có đường tiệm cận đứng x = -1, đường tiệm cận ngang y = 2.
C. Đồ thị hàm số có đường tiệm cận đứng x = -1, đường tiệm cận ngang y = -1.
D. Đồ thị hàm số có đường tiệm cận đứng x = 2, đường tiệm cận ngang y = 0.
Câu 5. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng
A. y = x - 1.
B. y = -x - 1.
C. y = x + 1.
D. y = -x + 1.
Câu 6. Cho hàm số y = f(x) có đồ thị như hình dưới đây.
Tâm đối xứng của đồ thị hàm số có tọa độ là
A. (1;0).
B. (-1;1).
C. (2;-2).
D. (1;-1).
Câu 7. Phát biểu nào sau đây là đúng?
A. Với hai vectơ bất kì và số thực k, ta có .
B. Với hai vectơ bất kì và số thực k, ta có .
C. Với hai vectơ bất kì và số thực k, ta có .
D. Với hai vectơ bất kì và số thực k, ta có .
Câu 8. Hàm số nào sau đây nghịch biến trên ℝ?
A. .
B. y = -x3 - 3x - 2024.
C. y = -x3 - 2x2 + x + 2024.
D. 2x2 - 3x + 2024.
Câu 9. Giá trị lớn nhất của hàm số y = (x - 3)2 . ex trên đoạn [2;4] bằng
A. 0.
B. 4e.
C. e2.
D. e4.
Câu 10. Quan sát bảng biến thiên và cho biết bảng biến thiên đó là của hàm số nào.
A. .
B. .
C. .
D. .
Câu 11. Cho hàm số có đồ thị như hình vẽ.
Trong các số a,b,c,d có bao nhiêu số có giá trị dương?
A. 1.
B. 2.
C. 3.
D. 4.
Câu 12. Cho tứ diện đều ABCD có cạnh bằng a. Tích vô hướng bằng
A. a2.
B. -a2.
C. a2.
D. a2.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y = f(x) xác định trên ℝ và có bảng biến thiên như sau:
a) Hàm số y = f(x) đồng biến trên mỗi khoảng (-∞;1) và (3;+∞).
b) Số điểm cực trị của hàm số đã cho là 3.
c) Hàm số y = f(x) có giá trị nhỏ nhất bằng 0.
d) Đồ thị hàm số không có đường tiệm cận.
Câu 2. Cho hàm số y = ex - x + 3.
a) Hàm số đã cho nghịch biến trên ℝ.
b) Hàm số đã cho đạt cực đại tại x = 0.
c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ là (0;4).
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ.
Câu 3. Cho hình hộp ABCD.A'B'C'D'.
a) Các vectơ bằng với vectơ là .
b) Các vectơ đối của vectơ là .
c) .
d) .
Câu 4. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = AC = AD = 1. Gọi M là trung điểm của BC.
a) .
b) .
c) .
d) .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Giả sử hàm số đạt cực đại tại x = a và đạt cực tiểu tại x = b. Giá trị của biểu thức M = 2a - 3b bằng bao nhiêu?
Câu 2. Cho hàm số y = ex+2 + 5x - m với m là tham số thực. Với giá trị nào của m thì hàm số đã cho có giá trị lớn nhất trên đoạn [0;3] bằng e5?
Câu 3. Cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm của A'D' và C'D'. Gọi φ là góc giữa hai vectơ và . Số đo của góc φ bằng bao nhiêu độ?
Câu 4. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
Câu 5. Cho hàm số có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận của (C), M là một điểm bất kì trên (C) và tiếp tuyến của (C) tại M cắt hai tiệm cận tại A, B. Biết chu vi tam giác IAB có giá trị nhỏ nhất bằng với a,b ∈ ℕ. Giá trị của biểu thức a - b + 4 bằng bao nhiêu?
Câu 6. Có ba lực cùng tác động vào một cái bàn như hình vẽ dưới. Trong đó hai lực tạo với nhau một góc 110° và có độ lớn lần lượt là 9 N và 4 N, lực vuông góc với mặt phẳng tạo bởi hai lực và có độ lớn 7 N. Độ lớn hợp lực của ba lực trên là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị của Newton)?