Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 9 sách Chân trời sáng tạo năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Học kì 1 Toán 9. Mời các bạn cùng đón xem:
Đề thi học kì 1 Toán 9 Chân trời sáng tạo có đáp án năm 2025
Đề thi học kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 9
Thời gian làm bài: phút
(Đề số 1)
Câu 1 : Cho hệ phương trình . Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
.
.
.
.
Câu 2 : Điều kiện xác định của phương trình
và .
và .
và .
và .
Câu 3 : Số 3 là nghiệm của bất phương trình nào sau đây?
.
.
.
.
Câu 4 : Số nào sau đây có căn bậc hai số học bằng 4?
2.
4.
-2.
16.
Câu 5 : Căn thức xác định khi
.
.
.
.
Câu 6 : Sau khi rút gọn biểu thức ta được phân số tối giản , giá trị là
10.
9.
8.
7.
Câu 7 : Giá trị của biểu thức là
12.
15.
18.
21.
Câu 8 : Tam giác ABC vuông tại A có AC = 6cm; BC = 12cm. Số đo góc ACB bằng
.
.
.
.
Câu 9 : Dây lớn nhất của đường tròn có độ dài bằng
8cm.
6cm.
4cm.
3cm.
Câu 10 : Cho hình vẽ. Chọn khẳng định đúng.
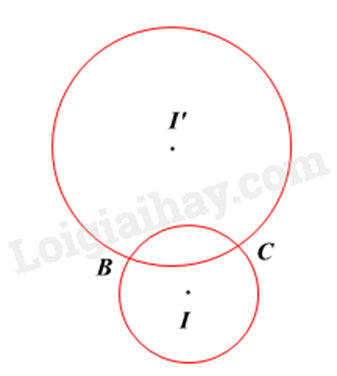
Hai đường tròn và tiếp xúc trong.
Hai đường tròn và tiếp xúc ngoài.
Hai đường tròn và cắt nhau.
Hai đường tròn và không giao nhau.
Câu 11 : Tỉ số giữa độ dài cung và độ dài đường tròn (cùng bán kính) bằng
.
.
.
.
Câu 12 : Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Khi đó
AC là tiếp tuyến của đường tròn (B; 3).
AC là tiếp tuyến của đường tròn (C; 4).
BC là tiếp tuyến của đường tròn (A; 3).
AB là tiếp tuyến của đường tròn (C; 3).
Câu 1 : Cho biểu thức và
a) Rút gọn P.
b) Tính giá trị của P khi .
c) Biết . Tìm giá trị của x để .
Câu 2 : Bác An chia số tiền triệu đồng của mình cho hai khoản đầu tư. Sau một năm lợi nhuận thu về là triệu đồng. Lợi nhuận của khoản đầu tư thứ nhất là , lợi nhuận của khoản đầu tư thứ hai là . Tính số tiền bác An đầu tư cho mỗi khoản?
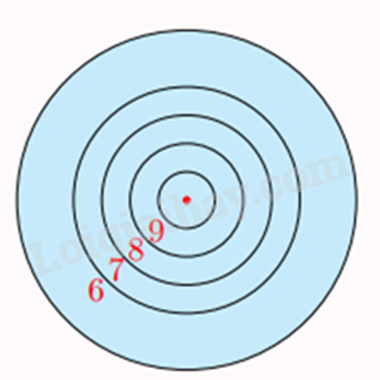
Câu 3 : Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính , , , và . Giả thiết rằng người chơi ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 9 (hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai). Biết rằng xác suất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
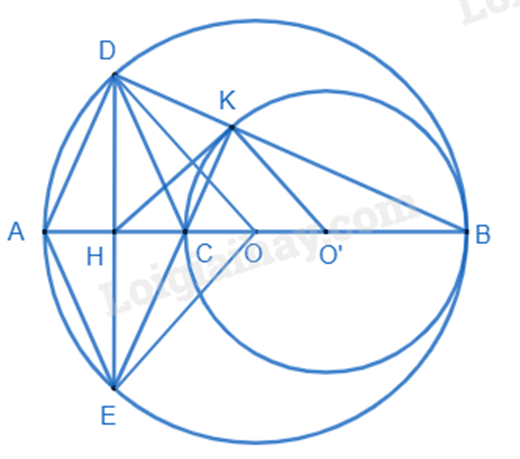
Câu 4 : Cho đường tròn , đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn có đường kính CB.
a) Kẻ dây DE của đường tròn vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
b) Gọi K là giao điểm của DB và đường tròn . Chứng minh rằng ba điểm E, C, K thẳng hàng;
c) Chứng minh HK là tiếp tuyến của đường tròn .
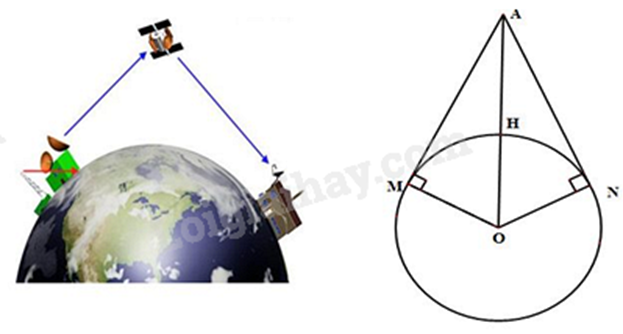
Câu 5 : Vinasat-1 là vệ tinh viễn thông địa tĩnh đầu tiên của Việt Nam được phóng vào vũ trụ lúc 22 giờ 17 phút ngày 18 tháng 4 năm 2008 (giờ UTC). Dự án vệ tinh Vinasat-1 đã khởi động từ năm 1998 với tổng mức đầu tư là khoảng hơn 300 triệu USD. Việt Nam đã tiến hành đàm phán với 27 quốc gia và vùng lãnh thổ để có được vị trí 132 độ Đông trên quỹ đạo địa tĩnh.
Hãy tìm khoảng cách từ vệ tinh Vinasat-1 đến mặt đất. Biết rằng khi vệ tinh phát tín hiệu vô tuyến đến một điểm xa nhất trên mặt đất thì từ lúc phát tín hiệu đến mặt đất cho đến lúc vệ tinh thu lại được tín hiệu phản hồi mất khoảng thời gian là 0,28s. Trái đất được xem như một hình cầu có bán kính khoảng 6400km (ghi kết quả gần đúng chính xác đến hàng đơn vị), giả sử vận tốc sóng vô tuyến là m/s.
ĐÁP ÁN
| 1C | 2C | 3B | 4D | 5B | 6B |
| 7C | 8C | 9B | 10C | 11A | 12A |
Câu 1 :
a) Ta có:
.
b) Thay vào P, ta được:
.
Vậy với thì .
c) Ta có:
Vì nên . Suy ra
Vì nên
Do đó
Kết hợp điều kiện ta được .
Vậy để thì .
Câu 2 :
Gọi số tiền đầu tư cho mỗi khoản lần lượt là ( )
Vì bác An chia số tiền triệu đồng của mình cho hai khoản đầu tư nên (triệu đồng)
Vì lợi nhuận của khoản đầu tư thứ nhất là , lợi nhuận của khoản đầu tư thứ hai là và sau một năm lợi nhuận thu về là triệu đồng nên hay
Ta có hệ phương trình
Giải hệ phương trình:
Vậy khoản đầu tư thứ nhất là triệu đồng, khoản đầu tư thứ hai là triệu đồng.
Câu 3 :
Vì bán kính của đường tròn thứ nhất và thứ hai lần lượt là 5cm và 10cm nên diện tích hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai là:
Vì hình tròn lớn nhất có bán kính là 30cm nên diện tích hình tròn lớn nhất:
Xác suất ném trúng vòng 8 là:
Vậy xác suất ném trúng vòng 9 là .
Câu 4 :
a) Xét và có:
Suy ra
Do đó DH = HE (hai cạnh tương ứng).
Mà suy ra H là trung điểm của BE.
Tứ giác ADCE có H là trung điểm của hai đường chéo DE, AC và tại H nên tứ giác ADCE là hình thoi.
b) Ta có (Vì AB là đường kính của và ) nên suy ra (1) (Vì tứ giác ADCE là hình thoi).
Lại có (Vì CB là đường kính của và ) hay (2).
Từ (1) và (2) suy ra E, C, K thẳng hàng (tiên đề Euclid).
c) Xét vuông tại K có KH là đường trung tuyến ứng với cạnh huyền nên .
Suy ra cân tại H, do đó .
Lại có (tam giác O’CK cân tại O’) và (2 góc đối đỉnh) do đó .
Mà (hai góc phụ nhau) nên , suy ra
Do đó .
Vậy HK là tiếp tuyến của tại K .
Câu 5 :
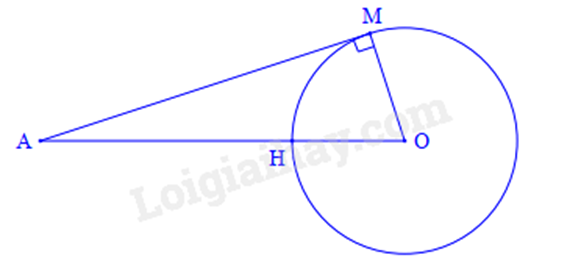
Do thời gian từ lúc truyền tín hiệu đến lúc nhận lại tín hiệu là 0,28s, nên thời gian tín hiệu truyền từ A đến M là:
Độ dài đoạn AM cũng là quãng đường tín hiệu truyền đi được trong 0,14s là:
Vị trí xa nhất trên trái đất có thể nhận tín hiệu từ vệ tinh là vô số điểm M (với AM là tiếp tuyến kẻ từ A đến đường tròn tâm O).
Vì AM là tiếp tuyến (O) nên tại M.
Áp dụng định lý Pythagore vào tam giác vuông AMO ta có:
Suy ra .
Khoảng cách từ vệ tinh Vinasat-1 đến mặt đất là độ dài đoạn AH:
.
Đề thi học kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 9
Thời gian làm bài: phút
(Đề số 2)
I. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Điều kiện xác định của phương trình là
A. x ≠ 2.
B. x ≠ 3.
C. x ≠ –2; x ≠ 3.
D. x ≠ –3; x ≠ 2.
Câu 2. Nghiệm của hệ phương trình là
A. (2; 1).
B. (1; 2).
C. (–1; 7).
D. (–1; 0).
Câu 3. Cho a bất kỳ. Mệnh đề nào dưới đây là đúng?
A. 2a – 7 > 2a – 5.
B. 2a – 3 > 2a – 2.
C. 3a – 4 > 3a – 6.
D. 2a – 4 > 2a – 5.
Câu 4. Bất phương trình 2 + 5x ≥ –1 – x có tập nghiệm là
A. .
B. .
C. .
D. .
Câu 5. Biểu thức nào sau đây có điều kiện xác định là x ≥ 0, x ≠ 9?
A. .
B. .
C. .
D. .
Câu 6. Điều kiện xác định của là
A. x < 9.
B. x > 9.
C. x ≥ 9.
D. x ≤ 9.
Câu 7. Kết quả của phép tính với a ≥ 0 là
A. .
B. .
C. .
D. .
Câu 8. Cho tam giác MNP vuông tại M. Khi đó, bằng
A. .
B. .
C. .
D. .
Câu 9. Cho tam giác ABC vuông tại A có và AB = 8 cm. Độ dài cạnh BC bằng
A. 4 cm.
B. cm.
C. cm.
D. 16 cm.
Câu 10. Cho hai đường tròn (O; R) và (O'; R') thỏa mãn R - R' < OO' < R + R'. Số điểm chung của hai đường tròn là
A. 0.
B. 1.
C. 2.
D. 3.
Câu 11. Biết độ dài cung 60° là 6π. Độ dài cung tròn có số đo 100° là
A. 6π.
B. .
C. 9π.
D. 10π.
Câu 12. Cho hai đường tròn (O; 2 cm) và (O'; 5 cm) tiếp xúc ngoài thì độ dài của OO' bằng
A. 2 cm.
B. 7 cm.
C. 3 cm.
D. 1 cm.
II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Cho hai biểu thức: A = và B = với x > 0, x ≠ 9.
a) Tính giá trị của biểu thức A với x = .
b) Rút gọn biểu thức B.
c) Biết P = , tính giá trị lớn nhất của P.
Bài 2. (2,0 điểm)
1. Giải các phương trình, bất phương trình sau:
a) .
b) (x - 4)(x + 4) + 2x(x - 4) ≥ 3x2.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Lan có một dung dịch nước muối sinh lí có nồng độ 1,5% và một dung dịch nước cất không chứa muối (nồng độ 0%). Lan cần pha trộn dung dịch này thu được 1 lít (1000 ml) dung dịch nước muối dinh lí súc miệng có nồng độ 0,9%. Hỏi cần bao nhiêu ml dung dịch nước muối và bao nhiêu ml nước cất để tạo ra dung dịch mong muốn?
|
Bài 3. (1,0 điểm) Một người quan sát một tòa nhà và đứng cách tòa nhà khoảng 25 m. Góc nâng từ mắt người quan sát đến nóc tòa nhà là 36°. |
|
a) Viết tỉ số lượng giác tan 36° trong tình huống này.
b) Nếu anh ta đi thêm 5 m nữa, đến vị trí E nằm giữa C và H, thì góc nâng từ F đến nóc tòa nhà là bao nhiêu (làm tròn đến độ)? Biết chiều cao CD tính từ chân đến mắt người quan sát là 1,6 m.
Bài 4. (2,0 điểm) Cho ∆ABC nhọn có ba đỉnh nằm trên đường tròn (O). Điểm M di động trên cung nhỏ BC. Vẽ MH vuông góc với AB ở H, MK vuông góc với AC ở K.
a) Chứng minh rằng AM là đường kính của đường tròn đi qua ba điểm A, H, K.
b) Chứng minh rằng HK =
c) Xác định vị trí của điểm M trên cung nhỏ BC để HK dài nhất.
|
Bài 5. (0,5 điểm) Nam làm một chiếc hộp không nắp dạng hình hộp chữ nhật bằng bìa carton có thể tích 3 dm3. Biết tỉ số giữa chiều cao h và chiều rộng đáy y bằng 4. Xác định chiều dài x để lượng bìa cần sử dụng là ít nhất. |
|
-----HẾT-----
ĐÁP ÁN & HƯỚNG DẪN
I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
C |
A |
D |
B |
A |
D |
B |
B |
D |
C |
D |
B |
II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
Hướng dẫn giải
a) Thay (thỏa mãn điều kiện) vào biểu thức A, ta được:
A = .
Vậy giá trị của biểu thức khi .
b) Với x > 0, x ≠ 9, ta có:
B =
=
= .
Vậy với x > 0, x ≠ 9 thì B = .
c) Ta có: P =
=
= .
Với x > 0, x ≠ 9, thì P = .
d) Với x > 0, x ≠ 9, ta có:
P = = = = .
Áp dụng bất đẳng thức Cauchy cho các số dương và , ta có:
Dấu “=” xảy ra khi , tức là nên (do ) hay x = 1 (thỏa mãn).
Vậy giá trị lớn nhất của P = 1 khi x = 1.
Bài 2. (2,0 điểm)
Hướng dẫn giải
2. Gọi x (ml) là thể tích dung dịch nước muối 1,5% và y là thể tích nước cất 0% (x, y > 0).
Tổng thể tích dung dịch là 1 000 ml nên ta có phương trình x + y = 1000 (1)
Tổng khối lượng muối trong dung dịch là 0,9% của 1 000 ml. Lượng muối trong dung dịch ban đầu là 1,5%x và trong nước cất là 0.
Do đó: 0,015x + 0y = 0,009 . 1000 hay 0,015x = 9 (2).
Từ (1) và (2) ta có hệ phương trình: .
Giải phương trình 0,015x = 9 được x = 9 : 0,015 = 600 (thỏa mãn).
Thay x = 600 vào phương trình (1), được: y = 1000 – 600 = 400 (thỏa mãn).
Vậy Lan cần 600 ml dung dịch nước muối 1,5% và 400 ml dung dịch nước cốt 0% để pha được dung dịch mong muốn.
Bài 3. (1,0 điểm)
Hướng dẫn giải
a) Xét ∆AKD vuông tại D, ta có: .
b) Ta có: FK = EH = CH – CE = 25 – 5 = 20 (m).
Từ ta có AK = KD.tan36° = 25.tan36° ≈ 18,164 (m).
Ta có AH = AK + KH ≈ 18,164 + 1,6 = 19,764 ≈ 20 (m).
Xét ∆AFK vuông tại K, ta có: , do đó .
Vậy góc nâng từ F đến nóc tòa nhà khoảng 42°.
Bài 4. (2,0 điểm)
Hướng dẫn giải
a) Gọi I là trung điểm của AM. Khi đó AI = MI = AM.
Xét ∆AHM vuông tại H có HI là đường trung tuyến ứng với cạnh huyền AM nên HI = AM.
Xét ∆AKM vuông tại K có KI là đường trung tuyến ứng với cạnh huyền AM nên KI = AM.
Do đó AI = HI = MI = KI = AM nên bốn điểm A, H, M, K cùng thuộc đường tròn tâm I, đường kính AM.
Hay AM là đường kính của đường tròn (I) đi qua ba điểm A, H, K.
b) Gọi N là giao điểm của HI và đường tròn tâm I đường kính AM
Suy ra (góc nội tiếp chắn nửa đường tròn) hay ∆HKN vuông tại K)
Ta có HK =
Mà HN = AM (cùng là đường kính của đường tròn tâm I)
Và (hai góc nội tiếp cùng chắn cung HK của đường tròn tâm I)
Suy ra HK = .
c) Ta có ∆ABC cố định nên không đổi.
Do đó từ HK = , để HK dài nhất thì AM dài nhất mà AM là dây của đường tròn (O).
Nên AM dài nhất khi AM là đường kính của đường tròn (O).
Do đó M đối xứng với A qua (O).
Bài 5. (0,5 điểm)
Hướng dẫn giải
Theo đề bài, tỉ số giữa chiều cao h và chiều rộng đáy y bằng 4 nên h = 4y.
Thể tích chiếc hộp 3 dm3 nên xyh = 3 (dm3) hay 4xy2 = 3, suy ra x = .
Do chiếc hộp không nắp, do đó diện tích bìa cần dùng là tổng diện tích đáy hộp và diện tích xung quanh của hộp.
Ta có: S = xy + 2h(x + y) =
= = =
Do y là chiều rộng của hộp nên y > 0.
Do đó, áp dụng bất đẳng thức Cauchy cho ba số không âm, ta được:
, suy ra .
Dấu “=” xảy ra khi và chỉ khi , hay nên (dm).
Do đó, x = (dm).
Vậy lượng bìa cần dùng ít nhất có diện tích là dm2 khi chiều dài x = dm
-----HẾT-----