Bộ 10 đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án năm 2024

Thuy Quynh Ngày: 11-01-2025 Lớp 9

1.4 K

Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 9 sách Chân trời sáng tạo năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 9. Mời các bạn cùng đón xem:

Đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án năm 2024

Đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Chân trời sáng tạo

Năm học 2024 - 2025

Môn: Toán lớp 9

Thời gian làm bài: phút

(Đề số 1)

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 : Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?

A.

$2 x + 3 y = 5$ .
B.

$0 x + 2 y = 8$ .
C.

$2 x - 0 y = 5$ .
D.

$0 x - 0 y = 6$ .

Câu 2 : Hệ phương trình ${\begin{cases} 2 x + y = 2 \\ x + y = 1 \end{cases}$ có nghiệm là:

A.

$(x; y) = (0; 0)$ .
B.

$(x; y) = (1; 0)$ .
C.

$(x; y) = (1; 1)$ .
D.

$(x; y) = (- 1; - 1)$ .

Câu 3 : Người ta cần chở một số lượng hàng. Nếu xếp vào mỗi xe 12 tấn thì thừa 3 tấn, nếu xếp vào mỗi xe 15 tấn thì có thể chở thêm 12 tấn nữa. Gọi x là số hàng cần vận chuyển và y là số xe tham gia chở hàng. Hệ phương trình thỏa mãn là:

A.

${\begin{cases} x + 12 y = 3 \\ x - 15 y = 12 \end{cases}$ .
B.

${\begin{cases} x - 12 y = 3 \\ - x + 15 y = 12 \end{cases}$ .
C.

${\begin{cases} x - 12 y = 3 \\ x + 15 y = 12 \end{cases}$ .
D.

${\begin{cases} x + 12 y = 3 \\ - x + 15 y = 12 \end{cases}$ .

Câu 4 : Biến đổi phương trình $x^{2} - 4 x + 3 = 0$ về phương trình tích, ta được:

A.

$(x + 1) (x - 3) = 0$ .
B.

$(x + 1) (x + 3) = 0$ .
C.

$(x - 1) (x - 3) = 0$ .
D.

$(x - 1) (x + 3) = 0$ .

Câu 5 : Hệ thức $2 a \leq a + 1$ là một bất đẳng thức và

A.

$a + 1$ là vế trái, $2 a$ là vế phải.
B.

$a + 1$ là vế trước, $2 a$ là vế sau.
C.

$a + 1$ là vế sau, $2 a$ là vế trước.
D.

$2 a$ là vế trái, $a + 1$ là vế phải.

Câu 6 : Khẳng định nào sau đây là khẳng định đúng:

A.

$a < b$ và $c > d$ thì $a + b < c + d$ .
B.

$a < b$ và $c < d$ thì $a + c < b + d$ .
C.

$a > b$ và $c > d$ thì $a c > b d$ .
D.

$a > b$ và $c > d$ thì $a + c < b + d$ .

Câu 7 : Bất phương trình dạng $a x + b > 0$ (hoặc $a x + b < 0$ , $a x + b \geq 0$ , $a x + b \leq 0$ ) là bất phương trình bậc nhất một ẩn (ẩn là $x$ ) với điều kiện:

A.

a, b là hai số đã cho.
B.

a, b là hai số đã cho và $a \neq 0$ .
C.

$a \neq 0$ .
D.

a và b khác 0.

Câu 8 : Nghiệm của bất phương trình $x - 2 > 0$ là:

A.

$x > 2$ .
B.

$x < 2$ .
C.

$x < - 2$ .
D.

$x > - 2$ .

Câu 9 : Cho $α$ và $β$ là hai góc phụ nhau, khi đó:

A.

$\sin α = \cos β$ .
B.

$\sin α = \cot β$ .
C.

$\sin α = \tan β$ .
D.

$\cos α = \cot β$ .

Câu 10 : Cho $α$ là góc nhọn bất kì có $\tan α = \frac{1}{5}$ , khi đó $\cot α$ bằng:

A.

$\frac{1}{5}$ .
B.

$- \frac{1}{5}$ .
C.

$5$ .
D.

$- 5$ .

Câu 11 : Cho tam giác ABC vuông tại B có $\hat{A} = 45^{\circ}$ , $A C = \sqrt{2}$ . Độ dài cạnh BC là:

A.

$B C = 3$ .
B.

$B C = 2$ .
C.

$B C = \sqrt{2}$ .
D.

$B C = 1$ .

Câu 12 : Cho tam giác ABC vuông tại A có AB = 5, BC = 8. Số đo góc C là: (làm tròn đến độ)

A.

$\hat{C} \approx 52^{\circ}$ .
B.

$\hat{C} \approx 38^{\circ}$ .
C.

$\hat{C} \approx 51^{\circ}$ .
D.

$\hat{C} \approx 39^{\circ}$ .

II. Tự luận

Câu 1 : Giải các phương trình và bất phương trình sau:

a) $(x - 1) (3 x - 6) = 0$

b) $\frac{2}{x + 3} - \frac{1}{x - 2} = \frac{2 x - 13}{(x + 3) (x - 2)}$

c) $2 x - 4 > 0$

d) $2 - 3 x \leq 4 x + 5$

Câu 2 : a) Giải hệ phương trình: ${\begin{cases} 3 x - 2 y = 5 \\ 2 x + y = 1 \end{cases}$ .

b) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 công cụ. Nhờ sắp xếp hợp lý dấy chuyền sản xuất nên xí nghiệp I đã vượt mức 12% kế hoạch, xí nghiệp II đã vượt mức 10% kế hoạch. Do đó cả xí nghiệp đã làm được 400 công cụ. Tính số công cụ mỗi xí nghiệp phải làm theo kế hoạch.

Câu 3 : Tượng đài chiến thắng là một công trình kiến trúc độc đáo được thi công nhằm kỷ niệm ngày giải phóng thị xã Long Khánh, ngày 21/04/1975 – thể hiện ý chí quyết thắng của quân và dân ta. Em hãy tính chiều cao của công trình này biết rằng khi tia nắng của mặt trời tạo với mặt đất một góc $52^{\circ}$ thì bóng của nó trên mặt đất là 16m. (Làm tròn đến số thập phân thứ hai). (Giả sử chu vi mặt đáy khối chóp tam giác không đáng kể)

Bộ 10 đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án năm 2024 (ảnh 1)

Câu 4 : Cho tam giác ABC vuông tại A, đường cao AH.

a) Biết $A B = 2 \sqrt{3} c m$ ; $A C = 6 c m$ . Giải tam giác ABC.

b) Gọi D, E lần lượt là hình chiếu của điểm H trên AB, AC. Chứng minh $B D . D A + C E . E A = A H^{2}$ .

c) Lấy điểm M nằm giữa E và C, kẻ AI vuông góc với MB tại I.

Chứng minh $\sin \hat{A M B} . \sin \hat{A C B} = \frac{H I}{C M}$ .

Câu 5 : Một lão nông chia đất cho con trai để người con canh tác riêng, biết rằng người con sẽ được chọn miếng đất hình chữ nhật có chu vi 800 m. Hỏi anh ta phải chọn mảnh đất có kích thước như thế nào để diện tích đất canh tác là lớn nhất.

(HD: Sử dụng bất đẳng thức $a b \leq \frac{{(a + b)}^{2}}{4}$ ).

ĐÁP ÁN

I. Trắc nghiệm

1. D	2. B	3. B	4. C	5. D	6. B
7. B	8. A	9. A	10. C	11. D	12. D

II. Tự luận

Câu 1:

a) $(x - 1) (3 x - 6) = 0$

+) $x - 1 = 0$

$x = 1$

+) $3 x - 6 = 0 x = 1$

$3 x = 6$

$x = 2$

Vậy phương trình có nghiệm là $x = 1$ ; $x = 2$ .

b) $\frac{2}{x + 3} - \frac{1}{x - 2} = \frac{2 x - 13}{(x + 3) (x - 2)}$

ĐKXĐ: $x \neq - 3$ và $x \neq 2$ .

Ta có:

$\begin{array}{l} \frac{2}{x + 3} - \frac{1}{x - 2} = \frac{2 x - 13}{(x + 3) (x - 2)} \frac{2}{x + 3} - \frac{1}{x - 2} = \frac{2 x - 13}{(x + 3) (x - 2)} \\ \frac{2 (x - 2)}{(x + 3) (x - 2)} - \frac{x + 3}{(x + 3) (x - 2)} = \frac{2 x - 13}{(x + 3) (x - 2)} \\ 2 (x - 2) - (x + 3) = 2 x - 13 \\ 2 x - 4 - x - 3 = 2 x - 13 \\ x - 7 = 2 x - 13 \\ x - 2 x = - 13 + 7 \\ - x = - 6 \\ x = 6 (T M) \end{array}$

Vậy phương trình có nghiệm là $x = 6$ .

c) $2 x - 4 > 0$

$\begin{array}{l} 2 x > 4 \\ x > 2 \end{array}$

Vậy bất phương trình có nghiệm là $x > 2$ .

d) $2 - 3 x \leq 4 x + 5$

$\begin{array}{l} - 3 x - 4 x \leq 5 - 2 \\ - 7 x \leq 3 \\ x \geq \frac{- 3}{7} \end{array}$

Vậy bất phương trình có nghiệm là $x \geq \frac{- 3}{7}$ .

Câu 2:

a) Ta có:

$\begin{array}{l} {\begin{cases} 3 x - 2 y = 5 \\ 2 x + y = 1 \end{cases} \\ {\begin{cases} 3 x - 2 y = 5 \\ 4 x + 2 y = 2 \end{cases} \\ {\begin{cases} 7 x = 7 \\ 2 x + y = 1 \end{cases} \\ {\begin{cases} x = 1 \\ 2.1 + y = 1 \end{cases} \\ {\begin{cases} x = 1 \\ y = - 1 \end{cases} \end{array}$

Vậy hệ phương trình có nghiệm là $(x; y) = (1; - 1)$ .

b) Gọi số dụng cụ mà xí nghiệp 1 và xí nghiệp II phải làm lần lượt là $x, y$ $(x, y \in N^{*})$ .

Theo kế hoạch, hai xí nghiệp sản xuất phải làm tổng cộng 360 dụng cụ nên ta có:

$x + y = 360$ (1)

Thực tế, xí nghiệp I đã vượt mức 12% kế hoạch, xí nghiệp II đã vượt mức 10% kế hoạch, do đó hai xí nghiệp đã làm được 400 dụng cụ nên ta có phương trình:

$(x + 12 % x) + (y + 10 % y) = 400$ hay $1, 12 x + 1, 1 y = 400$ (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{cases} x + y = 360 \\ 1, 12 x + 1, 1 y = 400 \end{cases}$ .

Giải hệ phương trình ta được: ${\begin{cases} x = 200 \\ y = 160 \end{cases} (T M)$ .

Vậy theo kế hoạch xí nghiệp I làm được 200 dụng cụ và xí nghiệp II làm được 160 dụng cụ.

Câu 3:

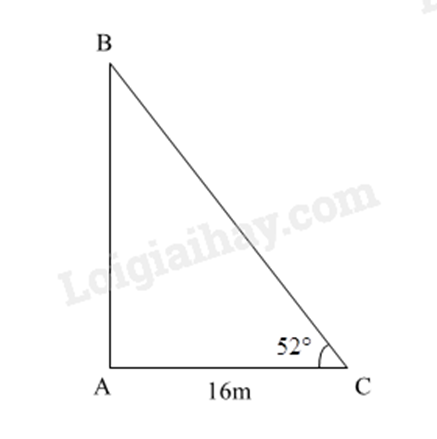
Bộ 10 đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án năm 2024 (ảnh 2)

Giả sử hình biểu diễn như hình vẽ.

Xét tam giác ABC vuông tại A, ta có: $\tan B C A = \frac{A B}{A C}$

Suy ra $A B = A C . \tan B C A = 16. \tan 52^{\circ} \approx 20, 48 (m)$

Vậy chiều cao của công trình này là khoảng $20, 48 m$ .

Câu 4:

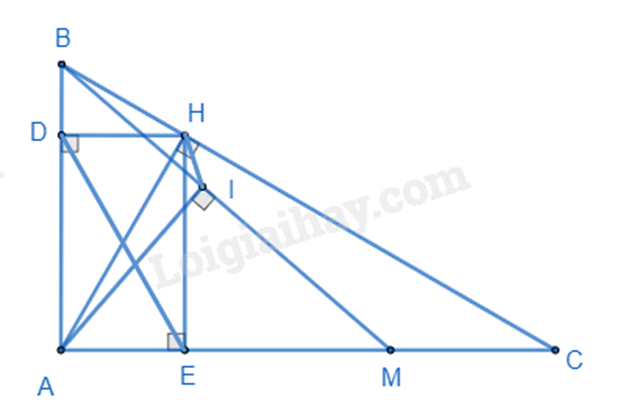
Bộ 10 đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án năm 2024 (ảnh 3)

a) Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore trong tam giác, ta có:

$B C^{2} = A B^{2} + A C^{2} = {(2 \sqrt{3})}^{2} + 6^{2} = 48$ suy ra $B C = \sqrt{48} = 4 \sqrt{3} (c m)$

Ta có: $\sin B = \frac{A C}{B C} = \frac{6}{4 \sqrt{3}} = \frac{\sqrt{3}}{2}$ suy ra $\hat{B} = 60^{\circ}$ .

$\hat{C} = 90^{\circ} - \hat{B} = 90^{\circ} - 60^{\circ} = 30^{\circ}$ .

Vậy $B C = 4 \sqrt{3} c m; \hat{B} = 60^{\circ}; \hat{C} = 30^{\circ}$ .

b) Xét tam giác BHD và tam giác HAD có:

$\hat{B D H} = \hat{H D A} (= 90^{\circ})$

$\hat{B H D} = \hat{H A D}$ (cùng phụ với $\hat{D B H}$ )

suy ra $Δ B H D ∽ Δ H A D (g . g)$ nên $\frac{B D}{D H} = \frac{D H}{D A}$ . Do đó $B D . D A = D H^{2}$ . (1)

Xét tam giác CHE và tam giác HAE có:

$\hat{C E H} = \hat{H E A} (= 90^{\circ})$

$\hat{C}$ chung

suy ra $Δ C H E ∽ Δ H A E (g . g)$ nên $\frac{C E}{H E} = \frac{H E}{A E}$ . Do đó $C E . A E = H E^{2}$ . (2)

Từ (1) và (2) suy ra $B D . D A + C E . A E = D H^{2} + H E^{2}$ (3).

Vì tứ giác ADHE có $\hat{D A E} = \hat{A D H} = \hat{A E H} = 90^{\circ}$ nên tứ giác ADHE là hình chữ nhật. Do đó $A H = D E$ .

Áp dụng định lí Pythagore vào tam giác DHE vuông tại H, ta có: $D H^{2} + H E^{2} = D E^{2}$ . Suy ra $D H^{2} + H E^{2} = A H^{2}$ (4)

Từ (3) và (4) suy ra $B D . D A + C E . A E = A H^{2}$ (đpcm)

c) Xét tam giác BIA và tam giác BAM có:

$\hat{B I A} = \hat{B A M} (= 90^{\circ})$

$\hat{B}$ chung

suy ra $Δ B I A ∽ Δ B A M (g . g)$ nên $\frac{B I}{A B} = \frac{A B}{B M}$ . Do đó $B I . B M = A B^{2}$ .

Xét tam giác BHA và tam giác BAC có:

$\hat{B H A} = \hat{B A C} (= 90^{\circ})$

$\hat{B}$ chung

suy ra $Δ B H A ∽ Δ B A C (g . g)$ nên $\frac{B H}{A B} = \frac{A B}{B C}$ . Do đó $B H . B C = A B^{2}$ .

Từ đó ta có $B I . B M = B H . B C$ suy ra $\frac{B I}{B C} = \frac{B H}{B M}$ .

Xét tam giác BHI và tam giác BMC có:

$\hat{B}$ chung

$\frac{B I}{B C} = \frac{B H}{B M}$ (cmt)

nên $Δ B H I ∽ Δ B M C$ suy ra $\frac{H I}{M C} = \frac{B I}{B C}$ .

Xét tam giác AMB vuông tại A, ta có: $\sin \hat{A M B} = \frac{A B}{B M}$ .

Xét tam giác ABC vuông tại A, ta có: $\sin \hat{A C B} = \frac{A B}{B C}$ .

Suy ra $\sin \hat{A M B} . \sin \hat{A C B} = \frac{A B}{B M} . \frac{A B}{B C} = \frac{A B^{2}}{B M . B C} = \frac{B I . B M}{B M . B C} = \frac{B I}{B C} = \frac{H I}{C M}$ .

Vậy $\sin \hat{A M B} . \sin \hat{A C B} = \frac{H I}{C M}$ (đpcm).

Câu 5:

* Chứng minh bất đẳng thức $a b \leq \frac{{(a + b)}^{2}}{4}$ hay ${(a + b)}^{2} - 4 a b \geq 0$

Ta có: ${(a + b)}^{2} - 4 a b \geq 0$ với mọi a, b.

Vậy $a b \leq \frac{{(a + b)}^{2}}{4}$ .

* Áp dụng bất đẳng thức trên để giải.

Gọi hai cạnh của miếng đất lần lượt là x, y (m). ( $0 < x, y < 800$ )

Vì chu vi của mảnh đất là 800m nên ta có: $2 (x + y) = 800$ hay $x + y = 800$ .

Diện tích đất canh tác là $x y$ .

Ta có: $x y \leq \frac{{(x + y)}^{2}}{4} \leq \frac{400^{2}}{4} = 40000 (m^{2})$ .

Dấu “=” xảy ra là giá trị lớn nhất của xy. Khi đó kích thước của mảnh đất thỏa mãn $x + y = 400$ và $x y = 40000$ .

Ta có $x + y = 400$ nên $y = 400 - x$ .

Thay vào $x y = 40000$ , ta được:

$\begin{array}{l} (400 - x) x = 40000 \\ - x^{2} + 400 x - 40000 = 0 \\ x^{2} - 400 x + 40000 = 0 \\ {(x - 200)}^{2} = 0 \\ x = 200 \end{array}$

Khi đó $y = 400 - 200 = 200$ .

Vậy người đó phải chọn mảnh đất có kích thước 200m x 200m để diện tích đất canh tác là lớn nhất.

Đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Chân trời sáng tạo

Năm học 2024 - 2025

Môn: Toán lớp 9

Thời gian làm bài: phút

(Đề số 2)

A. TRẮC NGHIỆM (4,0 điểm)

Phần 1. Câu trắc nghiệm đúng sai

Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 1. Cho phương trình 2x - 5y = 1 (*)

	Đúng	Sai
a) Cặp số (-2;1) là nghiệm của phương trình (*).
b) Phương trình (*) là phương trình bậc nhất hai ẩn có vô số nghiệm.
c) Hệ số a; b; c của phương trình (*) lần lượt là 2; 5; 1.
d) Tập hợp các điểm có tọa độ (x;y) thỏa mãn phương trình (*) là một đường thẳng

Phần 2. Câu trắc nghiệm nhiều phương án lựa chọn

Trong mỗi câu hỏi từ câu 2 đến câu 7, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 2. Điều kiện xác định của phương trình $\frac{1}{x - 2} + \frac{x}{x + 1} = - \frac{1}{2}$ là

A. x ≠ 2.

B. x ≠ -1.

C. x ≠ 2 và x ≠ -1.

D. x ≠ 2 và x ≠ 0.

Câu 3. Cặp số nào sau đây là nghiệm của hệ phương trình $\{\begin{cases} 2 x + 3 y = 3 \\ - 4 x - 5 y = 9 \end{cases}$ ?

A. (1;1).

B. (-21;15).

C. (1;-1).

D. (21;-15).

Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

A. x + y > 8.

B. 0x + 5 ≥ 0.

C. 2x - 3 > 4.

D. x² - 6x + 1 ≤ 0.

Câu 5. Biển báo giao thông trong hình bên báo đường cấm các xe cơ giới và thô sơ (kể cả các xe được ưu tiên theo quy định) có độ dài toàn bộ kể cả xe và hàng lớn hơn trị số ghi trên biển đi qua. Nếu xe có chiều rộng lớn hơn 3,2m thì không được phép lưu thông để đảm bảo an toàn cho cả xe và các phương tiện khác, cũng như tránh gây cản trở giao thông. Nếu một xe tải đi trên đường đó có chiều rộng a (m) thỏa mãn điều kiện gì?

10 Đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo (có đáp án + ma trận)

A. a = 3,2.

B. a > 3,2.

C. a > 3,2.

D. a ≤ 3,2.

Câu 6. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90° và α = 0,5. Khẳng định nào sau đây là đúng?

A. cos β = 0,5.

B. sin β = 0,5.

C. tan β = 0,5.

D. cot β = 0,5.

Câu 7. Cho tam giác ABC vuông tại A. Hệ thức nào sau đây là sai?

A. BC = $\frac{A C}{\sin B}$ .

B. BC = $\frac{A B}{\sin C}$ .

C. BC = $\frac{A C}{\cos C}$ .

D. BC = $\frac{A C}{\tan C}$ .

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn

Trong mỗi câu 8 và câu 10, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 8. Nghiệm lớn nhất của phương trình (4 - 2x)(x + 1) là bao nhiêu?

Câu 9. Số nguyên nhỏ nhất thỏa mãn bất phương trình x(5x + 1) + 4(x + 3) ≥ 5x² là bao nhiêu?

Câu 10. Biết 0° < α < 90° tính giá trị biểu thức A = $\frac{\sin α + 3 \cos (90 ° - α)}{\sin α - 2 \cos (90 ° - α)}$ .

B. TỰ LUẬN (6,0 điểm)

Bài 1. (2,0 điểm) Giải các phương trình và bất phương trình sau:

a) $\frac{x - 1}{x + 2} - \frac{x}{x - 2} = \frac{4 - 6 x}{x^{2} - 4}$ ;

b) $\frac{4 x - 1}{2} + \frac{6 x - 19}{6} \geq \frac{9 x - 11}{3}$ .

Bài 2. (2,5 điểm)

1. Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại 180 ml nặng trung bình 10kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5,25 tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng 65 kg?

2. Giải bài toán sau bằng cách lập hệ phương trình:

Do ảnh hưởng của dịch Covid – 19 nên trong tháng hai cả hai tổ công nhân chỉ làm được 700 sản phẩm. Sang tháng ba, tình hình dịch ổn định tổ I vượt mức 20% tổ II vượt mức 15% nên cả hai tổ làm được 830 sản phẩm. Hỏi trong tháng hai mỗi tổ làm được bao nhiêu sản phẩm?

Bài 3. (2,0 điểm) Lúc 6 giờ sáng, bạn An đi từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc đỉnh C được mô tả như hình vẽ dưới. Cho biết đoạn AB dài 762 m, $\hat{A} = 4 °, \hat{B} = 6 °$ .

10 Đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo (có đáp án + ma trận)

a) Tính chiều cao con dốc (làm tròn kết quả đến hàng đơn vị của mét).

b) Hỏi bạn An đến trường lúc mấy giờ (làm tròn kết quả đến phút)? Biết rằng tốc độ lên dốc là 4 km/h và tốc độ xuống dốc là 19 km/h.

Bài 4. (0,5 điểm) Cho x, y là hai số thực thỏa mãn điều kiện x² + 2y² + 2xy + 7x + 7y + 10 = 0.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = $\frac{2 x + 2 y - 3}{x + y + 6}$ .

-----HẾT-----

ĐÁP ÁN

A. TRẮC NGHIỆM (4,0 điểm)

Bảng đáp án trắc nghiệm:

Câu

Đáp án

x = 2

-1

B. TỰ LUẬN (6,0 điểm)

Bài 1. (2,0 điểm)

10 Đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo (có đáp án + ma trận)

Bài 2. (2,5 điểm)

1. Đổi 5,25 tấn 5 250 kg

Gọi x (thùng) là số sữa mà xe có thể chở x ∈ ℕ*.

Khi đó, khối lượng sữa mà xe chở là: 10x (kg).

Tổng khối lượng sữa và bác tài xế là: 65 + 10x (kg).

Do trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5 250 kg nên ta có

65 + 10x ≤ 5 250

10x ≤ 5 185

x ≤ 518,5

Mà x ∈ ℕ* nên xe tải đó có thể chở tối đa 518 thùng sữa.

2. Gọi x, y lần lượt là số sản phẩm mà tổ I và tổ II làm được trong tháng 2 (0 < x, y < 700).

Tháng 2 hai tổ làm được 700 sản phẩm nên ta có: x + y = 700 (sản phẩm) (1)

Số sản phẩm tổ I làm được trong tháng 3 là: x + 20%.x = 1,2x (sản phẩm).

Số sản phẩm tổ II làm được trong tháng 3 là: y + 15%.y = 1,15y (sản phẩm).

Tháng 3 hai tổ làm được 830 sản phẩm nên ta có: 1,2x + 1,15y = 830 (sản phẩm) (2)

Từ (1) và (2) ta có hệ phương trình $\{\begin{cases} x + y = 700 \\ 1,2 x + 1,15 y = 830 \end{cases}$ .

Từ phương trình thứ nhất ta có x + y = 700 suy ra x = 700 - y. Thế vào phương trình thứ hai, ta được:

1,2(700 - y) + 1,15y = 830, suy ra 0,05y = 10 hay y = 200 (thỏa mãn).

Từ đó x = 700 - y = 700 - 200 = 500 (thỏa mãn).

Vậy trong tháng 2 tổ I làm được 500 sản phẩm, tổ II làm được 200 sản phẩm.

Bài 3. (2,0 điểm)

a) Kẻ CH ⊥ AB, H ∈ AB. Khi đó CH là chiều cao của con dốc.

10 Đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo (có đáp án + ma trận)

Bài 4. (0,5 điểm)

Ta có: x² + 2y² + 2xy + 7x + 7y + 10 = 0

(x² + 2xy + y²) + 7x + 7y + y² + 10 = 0

(x + y)² + 7(x + y) + y² + 10 = 0 (1)

Đặt S = x + y.

10 Đề thi Giữa kì 1 Toán 9 Chân trời sáng tạo (có đáp án + ma trận)

Vậy giá trị nhỏ nhất của biểu thức P là -13 khi x = -5; y = 0.

Và giá trị lớn nhất của biểu thức P là $\frac{- 7}{4}$ khi x = -2; y = 0.

-----HẾT-----

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

337

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

272

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

218

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

228

Tìm kiếm