Tailieumoi.vn xin giới thiệu Đề cương ôn tập học kì 1 Toán 12 Kết nối tri thức năm 2024 – 2025. Tài liệu được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em làm quen với các dạng bài tập, nâng cao kỹ năng làm bài và rút kinh nghiệm cho bài thi học kì 1 Toán 12. Mời các bạn cùng đón xem:

Đề cương ôn tập học kì 1 Toán 12 Kết nối tri thức năm 2024

A. NỘI DUNG ÔN TẬP

Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

1. Tính đơn điệu và cực trị của hàm số

2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số

3. Đường tiệm cận của đồ thị hàm số

4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số

5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Vecto và hệ trục tọa độ trong không gian

1. Vecto trong không gian

2. Hệ trục tọa độ trong không gian

3. Biểu thức tọa độ của các phép toán vecto

Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm

1. Khoảng biến thiên và khoảng tứ phân vị

2. Phương sai và độ lệch chuẩn

B. BÀI TẬP

ĐỀ BÀI

Phần I: Trắc nghiệm nhiều phương án lựa chọn

Câu 1. Cho hàm số y = f(x) có đồ thị như hình vẽ.

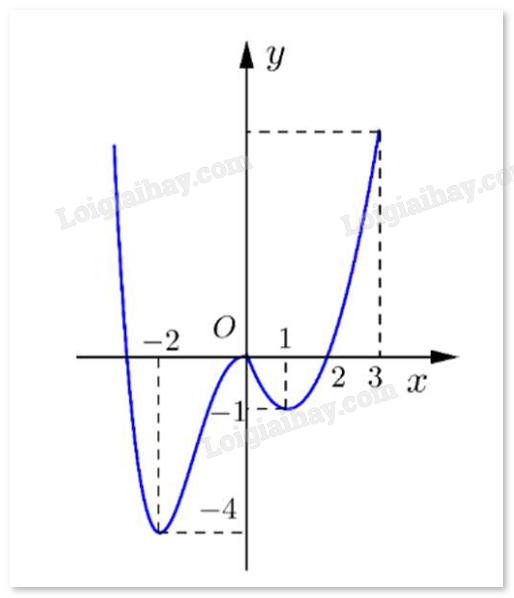
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $(-1;0)$

B. $(-2;-1)$

C. $(0;1)$

D. $(1;3)$

Câu 2. Cho hàm số y = f(x) có bảng biến thiên sau:

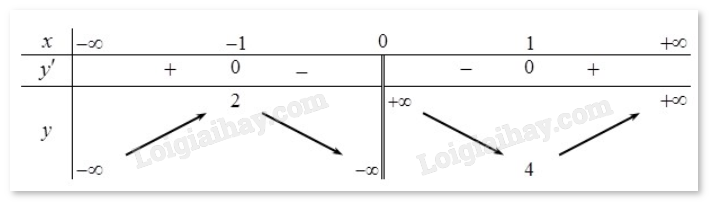
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $(-1;1)$

B. $(4;+\mathrm{\infty })$

C. $(-\mathrm{\infty };2)$

D. $(0;1)$

Câu 3. Cho hàm số f(x) có đạo hàm f’(x) xác định, liên tục trên $\mathbb{R}$ và f’(x) có đồ thị như hình vẽ.

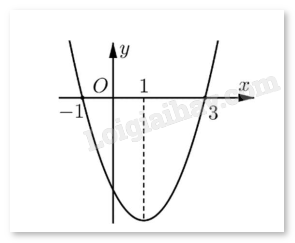
Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên $(1;+\mathrm{\infty })$

B. Hàm số đồng biến trên $(-\mathrm{\infty };-1)$ và $(3;+\mathrm{\infty })$

C. Hàm số nghịch biến trên $(-\mathrm{\infty };1)$

D. Hàm số đồng biến trên $(-1;3)$

Câu 4. Cho hàm số f(x) liên tục trên $\mathbb{R}$ và có đạo hàm $f^{\prime }(x)=(x+1)(3-x{)}^2$. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

A. $(-1;0)$

B. $(-\mathrm{\infty };0)$

C. $(-3;+\mathrm{\infty })$

D. $(-\mathrm{\infty };-1)$

Câu 5. Hàm số nào đồng biến trên tập $\mathbb{R}$ trong các hàm số dưới đây?

A. $y=x^4$

B. $y=x^3+2x$

C. $y=x^2+x+1$

D. $y=-3x+2$

Câu 6. Cho hàm số f(x), bảng xét dấu của f’(x) như sau:

Số diểm cực trị của hàm số đã cho là

A. 0

B. 2

C. 1

D. 3    

Câu 7. Cho hàm số f(x) liên tục trên $\mathbb{R}$ và có bảng xét dấu f’(x) như sau:

Số diểm cực đại của hàm số đã cho là

A. 4

B. 2

C. 3

D. 0

Câu 8. Cho hàm số f(x) có đạo hàm $f^{\prime }(x)=x(x+1{)}^2(x-2{)}^3$, $\mathrm{\forall }x\in \mathbb{R}$. Số điểm cực trị của hàm số là

A. 1

B. 2

C. 3

D. 4

Câu 9. Cho hàm số $y=\sqrt{x^2-4x}$. Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực đại tại x = 4

B. Hàm số không có cực trị

C. Hàm số đạt cực tiểu tại x = 0

D. Hàm số có 2 điểm cực trị

Câu 10. Cho hàm số f(x) liên tục trên [-1;5] và có đồ thị trên đoạn [-1;5] như hình vẽ:

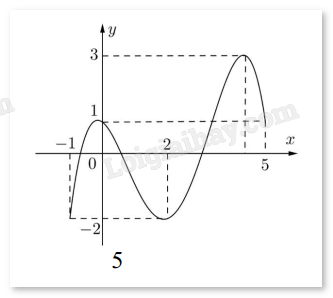
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [-1;5] bằng

A. -1

B. 4

C. 1

D. 2

Câu 11: Cho hàm số y = f(x) xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên

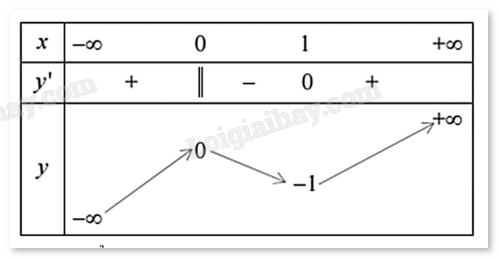
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có giá trị cực tiểu bằng 1

B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1

C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

D. Hàm số có đúng một cực trị

Câu 12. Cho hàm số f(x) có bảng xét dấu đạo hàm như sau:

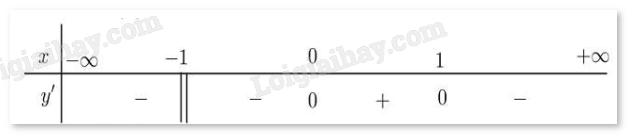
A. $\underset{(-1;1]}{maxf(x)=f(0)}$

B. $\underset{(0;+\mathrm{\infty }]}{maxf(x)=f(1)}$

C. $\underset{(-\mathrm{\infty };-1)}{minf(x)=f(-1)}$

D. $\underset{(-1;+\mathrm{\infty })}{minf(x)=f(0)}$

Câu 13. Giá trị nhỏ nhất của hàm số $f(x)=x^4-10x^2+2$ trên đoạn [-1;2] bằng

A. 2

B. -23

C. -22

D. -7

Câu 14. Giá trị nhỏ nhất của hàm số $f(x)=\frac{x^2+3}{x-1}$ trên đoạn [2;4] bằng

A. $-3$

B. $\frac{19}{3}$

C. $6$

D. $-2$

Câu 15. Giá trị nhỏ nhất của hàm số $f(x)=\frac{\ln x}{x}$ trên đoạn [2;3] bằng

A. $\frac{\ln 2}{2}$

B. $\frac{\ln 3}{3}$

C. $\frac{3}{e^2}$

D. $\frac{1}{e}$

Câu 16. Tiệm cận ngang của đồ thị hàm số $y=\frac{x-2}{x+1}$ là

A. $y=-2$

B. $y=1$

C. $x=-1$

D. $x=2$

Câu 17. Tiệm cận đứng của đồ thị hàm số $y=\frac{x-1}{x-3}$ là

A. $x=-3$

B. $x=-1$

C. $x=1$

D. $x=3$

Câu 18. Đồ thị của hàm số $y=2x+1+\frac{2}{3x-1}$ có đường tiệm cận xiên là

A. $y=3x-1$

B. $y=2+x$

C. $y=3-x$

D. $y=2x+1$

Câu 19. Trong không gian cho 3 điểm M, N, P phân biệt. Tính $\overrightarrow{PM}+\overrightarrow{MN}$.

A. $\overrightarrow{NM}$

B. $\overrightarrow{MN}$

C. $\overrightarrow{NP}$

D. $\overrightarrow{PN}$

Câu 20. Trong không gian cho 3 điểm M, N, P phân biệt. Tính $\overrightarrow{PM}+\overrightarrow{MN}$.

A. $\overrightarrow{NM}$

B. $\overrightarrow{MN}$

C. $\overrightarrow{NP}$

D. $\overrightarrow{PN}$

Câu 21. Cho hình hộp ABCD.A’B’C’D’. Vecto $\overrightarrow{u}=\overrightarrow{A^{\prime }A}+\overrightarrow{A^{\prime }{B}^{\prime }}+\overrightarrow{A^{\prime }{D}^{\prime }}$ bằng vecto nào dưới đây?

A. $\overrightarrow{A^{\prime }C}$

B. $\overrightarrow{C{A}^{\prime }}$

C. $\overrightarrow{A{C}^{\prime }}$

D. $\overrightarrow{C^{\prime }A}$

Câu 22. Gọi I là trung điểm của AB. Khẳng định nào sau đây sai?

A. $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$

B. $IA=IB$

C. $\overrightarrow{IA}=\overrightarrow{IB}$

D. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$

Câu 23. Cho hai vecto $\overrightarrow{u},\overrightarrow{v}$ có $\left|\overrightarrow{u}\right|=3$, $\left|\overrightarrow{v}\right|=4$ và góc giữa hai vecto $\overrightarrow{u},\overrightarrow{v}$ bằng ${60}^o$. Tích vô hướng $\overrightarrow{u},\overrightarrow{v}$ bằng

A. 12

B. 6

C. -12

D. -6

Câu 24. Trong không gian với hệ tọa độ Oxyz, cho vecto $\overrightarrow{u}=-2\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k}$. Tọa độ của vecto $\overrightarrow{u}$ là

A. $(-2;-1;3)$

B. $(2;1;3)$

C. $(-2;0;3)$

D. $(-2;-1;-3)$

Câu 25. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-3;1), B(3;0;-2). Tính độ dài AB.

A. $26$

B. $22$

C. $\sqrt{26}$

D. $\sqrt{22}$

Câu 26. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-4;3) và B(2;2;7). Trung điểm của đoạn thẳng AB có tọa độ là

A. $(4;-2;10)$

B. $(1;3;2)$

C. $(2;6;4)$

D. $(2;-1;5)$

Câu 26. Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh là a. Khi đó, $\overrightarrow{AB}.\overrightarrow{AD}$ bằng

A. $a^2$

B. $0$

C. $a$

D. $\frac{a^2}{2}$

Câu 27. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(-1;2;5) và C(0;0;1). Trọng tâm G của tam giác ABC có tọa độ là

A. $(0;0;3)$

B. $(0;0;9)$

C. $(-1;0;3)$

D. $(0;0;1)$

Câu 28. Kết quả khảo sát cân nặng của một thùng táo ở một lô hàng cho trong bảng sau:

Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là

A. $R=5$

B. $R=24$

C. $R=25$

D. $R=10$

Câu 29. Gọi $Q_1,Q_2,Q_3$ là tứ phân vị của một mẫu số liệu ghép nhóm. Khi đó khoảng tứ phân vị ${\mathrm{\Delta }}_Q$ của mẫu số liệu trên được xác định bởi công thức

A. ${\mathrm{\Delta }}_Q=Q_2-Q_1$

B. ${\mathrm{\Delta }}_Q=Q_3-Q_1$

C. ${\mathrm{\Delta }}_Q=Q_2-Q_3$

D. ${\mathrm{\Delta }}_Q=Q_1-Q_3$

Câu 30. Một ý nghĩa của khoảng tử phân vị là

A. Khoảng tử phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị không bất thường của mẫu số liệu đó

B. Khoảng tử phân vị thường không được sử dụng thay cho khoảng biến thiên

C. Khoảng tử phân vị của mẫu số liệu ghép nhóm xếp xí khoảng tử phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa mẫu số liệu

D. Khoảng tử phân vị của mẫu số liệu ghép nhóm xếp xí khoảng tử phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ không phân tán của nửa mẫu số liệu

Phần II: Trắc nghiệm đúng sai

Câu 31. Cho hàm số $y=f(x)=\frac{x^2+3x}{x-1}$.

a) Hàm số f(x) đồng biến trên khoảng $(-\mathrm{\infty };1)$.

b) Giá trị cực đại của hàm số f(x) là 1.

c) Hàm số f(x) có ba điểm cực trị.

d) Hàm số f(x) nghịch biến trên khoảng (-1;3).

Câu 32. Trong không gian Oxyz, cho $\overrightarrow{a}=(1;2;-3)$, $\overrightarrow{b}=(3;1;5)$.

a) $\overrightarrow{a}+\overrightarrow{b}=(4;3;2)$.

b) $2\overrightarrow{a}-3\overrightarrow{b}=(-7;1;21)$.

c) $\overrightarrow{a}.\overrightarrow{b}=10$.

d) $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=-\frac{\sqrt{10}}{7}$.

Câu 33. Cho hàm số $y=\frac{ax+1}{cx+d}$ có đồ thị như hình vẽ.

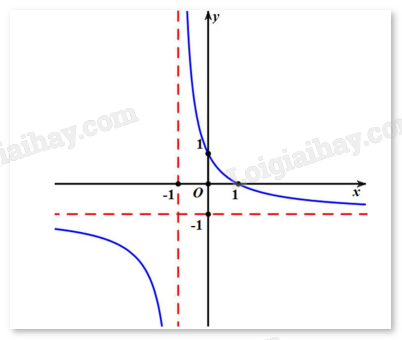
a) Hàm số luôn nghịch biến trên từng khoảng xác định.

b) $\underset{x\to +\mathrm{\infty }}{lim}y=-1$.

c) $\underset{x\to -1^{+}}{lim}y=-\mathrm{\infty }$.

d) Hệ số a = 2.

Câu 34. Bảng sau biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng).

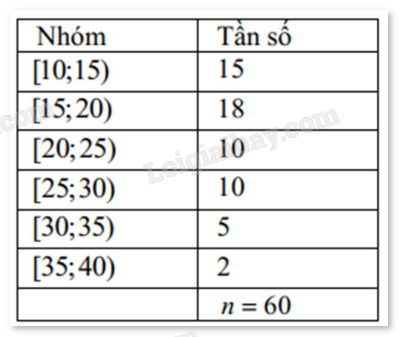
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là R = 30.

b) Số phần tử của mẫu là n = 60.

c) Tứ phân vị thứ nhất là $Q_1=15$.

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là ${\mathrm{\Delta }}_Q=3$.

Phần III: Trắc nghiệm trả lời ngắn

Câu 35. Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được x mét vải lụa $(1\le x\le 18)$. Tổng chi phí sản xuất x mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí: $C(x)=x^3-3x^2-20x+500$. Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với 220 nghìn đồng/mét. Gọi L(x) là lợi nhận thu được khi bán x mét vải lụa. Hỏi lợi nhuân (đơn vị: nghìn đồng) tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày?

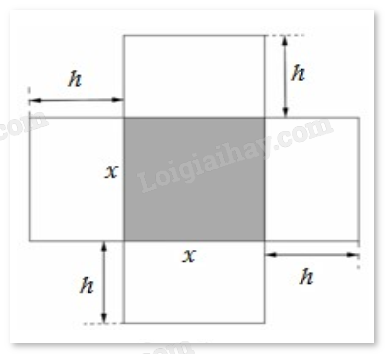
Câu 36. Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao là h (cm) và thể tích là 4000 $c{m}^3$. Tìm độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

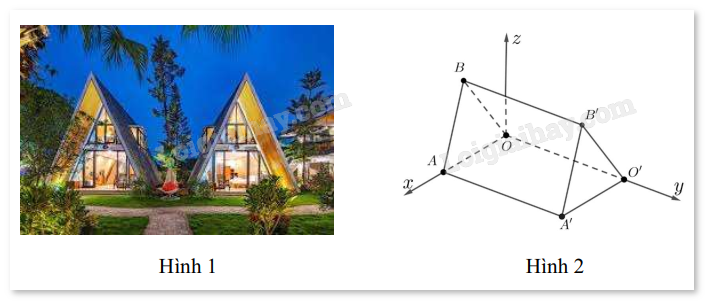
Câu 37. Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác OAB⋅O′A′B′. Với hệ trục toạ độ Oxyz thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm A′ và B′ có tọa độ lần lượt là (240;450;0) và̀ (120;450;300). Mỗi căn nhà gỗ có chiều dài là a cm, chiều rộng là b cm, mỗi cạnh bên củ mặt tiền có độ dài là c cm. Tính a + b + c (làm tròn đến hàng đơn vị).

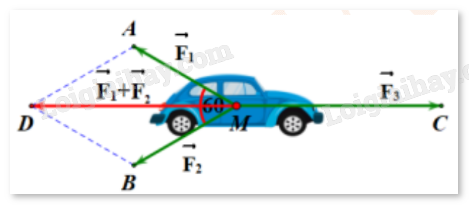
Câu 38. Cho ba lực $\overrightarrow{F_1}=\overrightarrow{MA}$, $\overrightarrow{F_2}=\overrightarrow{MB}$, $\overrightarrow{F_3}=\overrightarrow{MC}$ cùng tác động vào một ô tô tại điểm M và ô tô đứng yên. Cho biết cường độ hai lực $\overrightarrow{F_1}$, $\overrightarrow{F_2}$ đều bằng 25N và $\widehat{AMB}={60}^o$. Khi đó, cường độ lực $\overrightarrow{F_3}$ là (kết quả làm tròn đến hàng phần mười)?

Câu 39. Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:

Tính khoảng tứ phân vị của mẫu số liệu (làm tròn kết quả đến hàng phần mười).

Câu 40. Cho mẫu số liệu ghép nhóm cho bởi bảng sau:

Phương sai của mẫu số liệu ghép nhóm trên là (làm tròn đến hàng phần mười)?

LỜI GIẢI

Phần I: Trắc nghiệm nhiều phương án lựa chọn

Phần II: Trắc nghiệm đúng sai

Câu 31. 

Ta có: $y^{\prime }=\frac{(x^2+3x{)}^{\prime }(x-1)-(x^2+3x)(x-1{)}^{\prime }}{{(x-1)}^2}$

$=\frac{(2x+3)(x-1)-(x^2+3x)}{{(x-1)}^2}=\frac{x^2-2x-3}{{(x-1)}^2}$.

Xét $y^{\prime }=0\iff \frac{x^2-2x-3}{{(x-1)}^2}=0\iff [\begin{array}{l}x=-1\\ x=3\end{array}$.

Bảng biến thiên:

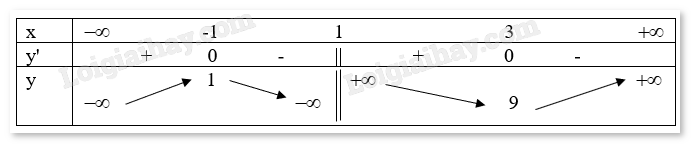
a) Sai. Hàm số đồng biến trên $(-\mathrm{\infty };-1)$ và nghịch biến trên (-1;1).

b) Đúng. Giá trị cực đại của hàm số là y = 1.

c) Sai. Hàm số có hai cực trị là x = -1, x = 3.

d) Sai. Hàm số nghich biến trên (-1;1) và (1;3).

Câu 32. 

a) Đúng. $\overrightarrow{a}+\overrightarrow{b}=(1+3;2+1;-3+5)=(4;3;2)$.

b) Sai. $2\overrightarrow{a}-3\overrightarrow{b}=(2.1-3.3;2.2-3.1;2.(-3)-3.5)=(-7;1;-21)$.

c) Sai. $\overrightarrow{a}.\overrightarrow{b}=1.3+2.1-3.5=-10$.

d) Đúng. $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{-10}{\sqrt{1^2+2^2+{(-3)}^2}.\sqrt{3^2+1^2+5^2}}=-\frac{\sqrt{10}}{7}$.

Câu 33. 

a) Đúng. Đồ thị hàm số đi xuống từ trái sang trên từng khoảng xác định.

b) Đúng. $\underset{x\to +\mathrm{\infty }}{lim}y=-1$.

c) Sai. $\underset{x\to -1^{+}}{lim}y=+\mathrm{\infty }$.

d) Sai. Vì đồ thị đi qua điểm (0;1) nên $1=\frac{a.0+1}{c.0+d}\iff d=1$.

Đồ thị có tiệm cận đứng là đường thẳng x = -1 nên $-\frac{d}{c}=-1\iff -\frac{1}{c}=-1\iff c=1$.

Đồ thị có tiệm cận ngang là đường thẳng y = -1 nên $\frac{a}{c}=-1\iff \frac{a}{1}=-1\iff a=-1$.

Vậy hệ số a = -1.

Câu 34. 

a) Đúng. R = 40 – 10 = 30.

b) Đúng. Số phần tử của mẫu là n = 60.

c) Đúng. Giả sử mức lương của công ty là $x_1,x_2,...,x_{60}$ được sắp xếp theo thứ tự không giảm.

Vì $\frac{n}{4}=15$ nên ta có tứ phân vị thứ nhất là $Q_1=10+\frac{\frac{60}{4}-0}{15}(15-10)=15$.

d) Sai. Vì $\frac{3n}{4}=45$ nên ta có tứ phân vị thứ ba là $Q_3=25+\frac{\frac{3.60}{4}-(15+18+10)}{10}(30-25)=26$.

Vậy ${\mathrm{\Delta }}_Q=26-15=11$.

Phần III: Trắc nghiệm trả lời ngắn

Câu 35. 

Ta có: Lợi nhuận = Doanh thu – Chi phí sản xuất.

Tức là: L(x) = Doanh thu – C(x).

Mỗi ngày hộ bán được x mét vải với 200 nghìn đồng/mét nên doanh thu mỗi ngày của hộ là: 220x (nghìn đồng).

Lợi nhuận khi bán được x mét vải: $L(x)=220x-(x^3-3x^2-20x+500)=-x^3+3x^2+240x-500$.

Ta có: $L^{\prime }(x)=-3x^2+6x+240=0\iff [\begin{array}{l}x=10\\ x=-8\end{array}$.

Vì $1\le x\le 18$ nên chỉ xét giá trị x = 10.

Ta có bảng biến thiên:

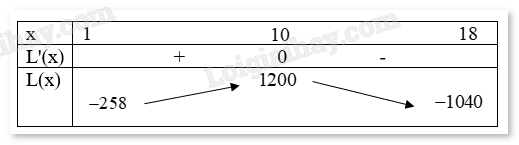
Vậy lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày bằng 1200 nghìn đồng.

Đáp án: 1200.

Câu 36. 

Thể tích của hộp là $V=x^{2}h=4000$ ($c{m}^3$).

Suy ra chiều cao của hộp là $h=\frac{4000}{x^2}$ (cm).

Diện tích xung quanh của hộp là $S(x)=x^2+4xh=x^2+4x\frac{4000}{x^2}=x^2+\frac{16000}{x}$ ($c{m}^2$).

Chiếc hộp làm ra tốn ít bìa nhất khi diện tích xung quanh hình hộp nhỏ nhất.

Ta cần tìm giá trị nhỏ nhất của S(x).

Ta có $S^{\prime }(x)=2x-\frac{16000}{x^2}=0\iff 2x=\frac{16000}{x^2}\iff 2x^3=16000\iff x^3=8000\iff x=20$.

Ta có bảng biến thiên:

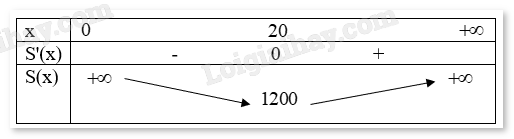
Vậy để tốn ít bìa nhất thì cạnh hình vuông có chiều dài x = 20 (cm).

Đáp án: 20.

Câu 37. 

Ta có: a = AA’, b = A’O’, c = A’B’ = B’O’.

Vì A’ có tọa độ (240;450;0) nên khoảng cách từ A’ đến trục Ox, Oy lần lượt là 450 cm và 250 cm.

Hay AA’ = 450 cm và A’O’ = 240 cm.

Ta có $\overrightarrow{A^{\prime }{B}^{\prime }}=(120-240;450-450;300-0)=(-120;0;300)$.

$A^{\prime }{B}^{\prime }=\left|\overrightarrow{A^{\prime }{B}^{\prime }}\right|=\sqrt{{(-120)}^2+0^2+{300}^2}=60\sqrt{29}$ (cm).

Vì O’O = A’A = 450 cm và O’ nằm trên trục Oy nên O’(0;450;0).

$\overrightarrow{O^{\prime }{B}^{\prime }}=(120-0;450-450;300-0)=(120;0;300)$.

$\left|\overrightarrow{O^{\prime }{B}^{\prime }}\right|=\sqrt{{120}^2+0^2+{300}^2}=60\sqrt{29}$.

Vậy a + b + c = 450 + 240 + $60\sqrt{29}$ $\approx 1013$.

Đáp án: 1013.

Câu 38. 

Ta có $\overrightarrow{F_{12}}=\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MD}$ (với D là điểm sao cho AMBD là hình bình hành).

Có $MA=\left|\overrightarrow{MA}\right|=\left|\overrightarrow{F_1}\right|=25$N, $MB=\left|\overrightarrow{MB}\right|=\left|\overrightarrow{F_2}\right|=25$N.

Mà $\widehat{AMB}={60}^o$ nên $F_{12}=\sqrt{{F_1}^2+{F_2}^2+2F_1{F}_2\cos {60}^o}=\sqrt{{25}^2+{25}^2+\mathrm{2.25.25.}\cos {60}^o}=25\sqrt{3}$N.

Do ô tô đứng yên nên $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}\iff \overrightarrow{F_3}=-\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right)$.

Suy ra $\left|\overrightarrow{F_3}\right|=\left|-\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right)\right|=\left|-\overrightarrow{F_{12}}\right|=25\sqrt{3}$N.

Vậy cường độ của $\overrightarrow{F_3}=25\sqrt{3}\approx 43,3$N.

Đáp án: 43,3.

Câu 39. 

Cỡ mẫu: n = 5 + 12 + 23 + 31 + 29 = 100.

Giả sử tuổi thọ của ong là $x_1,x_2,...,x_{100}$ được sắp xếp theo thứ tự không giảm.

Vì $\frac{n}{4}=25$ nên ta có tứ phân vị thứ nhất là $Q_1=40+\frac{\frac{100}{4}-(5+12)}{23}(60-40)=\frac{1080}{23}$.

Vì $\frac{3n}{4}=75$ nên ta có tứ phân vị thứ ba là $Q_1=80+\frac{\frac{3.100}{4}-(5+12+23+31)}{29}(100-80)=\frac{2400}{29}$.

Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=Q_3-Q_1=\frac{2400}{29}-\frac{1080}{23}\approx 35,8$.

Đáp án: 35,8.

Câu 40. 

Cỡ mẫu: n = 8 + 10 + 11 + 8 + 3 = 40.

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{8.2,5+10.7,5+11.12,5+8.17,5+3.22,5}{40}=11$.

Phương sai của mẫu số liệu ghép nhóm là:

$S^2=\frac{1}{40}\left[8.{(2,5-11)}^2+10.{(7.5-11)}^2+11.{(12,5-11)}^2+8.{(17,5-11)}^2+3.{(22,5-11)}^2\right]=\frac{73}{2}\approx 36,5$.

Đáp án: 36,5.

C. ĐỀ THI MINH HỌA

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Cho hàm số y = f(x) có bảng biến thiên như sau

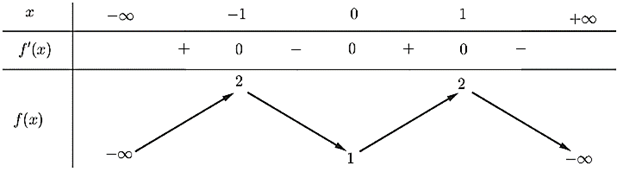
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. (1; +∞).

B. (-1; 0).

C. (-1; 1).

D. (0; 1).

Câu 2. Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là

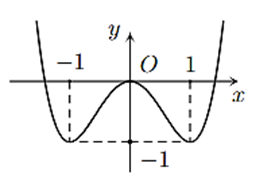
A. $\underset{D}{\min }y=-1$.

B. $\underset{D}{\min }y=1$.

C. $\underset{D}{\min }y=0$.

D. $\underset{D}{\min }y=-2$.

Câu 3. Cho hàm số y = f(x) = $\frac{ax+b}{cx+d}$ có bảng biến thiên như sau:

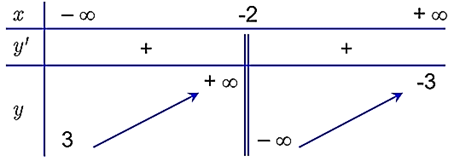
Đồ thị hàm số có bao nhiêu đường tiệm cận

A. 2.

B. 3.

C. 4.

D. 1.

Câu 4. Đồ thị như hình vẽ là của hàm số

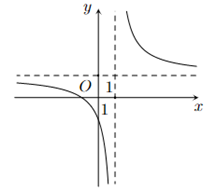
A. $y=\frac{x-1}{-x-1}$.

B. $y=\frac{x+1}{x-1}$.

C. $y=\frac{x+1}{-x+1}$.

D. $y=\frac{x-1}{x+1}$.

Câu 5. Hàm số y = x⁴ - 2x² + 1 nghịch biến trên các khoảng nào sau đây?

A. (-∞; -1) và (0; 1).

B. (-∞; -1) và (0; ∞).

C. (-∞; 0) và (1; +∞).

D. (-1; 0) và (1; +∞).

Câu 6. Hàm số nào sau đây có một đường tiệm cận?

A. $y=\frac{x+3}{2x-1}$.

B. $y=\frac{x^2+3x-2}{x+3}$.

C. $y=\frac{2x}{x^2+1}$.

D. $y=\frac{4}{x-1}$.

Câu 7. Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khi đó, vectơ bằng vectơ $\overrightarrow{AB}$ là vectơ nào dưới đây?

A. $\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$.

B. $\overrightarrow{BA}$.

C. $\overrightarrow{CD}$.

D. $\overrightarrow{B^{\text{'}}{A}^{\text{'}}}$.

Câu 8. Trong không gian Oxyz, cho điểm M (1;-2;3). Chọn khẳng định đúng trong các khẳng định sau.

A. $\overrightarrow{OM}=\overrightarrow{i}-2\overrightarrow{j}+3\overrightarrow{k}$.

B. $\overrightarrow{MO}=\overrightarrow{i}-2\overrightarrow{j}+3\overrightarrow{k}$.

C. $\overrightarrow{OM}=\overrightarrow{k}-2\overrightarrow{j}+3\overrightarrow{i}$.

D. $\overrightarrow{OM}=\overrightarrow{j}-2\overrightarrow{i}+3\overrightarrow{k}$.

Câu 9. Gọi G là trọng tâm của tứ diện ABCD. Trong các khẳng định sau, khẳng định nào sai?

A. $\overrightarrow{AG}=\frac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)$.

B. $\overrightarrow{AG}=\frac{2}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)$.

C. $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$.

D. $\overrightarrow{OG}=\frac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)$.

Câu 10. Trong không gian Oxyz, cho hai vectơ $\overrightarrow{u}=\left(1;0;-1\right)$ và $\overrightarrow{v}=\left(2;1;-2\right)$. Tích vô hướng $\overrightarrow{u}.\overrightarrow{v}$ bằng

A. 0.

B. 1.

C. 4.

D. 2.

Câu 11. Cho mẫu số liệu ghép nhóm cho bởi bảng như hình sau

Khoảng biến thiên của mẫu số liệu là

A. 3.

B. 9.

C. 8.

D. 15.

Câu 12. Cho mẫu số liệu ghép nhóm sau

Gọi $\overline{x}$ là số trung bình cộng của mẫu số liệu trên.

$s^2=\frac{n_1{\left(x_1-\overline{x}\right)}^2+n_2{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+n_m{\left(x_m-\overline{x}\right)}^2}{n}$.

Công thức trên dùng để tính

A. Phương sai.

B. Độ lệch chuẩn.

C. Giá trị trung bình.

D. Độ phân tán.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số y = f(x) xác định trên ℝ và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các khẳng định sau

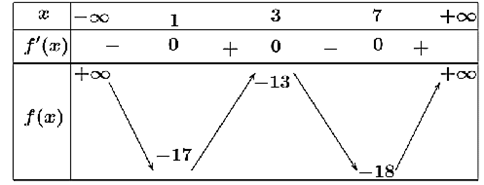
a) Hàm số nghịch biến trên khoảng (1;7).

b) Hàm số đạt giá trị nhỏ nhất tại x = 7.

c) f(1) < f(3).

s

d) Tổng giá trị lớn nhất và giá trị nhỏ nhất là −31.

Câu 2. Cho hàm số y = x³ - 3x + 1. Xét tính đúng hoặc sai của các mệnh đề sau:

a) Hàm số đồng biến trên khoảng (-1;1).

b) Trên khoảng (-∞;1), hàm số có giá trị nhỏ nhất.

c) Hàm số có đồ thị như hình

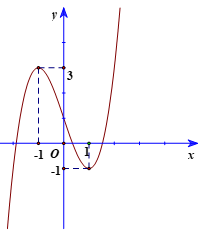
d) Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số. Khi đó, diện tích tam giác ABC là 12 với C(-1;2).

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hình bình hành ABCD có A (-3;4;2), B(-5;6;2), C(-10;17;-7).

a) Tọa độ trung điểm của AB là (-4;5;2).

b) Tọa độ vectơ $\overrightarrow{AB}=\left(2;-2;0\right)$.

c) $\overrightarrow{AB}.\overrightarrow{AD}=10$.

d) Tọa độ chân đường cao vẽ từ A của tam giác ABC là $H\left(-\frac{86}{19};\frac{87}{19};\frac{65}{19}\right)$.

Câu 4. Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B được cho dưới bảng sau.

Xét tính đúng, sai của các mệnh đề sau

a) Khoảng biến thiên của mẫu số liệu nhà đầu tư vào lĩnh vực A là 25.

b) Độ lệch chuẩn của mẫu số liệu số nhà đầu tư vào lĩnh vực A là 5,83 (làm tròn đến hàng phần trăm).

c) Độ lệch chuẩn của mẫu số liệu số nhà đầu tư vào lĩnh vực B là 7,01 (làm tròn đến hàng phần trăm).

d) Nếu so sánh theo độ lệch chuẩn thì tiền lãi của các nhà đầu tư trong lĩnh vực A có xu hướng phân tán rộng hơn so với tiền lãi của các nhà đầu tư trong lĩnh vực B.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.

Câu 1. Một vật chuyển động theo quy luật $s=-\frac{1}{3}{t}^3+6t^2$ với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu m/s?

Câu 2. Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Xác định số tiệm cận của đồ thị hàm số $y=\frac{x^2-1}{f^2\left(x\right)-f\left(x\right)}$.

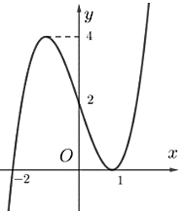
Câu 3. Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200 m³. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 350 nghìn đồng/m². Hãy xác định chi phí thấp nhất để xây bể (làm tròn đến đơn vị triệu đồng).

Câu 4. Giả sử doanh số bán hàng (đơn vị triệu đồng) của một sản phẩm mới trong vòng 1 số năm nhất định tuân theo quy luật logistic được mô hình hóa bằng hàm số f(t) = 500(t² + me^-t), với t ≥ 0 là thời gian tính bằng năm kể từ khi phát hành sản phẩm mới, m ≤ 0 là tham số. Khi đó đạo hàm f'(t) sẽ biểu thị tốc độ bán hàng. Biết rằng tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm, khi đó giá trị nhỏ nhất của m bằng bao nhiêu?

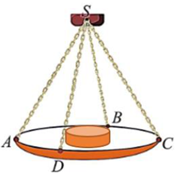
Câu 5. Một chiếc cân đòn tay đang cân một vật có khối lượng m = 3kg được thiết kế với đĩa cân được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp đều có $\widehat{ASC}=90°$. Biết độ lớn của lực căng cho mỗi sợi xích có dạng $\frac{a\sqrt{2}}{4}$. Lấy g = 10m/s². Khi đó giá trị của a bằng bao nhiêu?

Câu 6. Trong không gian Oxyz cho ba điểm A(3;2;-1), B(-1;-x;1), C(7;-1;y). Khi A, B, C thẳng hàng thì giá trị biểu thức x + y bằng bao nhiêu?

BẢNG ĐÁP ÁN

PHẦN I.

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Chọn	D	A	B	B	A	C	A	A	B	C	D	A

PHẦN II.

PHẦN III.