Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Tính chất cơ bản của phân thức đại số được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Tính chất cơ bản của phân thức đại số. Mời các bạn đón xem:
Bài tập Toán 8 Tính chất cơ bản của phân thức đại số
A. Bài tập Tính chất cơ bản của phân thức đại số
Bài 1: Chọn câu sai. Với đa thức ta có:
Đáp án : D
Theo tính chất cơ bản của phân thức đại số, ta có:
(với khác đa thức 0)
(với là một nhân tử chung, khác đa thức 0)
Mệnh đề sai. Ví dụ:
Bài 2: Cho . Khi đó:
Hướng dẫn giải:
Đáp án : D
Bài 3: Mẫu thức chung của các phân thức là?
A.
Hướng dẫn giải:
Đáp án : D
Mẫu thức của hai phân thức là và nên mẫu thức chung có phần hệ số là 2, phần biến số là .
Mẫu thức chung là
Bài 4: Cho . Khi đó:
Hướng dẫn giải:
Đáp án : D
Bài 5: Có bao nhiêu giá trị nguyên của để phân thức có giá trị là một số nguyên?
Đáp án : C
Điều kiện:
Để
Với (loại vì )
Với (thỏa mãn )
Với (loại vì )
Với (thỏa mãn )
Vậy có hai giá trị x để phân thức có giá trị là một số nguyên.
B. Lý thuyết Tính chất cơ bản của phân thức đại số
1. Tính chất cơ bản của phân thức
- Tính chất cơ bản của phân thức:
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
(M là một đa thức khác đa thức không).
Nếu chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
(N là nhân tử chung).
- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
; .
Ví dụ: Để biến đổi phân thức thành , ta chia cả tử và mẫu của phân thức cho y – x, khi đó
2. Rút gọn phân thức
Rút gọn một phân thức là biến đổi phân thức đó thành một phân thức mới bằng nó nhưng đơn giản hơn.
Muốn rút gọn một phân thức đại số ta làm như sau:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung;
- Chia cả tử và mẫu cho nhân tử chung.
3. Quy đồng mẫu thức nhiều phân thức
Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.
Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
- Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC của mẫu thức đó;
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Ví dụ: Quy đồng mẫu thức hai phân thức và
MTC là:
Ta có:
Khi đó:
- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
; .
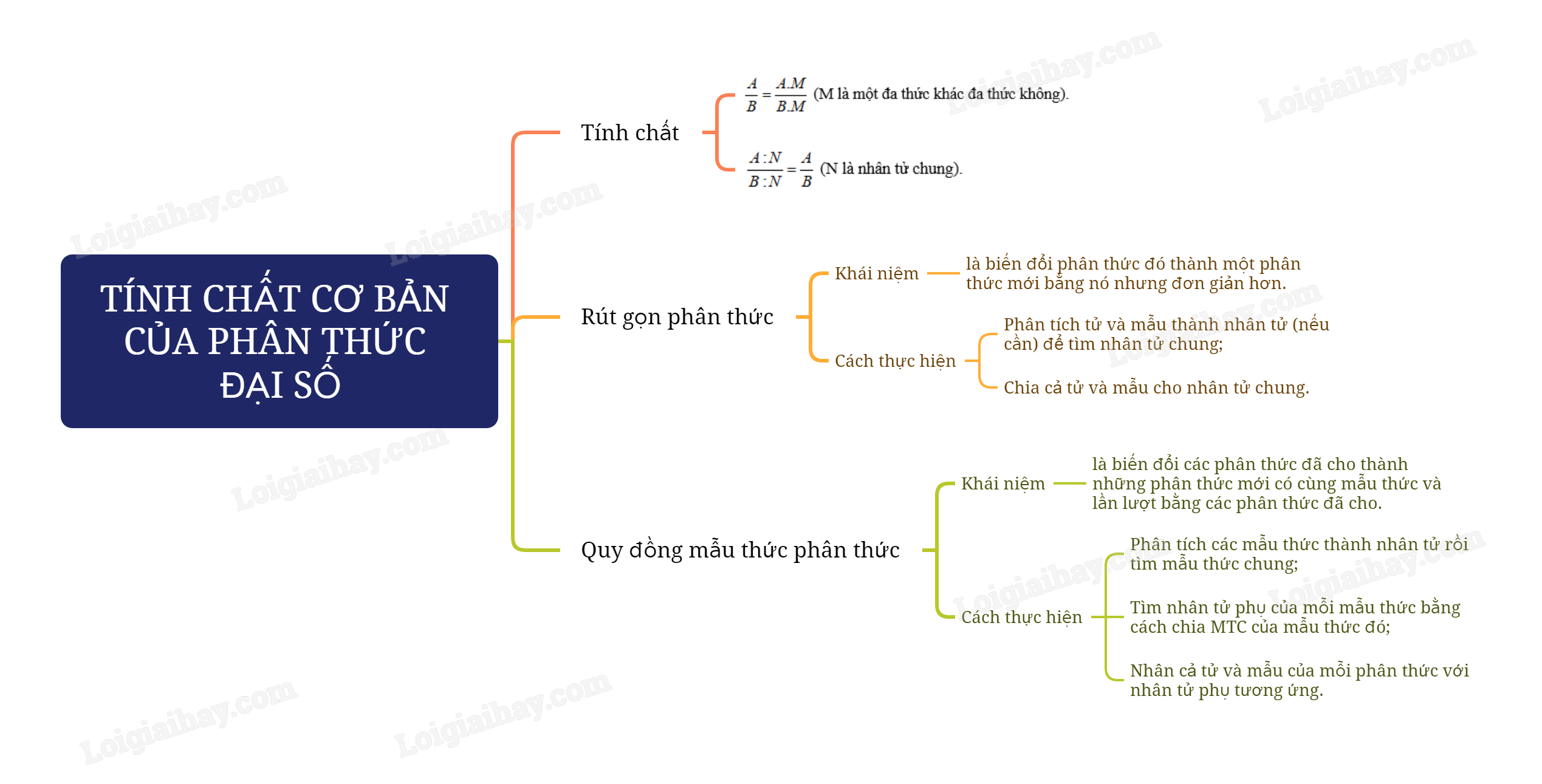
Sơ đồ tư duy Tính chất cơ bản của phân thức đại số