Bài 1. Tính:

a) (‒4,125).(‒2,14)

b) 2,72 . (‒3,25);

c) (‒14,3) : (‒2,5);     

d) 6,24 : (‒0,125)

Hướng dẫn giải

a) (‒4,125).(‒2,14) = 4,125 . 2,14 = 8,8275.

b) 2,72 . (‒3,25) = ‒ (2,72 . 3,25) = ‒ 8,84.

c) (‒14,3) : (‒2,5) = 14,3 : 2,5 = 143 : 25 = 5,72.

d) 6,24 : (‒0,125) = ‒ (6,24 : 0,125) = ‒ (6240 : 125) = ‒ 49,92.

Bài 2. Tính (tính hợp lí nếu có thể):

a) $-\frac{1}{13}.\left(3\frac{1}{4}-6,5\right):\frac{2}{5}+\left(-0,246\right):3$;

b) 5,34 . 26,15 + 5,34 . (‒126,15).

Hướng dẫn giải

a) $-\frac{1}{13}.\left(3\frac{1}{4}-6,5\right):\frac{2}{5}+\left(-0,246\right):3$   

$=-\frac{1}{13}.\left(\frac{13}{4}-\frac{65}{10}\right):\frac{2}{5}+\left[-\left(0,246:3\right)\right]$

$=-\frac{1}{13}.\left(\frac{13}{4}-\frac{13}{5}\right):\frac{2}{5}+\left(-0,082\right)$

$=-\frac{1}{13}\mathrm{.13.}\left(\frac{1}{4}-\frac{1}{5}\right):\frac{2}{5}+\left(-0,082\right)$

$=-\frac{1}{1}\mathrm{.1.}\left(\frac{5}{20}-\frac{4}{20}\right):\frac{2}{5}+\left(-0,082\right)$

$=-\frac{1}{20}.\frac{5}{2}+\left(-0,082\right)$

$=-\frac{1}{4.5}.\frac{5}{2}+\left(-0,082\right)$

$=-\frac{1}{8}+\left(-0,082\right)$

= ‒ 0,125 + (‒0,082)

= ‒ (0,125 + 0,082)

= ‒ 0,207.

b) 5,34 . 26,15 + 5,34 . (‒126,15)

= 5,34 . [26,15 + (‒126,15)]

= 5,34 . [‒ (126,15 – 26,15)]

= 5,34 . (‒100)

= ‒ (5,34 . 100)

= ‒ 534.

Bài 3. Mức tiêu thụ nhiên liệu của một chiếc xe máy Honda SH mode là 1,9 lít trên 100 ki – lô - mét. Giá một lít xăng E5 RON 95 - II ngày 11/04/2022 là 27 309 đồng. Một người đi xe máy đó trên quãng đường 100 km thì sẽ hết bao nhiêu tiền xăng?

Hướng dấn giải

Số tiền xăng người đi xe máy đi hết quãng đường 100 km là:

27 309 . 1,9 = 51 887,1 (đồng)

Vậy để đi được quãng đường 100 km thì người đó hết 51 887,1 đồng tiền xăng.

Bài 4. Một khu đất hình chữ nhật có chiều dài 31,23 m và chiều rộng bằng $\frac{2}{3}$ chiều dài.

a) Người ta lấy $\frac{5}{6}$ diện tích khu đất để đào ao. Tính diện tích ao.

b) Diện tích còn lại người ta trồng rau. Biết cứ 1 m² thì thu hoạch được 2,1 kg rau. Hỏi người ta thu hoạch được bao nhiêu kg rau?

c) Mỗi ki – lô – gam rau người đó bán được 12 000 đồng. Vậy nếu bán hết số rau thu hoạch được thì người đó bán được bao nhiêu tiền?

Hướng dẫn giải

Chiều rộng khu đất hình chữ nhật là: 31,23 .$\frac{2}{3}$  = 20,82 (m)

Diện tích khu đất hình chữ nhật là: 31,23 . 20,82 = 650,2086 (m²)

a) Diện tích người đó dùng để đào ao là: 650,2086 . $\frac{5}{6}$ = 541,8405 (m²).

b) Diện tích còn lại dùng để trồng rau là: 650,2086 – 541,8405 = 108,3681 (m²)

Số kg rau người đó thu hoạch được là: 108,3681 . 2,1 = 227, 57301 (kg).

c) Số tiền người đó bán rau thu được là: 227,57301 . 12 000 = 2 730 876,12 (đồng).

Bài 5. Một căn phòng hình hộp chữ nhật với chiều dài 3,8 m, chiều rộng 3,2 m và chiều cao 3 m. Người ta muốn sơn trần nhà và bốn bức tường bên trong phòng.

a) Tính diện tích cần sơn biết tổng diện tích các cửa là 4,5 m².

b) Biết giá tiền công sơn tường và trần nhà đều là 15 000 đồng. Tính tổng số tiền công sơn căn phòng đó.

Hướng dẫn giải

a) Diện tích trần nhà của căn phòng là: 3,8. 3,2 = 12,16 (m²).

Diện tích bốn bức tường của căn phòng là: 2.(3,8 + 3,2). 3 = 42 (m²)

Diện tích trần nhà và bốn bức tường căn phòng hình hộp chữ nhật là:

12,16 + 42 = 54,16 (m²).

Diện tích cần sơn là: 54,16 – 4,5 = 49,66 (m²).

Vậy diện tích cần sơn là: 49,66 (m²).

b) Số tiền công sơn căn phòng là:

49,66 . 15 000 = 744 900 (đồng).

Vậy số tiền công sơn căn phòng là 744 900 đồng.

Bài 6: Thực hiện phép tính

a) 3, 27. (–2, 2)

b) (–9, 84) : 4, 1

c) (–5,6).(–7, 18)

Lời giải:

a) 3, 27. (–2, 2) = –(3, 27 . 2, 2) = –7, 194

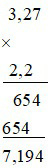
b) (–9, 84) : 4, 1 = –(9, 84 : 4, 1) = –(984 : 410) = –2, 4

c) (–5, 6).(–7, 18) = 5, 6 . 7, 18 = 40, 208

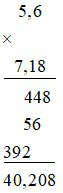
Bài 7: Thực hiện phép tính

a) 4, 6 . 5, 3 + 4, 6 . 4, 7

b) (–1, 2) . (–3,4) + 3, 4 . 8, 8

c) 13, 45 . 3, 6 – 3, 6 . 3, 45

Lời giải:

a) 4, 6 . 5, 3 + 4, 6 . 4, 7

= 4, 6 . (5, 3 + 4, 7) 

= 4, 6 . 10 = 46

b) (–1, 2) . (–3,4) + 3, 4 . 8, 8

= 1, 2 . 3, 4 + 3, 4 . 8, 8

= 3, 4 . (1, 2 + 8, 8)

= 3, 4 . 10 = 34 

c) 13, 45 . 3, 6 – 3, 6 . 3, 45

= 3, 6 . (13, 45 – 3, 45)

= 3, 6 . 10 = 36

Câu 8: Thực hiện các phép tính sau: (−45,5) . 0,4 ta được kết quả là:

A.18,2

B.−18,2

C.−182

D. 1,82

Trả lời:

$\left(-\mathrm{45,5}\right)\mathrm{.0,4}=-\left(\mathrm{45,5.0,4}\right)=-\mathrm{18,2}$

Đáp án cần chọn là: B

Câu 9: Thực hiện các phép tính sau: −0,18 . (−1,5) ta được kết quả là:

A.−0,27

B.−2,7

C.0,27

D.2,7

Trả lời:

 $-\mathrm{0,18.}(-\mathrm{1,5})=\mathrm{0,18.1,5}=\mathrm{0,27}$

Đáp án cần chọn là: C

Câu 10: Thực hiện các phép tính sau: 0,15 . 4,4 ta được kết quả là:

A.6,6

B.0,66

C.6,60

D.0,066

Trả lời:

 $\mathrm{0,15.4,4}=\mathrm{0,66}$

Đáp án cần chọn là: B

Câu 11: Tính diện tích S của một hình tròn có bán kính R = 10cm theo công thức 

S = πR² với π = 3,142

A.31,4cm²

B.314cm²

C.64,8cm²

D.314cm²

Trả lời:

Diện tích hình tròn là: $S={\mathrm{3,14.10}}^2=314c{m}^2$

Đáp án cần chọn là: B

Câu 12:

Điền vào chỗ trống

Diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52 cm là .... cm²

Trả lời:

Diện tích của hình chữ nhật đó là:

 $\mathrm{31,21.22,52}=\mathrm{702,8492}$ (cm²)

Câu 13:

Khối lượng vitamin C trung bình trong một quả ớt chuông là 0,135 g, còn trong một quả cam là 0,045 g. Khối lượng vitamin C trong quả ớt chuông gấp bao nhiêu lần trong quả cam?

A.2 lần

B.3 lần

C.4 lần

D.5 lần

Trả lời:

Khối lượng vitamin C trong quả ớt chuông gấp số lần trong quả cam là:

0,135  :  0,045 = 3 ( lần)

Đáp số: 3 lần.

Đáp án cần chọn là: B

Câu 14: Tính chu vi của một hình tròn có bán kính R = 1,25 m theo công thức

C = 2πR với π = 3,142.

A.7,855 m²

B.7,855 m

C.7,585 m²

D.7,558 m²

Trả lời:

Chu vi của hình tròn đó là:

C = 2πR = 2 . 3,142 . 1,25 = 7,855 (m²)

Đáp số: 7,855 m²

Đáp án cần chọn là: A