Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Dấu hiệu chia hết cho 2, cho 5 được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Dấu hiệu chia hết cho 2, cho 5. Mời các bạn đón xem:
Bài tập Toán 6 Dấu hiệu chia hết cho 2, cho 5
A. Bài tập Dấu hiệu chia hết cho 2, cho 5
Bài 1. Cho các số 82, 980, 5 975, 49 173, 756 598. Trong các số đó:
a) Số nào chia hết cho 5, nhưng không chia hết cho 2?
b) Số nào chia hết cho 2, nhưng không chia hết cho 5?
c) Số nào không chia hết cho 2 và không chia hết cho 5?
Lời giải:
a) Số chia hết cho 5 nhưng không chia hết cho 2 có chữ số tận cùng là 5.
Nên trong các số đã cho, số chia hết cho 5 nhưng không chia hết cho 2 là: 5 975.
b) Số chia hết cho 2 nhưng không chia hết cho 5 có chữ số tận cùng là 2; 4; 6; 8.
Nên trong các số đã cho, các số chia hết cho 2 nhưng không chia hết cho 5 là: 82; 756 598.
c) Số không chia hết cho 2 và không chia hết cho 5 thì không có tận cùng là 0; 2; 4; 5; 6; 8, hay nói cách khác là các số có chữ số tận cùng là 1; 3; 7; 9 thì không chia hết cho cả 2 và 5.
Do đó, trong các số đã cho số không chia hết cho 2 và không chia hết cho 5 là: 49 173.
Bài 2. Cho số N = 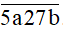 Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 5 dư 1 và N chia hết cho 2.
Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 5 dư 1 và N chia hết cho 2.
Lời giải:
Điều kiện: a, b ∈ {0; 1; 2; 3; ....; 9}
N = 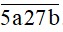 chia cho 5 dư 1 nên b ∈ {1; 6}
chia cho 5 dư 1 nên b ∈ {1; 6}
Mà N chia hết cho 2 nên b = 6, ta được số N = 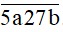
Lại có N là số có 5 chữ số khác nhau nên a ∈ {0; 1; 3; 4; 8; 9}
Vậy có 6 số N thỏa mãn yêu cầu bài là 50 276; 51 276; 53 276; 54 276; 58 276; 59 276.
Bài 3. Từ ba số 2; 3; 7. Hãy ghép thành các số có ba chữ số khác nhau và chia hết cho 2.
Hướng dẫn giải
Số được ghép thành chia hết cho 2 nên phải có chữ số hàng đơn vị là 2.
Hai chữ số hàng chục có thể là 3 hoặc 7.
- Nếu chữ số hàng chục là 3 thì chữ số hàng trăm là 7.
Ta được số cần tìm là 732.
- Nếu chữ số hàng chục là 7 thì chữ số hàng trăm là 3.
Ta được số cần tìm là 372.
Vậy có hai số có thể ghép thành là 372 và 732.
Bài 4. Tìm b để số 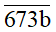
Hướng dẫn giải
Để 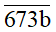
Để 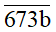
Do đó để 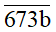
Vậy để 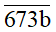
Bài 5. Có bao nhiêu số có hai chữ số chia hết cho 5.
Hướng dẫn giải
Các số có hai chữ số chia hết cho 5 là: 10; 15; 20; ….; 95.
Số các số có hai chữ số chia hết cho 5 là:
(95 – 10) : 5 + 1 = 18 (số)
Vậy có 18 số có hai chữ số chia hết cho 5.
Câu 6. Từ ba trong 4 số 5, 6, 3, 0, hãy ghép thành số có ba chữ số khác nhau là số lớn nhất chia hết cho 2 và 5.
A. 560
B. 360
C. 630
D. 650
Trả lời:
Số chia hết cho 2 và 5 có tận cùng là 0 nên chữ số hàng đơn vị của các số này là 0.
Từ đó ta lập được các số có 3 chữ số khác nhau chia hết cho 2và 5 là:
560; 530; 650; 630; 350; 360.
Số lớn nhất trong 6 số trên là 650.
Vậy số cần tìm là 650.
Đáp án cần chọn là: D
Câu 7. Chọn câu trả lời đúng.
Trong các số 2055; 6430; 5041; 2341; 2305
A. Các số chia hết cho 5 là 2055; 6430; 5041
B. Có hai số chia hết cho 3 là 2055 và 6430
C. Các số chia hết cho 5 là 2055; 6430; 2305
D. Không có số nào chia hết cho 3
Trả lời:
Các số 2055; 6430; 2305 có tận cùng là 0 hoặc 5 nên các số đó chia hết cho 5. Suy ra C đúng, A sai.
Chỉ có mộtsố chia hết cho 3 là 2055 nên B, D sai.
Đáp án cần chọn là: C
Câu 8. Số tự nhiên a chia cho 65 dư 10. Khi đó số tự nhiên a
A. Chia cho 5 dư 1.
B. Chia cho 5 dư 4.
C. Chia cho 5 dư 3.
D. Chia hết cho 5.
Trả lời:
Vì số tự nhiên a chia cho 65 dư 10 nên ta có a = 65q + 10(qϵN)
Mà 65⁝5 và 10⁝5 nên a = 65q + 10chia hết cho 5.
Đáp án cần chọn là: D
Câu 9: Cho các số: 10 250, 768, 35 765, 426. Trong các số đã cho, có bao nhiêu số chia hết cho 5?
A. 1
B. 2
C. 3
D. 4
Lời giải
Theo dấu hiệu chia hết cho 5, các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Trong các số đã cho, ta thấy số 10 250 có chữ số tận cùng là 0, số 35 765 có chữ số tận cùng là 5 nên các số 10 250, 35 765 chia hết cho 5.
Vậy có 2 số chia hết cho 5 trong các số đã cho.
Chọn đáp án B.
Câu 10: Trong các số sau, số nào chia hết cho 2 nhưng không chia hết cho 5:
A. 2 141
B. 1 345
C. 4 620
D. 2 34
Lời giải
Áp dụng dấu hiệu chia hết cho 2, cho 5 để làm bài.
Trong các đáp án, những số chia hết cho 2 là 4 620 và 234.
Vì số đó không chia hết cho 5 nên số cần tìm là 234.
Chọn đáp án D.
Câu 11: Dùng ba chữ số 4; 0; 5 ghép thành các số tự nhiên có ba chữ số khác nhau và chia hết cho 5. Số các chữ số có thể tạo thành là:
A. 2
B. 3
C. 4
D. 5
Lời giải
Số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5.
Những số có chữ số tận cùng là 0 được lập từ ba chữ số 4; 0; 5 là: 450; 540
Những số có chữ số tận cùng là 5 được lập từ ba chữ số 4; 0; 5 là: 405
Vậy có 3 số tự nhiên thỏa mãn đề bài.
Chọn đáp án B.
Câu 12: Tìm số tự nhiên có hai chữ số, các chữ số giống nhau, biết số đó chia hết cho 2 và chia cho 5 thì dư 3.
A. 22
B. 44
C. 66
D. 88
Lời giải
Số chia hết cho 2 có chữ số tận cùng là 0, 2, 4, 6, 8
Số chia cho 5 dư 3 có chữ số tận cùng là 3 hoặc 8
Vậy số chia hết cho 2 và chia cho 5 dư 3 có chữ số tận cùng là 8
Mà số cần tìm có hai chữ số, các chữ số giống nhau nên số đó là 88.
Chọn đáp án D.
Câu 13: Từ ba trong bốn số 5, 6, 3, 0, hãy ghép thành số có ba chữ số khác nhau là số lớn nhất chia hết cho 2 và 5.
A. 560
B. 360
C. 630
D. 650
Lời giải
Số chia hết cho 2 và 5 có chữ số tận cùng là 0 nên chữ số hàng đơn vị là 0
Từ đó ta lập được các số có ba chữ số khác nhau từ các số đã cho thỏa mãn chia hết cho cả 2 và 5 (có chữ số tận cùng là 0) là
560; 530; 650; 630; 350; 360
Trong đó số lớn nhất là: 650
Chọn đáp án D.
Câu 14: Tìm chữ số thích hợp ở dấu * để số 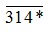 chia hết cho cả 2 và 5.
chia hết cho cả 2 và 5.
A. 0
B. 2
C. 5
D. 9
Lời giải
Ta có * là chữ số hàng đơn vị của số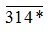 nên * là số tự nhiên nhận giá trị từ 0 đến 9.
nên * là số tự nhiên nhận giá trị từ 0 đến 9.
Lại có 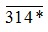 chia hết cho cả 2 và 5 nên chữ số tận cùng của
chia hết cho cả 2 và 5 nên chữ số tận cùng của 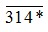 phải là 0
phải là 0
Vậy * = 0.
Chọn đáp án A.
Câu 15: Ở tiết mục nhảy theo cặp của đội cổ vũ, số người của đội được xếp vừa hết. Khi biểu diễn theo nhóm, mỗi nhóm gồm 5 người, đội cổ vũ còn thừa ra 1 người. Đội cổ vũ đó có bao nhiêu người, biết rằng số người của đội khoảng từ 25 đến 30 người.
A. 26
B. 27
C. 28
D. 29
Lời giải
Gọi số người của đội cổ vũ là x (người, 25 ≤ x ≤ 30, x ∈ N).
Vì ở tiết mục nhảy theo cặp (hai người ghép thành 1 cặp), số người của đội được xếp vừa hết nên x chia hết cho 2.
Trong các số từ 25 đến 30, theo dấu hiệu chia hết cho 2, ta thấy chỉ có các số 26, 28, 30 là thỏa mãn.
Lại có khi biểu diễn theo nhóm, mỗi nhóm 5 người, đội cổ vũ còn thừa ra 1 người, nghĩa là x chia cho 5 dư 1.
Mà 26 : 5 = 5 (dư 1), 28 : 5 = 5 (dư 3), 30 : 5 = 6
Do đó x = 26 (t/m).
Vậy đội cổ vũ có 26 người.
Chọn đáp án A.
Câu 16. Cho chia hết cho 2. Số thay thế cho * có thể là
A. 1
B. 2
C. 3
D. 5
Trả lời:
Vì * là chữ số tận cùng của nên * chỉ có thể là 0; 2; 4; 6; 8.
Vậy số 2 là số cần tìm.
Đáp án cần chọn là: B
Câu 17. Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
A. 0, 1, 2, 3
B. 0, 2, 4, 6, 8
C. 1, 3, 5, 7, 9
D. 0 hoặc 5
Trả lời:
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Đáp án cần chọn là: D
Câu 18. Trong những số sau, có bao nhiêu số chia hết cho 2?
100000984, 12345, 12543456, 1234567, 155498
A. 2
B. 3
C. 4
D. 5
Trả lời:
Các số 100000984, 12543456, 155498 có chữ số tận cùng là số chẵn nên chia hết cho 2.
Các số còn lại có chữ số tận cùng là số lẻ (5, 7) nên không chia hết cho 2.
Vậy có 3 số chia hết cho 2.
Đáp án cần chọn là: B
Câu 19. Tổng chia hết cho 5 là
A. A = 5+15+70+1995
B. B = 10+25+34+2000
C. C = 25+15+33+45
D. D = 15+25+1000+2007
Trả lời:
Vì 5⁝5; 15⁝5; 70⁝5; 1995⁝5 nên A = (5+15+70+1995)⁝5
Đáp án cần chọn là: A
Câu 20. Hãy chọn câu sai:
A. Số chia hết cho 2 và 5 có tận cùng là số 0
B. Một số chia hết cho 10 thì số đó chia hết cho 2
C. Số chia hết cho 2 thì có tận cùng là số lẻ
D. Số dư trong phép chia một số cho 2 bằng số dư trong phép chia chữ số tận cùng của nó cho 2
Trả lời:
Số chia hết cho 2 có tận cùng là số chẵn nên câu sai là: Số chia hết cho 2 có tận cùng là số lẻ.
Đáp án cần chọn là: C
B. Lý thuyết Dấu hiệu chia hết cho 2, cho 5
1. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Ví dụ:
a) Số 15 552 chia hết cho 2 vì có chữ số tận cùng là 2.
b) Số 955 không chia hết cho 2 vì có chữ số tận cùng là 5 (5 không là số chẵn).
2. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ: Xét số 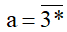
Hướng dẫn giải
Chữ số tận cùng của a là ∗ nên để a chia hết cho 5 thì ∗ phải là 0 hoặc 5.
Để a không chia hết cho 5 thì ∗ phải khác 0 hoặc 5, tức là các số 1; 2; 3; 4; 6; 7; 8; 9.
Vậy thay ∗ bằng 1; 2; 3; 4; 6; 7; 8; 9 thì a không chia hết cho 5.