Với giải sách bài tập Toán 6 Bài 7: Dấu hiệu chia hết cho 2 và cho 5 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 7: Dấu hiệu chia hết cho 2 và cho 5

Bài 1 trang 21 sách bài tập Toán lớp 6 Tập 1: Trong những số từ 2 000 đến 2 009, số nào

a) chia hết cho 2?

b) chia hết cho 5?

c) chia hết cho 10?

Lời giải:

Các số từ 2 000 đến 2 009 là: 2 000; 2 001; 2 002; 2 003; 2 004; 2 005; 2 006; 2 007; 2 008; 2 009.

Ta có 2 000 có chữ số tận cùng là 0 nên 2 000 chia hết cho 2 và cho 5;

2 001 có chữ số tận cùng là 1 nên 2 001 không chia hết cho 2 và cho 5;

2 002 có chữ số tận cùng là 2 nên 2 002 nên chia hết cho 2 nhưng không chia hết cho 5;

2 003 có chữ số tận cùng là 3 nên 2 003 không chia hết cho 2 và cho 5;

2 004 có chữ số tận cùng là 4 nên 2 004 chia hết cho 2 nhưng không chia hết cho 5;

2 005 có chữ số tận cùng là 5 nên 2 005 không chia hết cho 2 nhưng chia hết cho 5;

2 006 có chữ số tận cùng là 6 nên 2 006 chia hết cho 2 nhưng không chia hết cho 5;

2 007 có chữ số tận cùng là 7 nên 2 007 không chia hết cho 2 và cho 5;

2 008 có chữ số tận cùng là 8 nên 2 008 chia hết cho 2 nhưng không chia hết cho 5;

2 009 có chữ số tân cùng là 9 nên 2 009 không chia hết cho 2 và cho 5.

a) Số chia hết cho 2 là: 2 000; 2 002; 2 004; 2 006; 2 008.

b) Số chia hết cho 5 là: 2 000; 2 005.

c) Vì số 2 000 đều chia hết cho 2 và 5 nên 2 000 chia hết cho 10.

Bài 2 trang 21 sách bài tập Toán lớp 6 Tập 1: Tìm số thích hợp thay cho dấu * để số  thỏa mãn điều kiện: ....

a) Chia hết cho 2

b) Chia hết cho 5

c) Chia hết cho cả 2 và 5.

Lời giải:

a) Để số 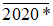 chia hết cho 2 thì chữ số tận cùng của số này phải là một số chẵn có một chữ số, nghĩa là:

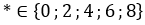
Vậy với 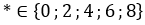 thì số  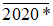chia hết cho 2.

b) Để số 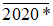 chia hết cho 5 thì chữ số tận cùng của số này phải là 0 hoặc 5, nghĩa là:

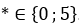
Vậy với 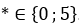 thì số  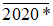chia hết cho 5.

c) Để số 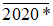 chia hết cho 10 thì số này vừa phải chia hết cho 2 vừa phải chia hết cho 5.

Khi đó * = 0.

Vậy với * = 0 thì số 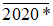 chia hết cho 10.

Bài 3 trang 21 sách bài tập Toán lớp 6 Tập 1: Có hay không?

a) Tích của hai số chia hết cho 2 là một số chia hết cho 5

b) Tích của hai số chia hết cho 5 là một số chia hết cho 2.

c) Tích của một số chia hết cho 2 và một số chia hết cho 5 là một số chia hết cho 10.

Lời giải:

a) Có tồn tại tích của hai số chia hết cho 2, chẳng hạn:

Hai số chia hết cho 2 là 10 và 16 thì tích là 10.16 = 160 là một số có chữ số tận cùng là 0 nên chia hết cho 5.

b) Có tồn tại tích của hai số chia hết cho 5 là một số chia hết cho 2, chẳng hạn:

Hai số chia hết cho 5 là 30 và 5 thì tích là 30.5 = 150 là một số có chữ số tận cùng là 0 nên chia hết cho 2.

c) Có tồn tại (luôn tồn tại) tích của một số chia hết cho 2 và một số chia hết cho 5 là một số chia hết cho 10, chẳng hạn:

Số chia hết cho 2 là 48 và số chia hết cho 5 là 25 thì tích 48.25 = 1 200 là một số chia hết cho 10.

Bài 4 trang 21 sách bài tập Toán lớp 6 Tập 1: Có thể chia đều 20 quả cam, 28 quả quýt và 10 quả xoài vào 5 túi mà không cần cắt quả nào không?

Lời giải:

Ta có 20 có chữ số tận cùng là 0 nên 20 chia hết cho 5. Do đó có thể chia đều 20 quả cam vào 5 túi.

10 có chữ số tận cùng là 0 nên 10 chia hết cho 5. Do đó có thể chia đều 10 quả xoài vào 5 túi.

Riêng 28 có chữ số tận cùng là 8 nên 28 không chia hết cho 5. Do đó không thể chia đều 28 quả quýt vào 5 túi.

Vậy không thể chia đều 20 quả cam, 28 quả quýt và 10 quả xoài vào 5 túi mà không cần cắt quả nào.

Lý thuyết Dấu hiệu chia hết cho 2, cho 5

1. Dấu hiệu chia hết cho 2

Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

Ví dụ:

a) Số 15 552 chia hết cho 2 vì có chữ số tận cùng là 2.

b) Số 955 không chia hết cho 2 vì có chữ số tận cùng là 5 (5 không là số chẵn).

2. Dấu hiệu chia hết cho 5

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

Ví dụ: Xét số 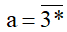 . Thay * bởi số nào thì a chia hết cho 5, bởi số nào thì a không chia hết cho 5?

Hướng dẫn giải

Chữ số tận cùng của a là ∗ nên để a chia hết cho 5 thì ∗ phải là 0 hoặc 5.

Để a không chia hết cho 5 thì ∗ phải khác 0 hoặc 5, tức là các số 1; 2; 3; 4; 6; 7; 8; 9.

Vậy thay ∗ bằng 1; 2; 3; 4; 6; 7; 8; 9 thì a không chia hết cho 5.