Với giải sách bài tập Toán 6 Bài 4: Hình thang cân sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 4: Hình thang cân

Bài 26 trang 112 sách bài tập Toán lớp 6 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Hình thang cân có hai cạnh bên bằng nhau và hai đường chéo bằng nhau.

b) Hình thang cân có hai cạnh bên bằng nhau và hai đường chéo không bằng nhau.

c) Có vô số hình thang cân mà độ dài đáy lớn gấp hai lần độ dài đáy bé.

Lời giải:

Phát biểu a) là pháp biểu đúng.

Phát biểu b) là sai vì hai đường chéo của hình thang cân bằng nhau.

Phát biểu c) là đúng.

Bài 27 trang 113 sách bài tập Toán lớp 6 Tập 1: Trong Hình 29, các hình từ a) đến e), hình nào là hình thang cân?

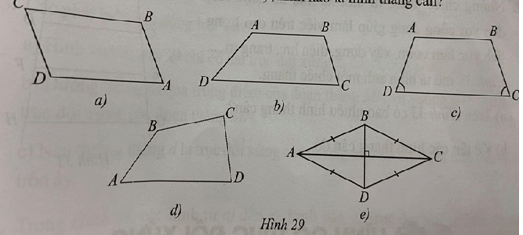
Lời giải:

Trong các hình đã cho, hình 29c) là hình thang cân vì có hai đáy song song và có hai góc kề một đáy bằng nhau.

Bài 28 trang 113 sách bài tập Toán lớp 6 Tập 1: Cho hình thang cân ABCD với độ dài cạnh đáy AB = 6cm. Trung bình cộng của hai đáy bằng 9cm. Độ dài cạnh bên kém độ dài cạnh đáy CD là 7cm (Hình 30). Tính chu vi của hình thang cân ABCD.

                  Hình 30

Lời giải:

Độ dài cạnh CD là: 9.2 – 6 = 18 – 6 = 12 cm.

Độ dài hai cạnh bên AD bằng CB và bằng: 12 – 7 = 5 cm.

Chu vi hình thang cân ABCD là: 6 + 5 + 12 + 5 = 28 cm.

Vậy chu vi hình thang cân ABCD là 28cm.

Bài 29 trang 113 sách bài tập Toán lớp 6 Tập 1: Cho hình thang cân MNPQ với trung bình cộng của hai đáy bằng 10cm. Đáy lớn dài hơn đáy nhỏ 8cm. Độ dài chiều cao hơn độ dài đáy nhỏ 2cm. Tính diện tích hình thang cân MNPQ.

Lời giải:

Tổng độ dài hai đáy là: 10.2 = 20 (cm).

Độ dài đáy nhỏ của là: (10.2 – 8):2 = 6 (cm).

Độ dài đáy lớn là: 6 + 8 = 14 (cm).

Chiều cao là: 6 + 2 = 8 (cm).

Diện tích hình thang cân MNPQ là: (6 + 14).8:2 = 80 (cm²).

Vậy diện tích hình thang cân MNPQ là: 80 cm².

Bài 30 trang 113 sách bài tập Toán lớp 6 Tập 1: Cho hình thang cân ABCD, biết mỗi ô vuông có cạnh 1cm (Hình 31).

a) Tính diện tích hình thang cân ABCD.

b) Diện tích tam giác BDC gấp mấy lần diện tích tam giác ADE?

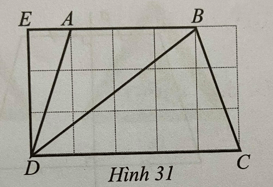
Lời giải:

a)

Độ dài đáy lớn CD là: 5 cm.

Độ dài đáy nhỏ AB là: 3 cm.

Chiều cao của hình thang ABCD bằng cạnh ED bằng 3 cm.

Diện tích hình thang ABCD là: (5 + 3).3:2 = 12 cm².

b)

Tam giác BCD có đáy CD bằng 5cm và chiều cao bằng cạnh ED bằng 3cm.

Tam giác ADE có đáy AE bằng 1 cm và chiều cao là ED bằng 3cm.

Vậy diện tích tam giác BCD gấp 5 lần diện tích tam giác ADE.

Bài 31 trang 113 sách bài tập Toán lớp 6 Tập 1: Bác Đức dự định mua loại gỗ giá 100 đồng/cm² để làm một chiếc bàn như Hình 32. Mặt bàn là một hình thang cân có các đáy lần lượt là 90cm, 120cm và chiều cao 80cm. Hãy tính giúp bác Đức số tiền mua gỗ để đóng mặt bàn đó.

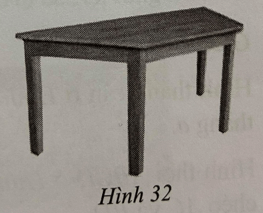
Lời giải:

Diện tích mặt bàn là: (90 + 120).80:2 = 8 400 (cm²).

Số tiền mua gỗ để đóng mặt bàn đó: 8 400. 100 = 840 000 (đồng).

Vậy bác Đức cần 8 400 000 đồng mua gỗ để đóng mặt bàn đó.

Bài 32 trang 114 sách bài tập Toán lớp 6 Tập 1: Những chiếc thang từ thời xa xưa đã được biết đến với công dụng giúp làm việc trên cao trong lĩnh vực làm vườn, xây dựng, điện lực, trang trí, … Hình 33 mô tả hình ảnh một chiếc thang.

a) Trên Hình 33 có bao nhiêu hình thang cân?

b) Kể tên các hình thang cân đó.

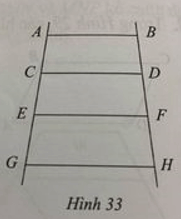
Lời giải:

a) Có tất cả 6 hình thang cân.

b) Các hình thang cân là: ABCD, ABFE, ABHG, CDFE, CDHG, EFHG.

Lý thuyết Hình thang cân

I. Nhận biết Hình thang cân

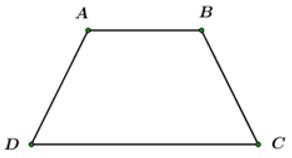
Cho Hình thang cân ABCD

Khi đó Hình thang cân ABCD có:

+ Hai cạnh đáy AB và CD song song với nhau;

+ Hai cạnh bên bằng nhau: AD = BC; hai đường chéo bằng nhau: AC = BD;

+ Hai góc kề với đáy AB bằng nhau, tức là hai góc DAB và CBA bằng nhau; hai góc kề với đáy CD bằng nhau, tức là hai góc ADC và góc BCD bằng nhau. 

II. Chu vi và diện tích Hình thang cân

(Hình thang cân có hai cạnh bên bằng nhau)

- Chu vi của Hình thang cân bằng tổng độ dài các cạnh của Hình thang cân đó

C = a + b + c + c = a + b + 2c

- Diện tích của Hình thang cân bằng tổng độ dài hai cạnh đáy nhân với chiều cao rồi chia đôi

 $S=\frac{\left(a+b\right).h}{2}$.