Với giải bài tập Toán lớp 6 Bài 4: Hình thang cân chi tiết bám sát nội dung sgk Toán 6 Tập 1 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:

Giải bài tập Toán 6 Bài 4: Hình thang cân

Trả lời câu hỏi giữa bài

Giải Toán 6 trang 105 Tập 1 Cánh diều

Hoạt động 1 trang 105 Toán lớp 6 Tập 1:

Lời giải:

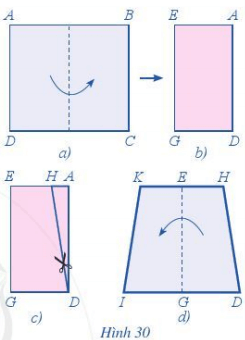
a) Gấp miếng bìa có dạng hình chữ nhật ABCD sao cho đỉnh A trùng với đỉnh B; đỉnh D trùng với đỉnh C (Xem Hình 30a).

Ta nhận được miếng bìa EADG ở Hình 30b.

b) Cắt đi miếng bìa hình tam giác ADH từ miếng bìa EADG (xem Hình 30c).

c) Trải miếng bìa còn lại để nhận được miếng bìa có dạng hình thang KHDI (xem Hình 30d).

d) Vẽ đường viền xung quanh miếng bìa KHDI để nhận được hình thang KHDI. Hình thang đó gọi là hình thang cân.

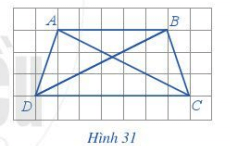
Hoạt động 2 trang 105 Toán lớp 6 Tập 1: Với hình thang cân ABCD ở Hình 31, thực hiện hoạt động sau:

a) Quan sát hai cạnh đáy AB và CD có song song với nhau không.

b) Sử dụng thước thẳng (có chia đơn vị) để đo độ dài các cạnh AD và BC, độ dài các đường chéo AC và BD.

c) Gấp hình thang cân ABCD sao cho cạnh AD trùng với cạnh BC, đỉnh A trùng với đỉnh B, đỉnh D trùng với đỉnh C (Hình 32). 

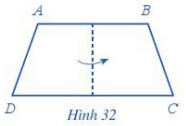
So sánh góc DAB và góc CBA; góc ADC và góc BCD.  

Lời giải:

a) Hai cạnh đáy AB và CD song song với nhau.

b) Sau khi đo độ dài, ta thấy các cạnh AD và BC bằng nhau, đường chéo AC và BD bằng nhau.

c) Khi gấp hình ta thấy góc DAB trùng với góc CBA và góc ADC trùng với góc BCD. 

Do đó góc DAB và góc CBA bằng nhau, góc ADC và góc BCD bằng nhau. 

Giải Toán 6 trang 106 Tập 1 Cánh diều

Luyện tập 1 trang 106 Toán lớp 6 Tập 1: Cho hình thang cân PQRS có độ dài đáy PQ = 10 cm, đáy RS ngắn hơn đáy PQ là 6 cm, độ dài cạnh bên PS bằng một nửa độ dài đáy PQ. Tính chu vi của hình thang cân PQRS.

Lời giải:

Đáy RS ngắn hơn đáy PQ là 6 cm nên độ dài đáy RS là: 

10 – 6 = 4 (cm)

Độ dài cạnh bên PS bằng một nửa độ dài đáy PQ nên độ dài cạnh bên PS là:

10 : 2 = 5 (cm)

Vì PQRS là hình thang cân nên hai cạnh bên PS và QR bằng nhau 

Nên QR = PS = 5 cm.

Chu vi của hình thang cân PQRS là: 

PQ + RS + QR + PS = 10 + 4 + 5 + 5 = 24 (cm)

Vậy chu vi của hình thang PQRS là 24 cm.

Bài tập

Bài 1 trang 106 Toán lớp 6 Tập 1: Với một lần cắt hoặc gấp, hãy tạo ra hình thang cân từ:

a) Mảnh bìa có dạng hình tam giác đều;

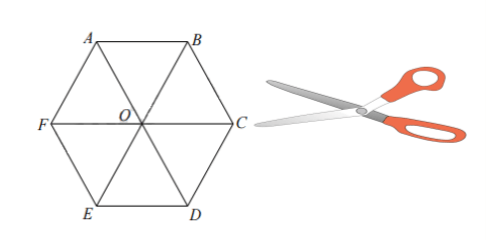
b) Mảnh bìa có dạng hình lục giác đều.

Lời giải:

a) Ta cắt hoặc gấp mảnh bìa hình tam giác đều theo một đường thẳng đi qua hai cạnh và song song với cạnh còn lại của hình tam giác đó, ta được hình thang cân.

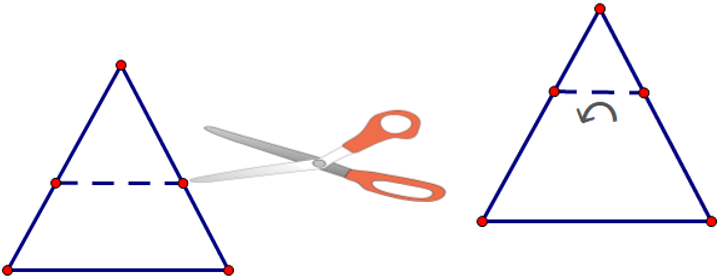
b) Ta cắt hoặc gấp mảnh bìa hình lục giác đều theo một đường chéo chính FC (hoặc AD hoặc BE) ta được hình thang cân. 

Bài 2 trang 106 Toán lớp 6 Tập 1: Cho hình thang cân ABCD có độ dài đáy AB bằng 4 cm, độ dài đáy CD gấp đôi độ dài đáy AB, độ dài chiều cao AH bằng 3 cm. Tính diện tích hình thang cân ABCD.

Lời giải:

Độ dài đáy CD gấp đôi độ dài đáy AB nên độ dài đáy CD là: 

4 . 2 = 8 (cm)

Ta có: AB = 4 cm; CD = 8 cm; AH = 3 cm. Do đó diện tích hình thang cân ABCD là: 

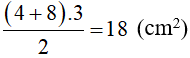
Vậy diện tích hình thang cân ABCD là 18 cm².

Giải Toán 6 trang 107 Tập 1 Cánh diều

Bài 3 trang 107 Toán lớp 6 Tập 1: Người ta làm một cái chụp đèn có bốn mặt giống nhau, mỗi mặt có dạng hình thang cân (Hình 35).

Trong đó, khung của mỗi mặt được cấu tạo bởi các đoạn ống trúc nhỏ, đoạn ống trúc để làm các cạnh đáy lớn dài 20 cm, đoạn ống trúc để làm các cạnh đáy nhỏ dài 12 cm và đoạn ống trúc để làm các cạnh bên dài 30 cm. Hãy tính tổng độ dài của các đoạn ống trúc dùng làm một chiếc chụp đèn như thế.

Lời giải:

Quan sát Hình 35, ta thấy mỗi mặt của đèn là một hình thang cân có độ dài đáy lớn là 20 cm, đáy nhỏ là 12 cm, cạnh bên là 30 cm. Lại có, mỗi cạnh bên của mỗi mặt đèn hình thang cân lại là cạnh bên chung cho hai mặt của chụp đèn đó. 

Do đó, ta cần 4 đoạn ống trúc để làm cạnh bên; 4 đoạn ống trúc để làm đáy nhỏ và 4 đoạn ống trúc để làm đáy lớn. 

Nên tổng độ dài các đoạn ống trúc dùng làm một chiếc chụp đèn là: 

30 . 4 + 12 . 4 + 20 . 4 = 248 (cm)

Vậy tổng độ dài các đoạn ống trúc dùng làm một chiếc chụp đèn theo yêu cầu của đề bài là 248 cm.

Lý thuyết Hình thang cân

I. Nhận biết Hình thang cân

Cho Hình thang cân ABCD

Khi đó Hình thang cân ABCD có:

+ Hai cạnh đáy AB và CD song song với nhau;

+ Hai cạnh bên bằng nhau: AD = BC; hai đường chéo bằng nhau: AC = BD;

+ Hai góc kề với đáy AB bằng nhau, tức là hai góc DAB và CBA bằng nhau; hai góc kề với đáy CD bằng nhau, tức là hai góc ADC và góc BCD bằng nhau. 

II. Chu vi và diện tích Hình thang cân

(Hình thang cân có hai cạnh bên bằng nhau)

- Chu vi của Hình thang cân bằng tổng độ dài các cạnh của Hình thang cân đó

C = a + b + c + c = a + b + 2c

- Diện tích của Hình thang cân bằng tổng độ dài hai cạnh đáy nhân với chiều cao rồi chia đôi

 $S=\frac{\left(a+b\right).h}{2}$.

Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:

Bài 3: Hình bình hành

Bài 5: Hình có trục đối xứng

Bài 6: Hình có tâm đối xứng

Bài 7: Đối xứng trong thực tiễn