Với giải sách bài tập Toán 6 Bài 6: Thứ tự thực hiện các phép tính sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 6: Phép chia hết hai số nguyên - Quan hệ chia hết trong tập hợp số nguyên

Bài 51 trang 85 sách bài tập Toán lớp 6 Tập 1: Thực hiện phép tính:

a) (-56):7; 

b) (-132).(-98):11;

c) [900 + (-1 140) + 720] : (-120); 

d) [299.(-74) + (-299).(-24)]: (-50);

e) 6.(-4²).(-10²):2⁴; 

f) [(-9).(-9).(-9) + 9³]:8¹⁰.

Lời giải:

a) (-56):7

= -(56:7)

= -8.                                                   

b) (-132).(-98):11

= 12 936:11

= 1 176.

c) [900 + (-1 140) + 720] : (-120)

= [(-240) + 720] : (-120)

=  480: (-120)

= -4.  

d) [299.(-74) + (-299).(-24)]: (-50)

= [299.(-74) + 299.24] : (-50)

= 299[(-74) + 24] : (-50)

= 299.(-50): (-50)

= 299

e) 6.(-4²).(-10²):2⁴

= 6.(-16).(-100):16

= 6.(-100)(-16):16

= (-600).(-1)

= 600.                    

f) [(-9).(-9).(-9) + 9³]:8¹⁰

= [-9³ + 9³]:8¹⁰

= 0: 8¹⁰

= 0.

Bài 52 trang 85 sách bài tập Toán lớp 6 Tập 1: Cho a, b (b  0) là các số nguyên và a chia hết cho b. Điền các dấu “+”, “-“ thích hợp cho :

Lời giải:

+) a mang dấu dương, b mang dấu âm thì a và b khác dấu. Do đó thương a:b mang dấu âm.

+) a mang dấu âm, b mang dấu dương thì a và b khác dấu. Do đó thương a:b mang dấu âm.

+) a và b đều mang dấu âm nên a và b cùng dấu. Do đó thương a:b mang dấu dương.

+) a và b đều mang dấu dương nên a và b cùng dấu. Do đó thương a:b mang dấu dương.

Ta có bảng sau:

Bài 53 trang 85 sách bài tập Toán lớp 6 Tập 1: Chọn dấu “>”, “<”, “=” thích hợp :

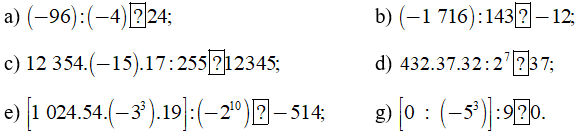
Lời giải:

a) Ta có: (-96) : (-4) = 24. Do đó, ta viết: (-96):(-4)  24

b) Ta có: (-1 716):143 = -(1 716:143) = -12. Do đó, ta viết: (-1716):143  -12

c) Ta có: 12 354.(-15).17:255 là một số âm nên 12 354.(-15).17:255 < 12 345. Do đó ta viết: 12354.(-15).17:255  12345

d) Ta có: 432.37.32:2⁷ 

= 108.4.37.2⁵:2⁷ 

= 108.2².37.2⁵:2⁷ 

= 108.37.2².2⁵:2⁷ 

= 108.37.2⁷:2⁷

= 108.37 > 37. 

Hay 432.37.32:2⁷ > 37.

Do đó, ta viết: 432.37.32:2⁷ 37

e) Ta có: [1024.54.(-3)³.19]:(-2¹⁰)

= [2¹⁰.54.(-3)³.19] : (-2¹⁰)

= [54.(-3³).19].2¹⁰ : (-2¹⁰)

= [54.(-27).19(-1)

= 54.27.19 > 0 > -514

Do đó, ta viết:  [1024.54.(-3)³.19]:(-2¹⁰)  - 514

g) Ta có [0 : (-5³)] : 9 = [0 : (-125)] : 9 = 0 : 9 = 0

Do đó, ta viết: [0 : (-5³)] : 9 0

Bài 54 trang 86 sách bài tập Toán lớp 6 Tập 1: So sánh hai biểu thức sau mà không tính cụ thể giá trị của chúng:

a) (-200 200):20 + 20 và 2 020:20;

b) (9 876 – 6 789).(9 876 + 6 789) và – 134.

Lời giải:

a) Ta có: (-200 200):20 + 20 < 0 mà 2 020:20 > 0 nên (-200 200):20 + 20 < 2 020:20.

Vậy (-200 200):20 + 20 < 2 020:20.

b) Ta có: (9 876 – 6 789).(9 876 + 6 789) > 0 mà – 134 < 0 nên (9 876 – 6 789).(9 876 + 6 789) > -134.

Vậy (9 876 – 6 789).(9 876 + 6 789) > -134.

Bài 55 trang 86 sách bài tập Toán lớp 6 Tập 1: Tìm các số nguyên x, biết:

a) (-3).x = 264;

b) x + x + x + x = 900;

c) 100 : (x – 7) = 1;

d) (5x – 10) : (77x² + 1) = 0.

Lời giải:

a) (-3).x = 264

x = 264 : (-3)

x = -88.

Vậy x = -88.

b) x + x + x + x = 900

4x = 900

x = 900:4

x = 225.

Vậy x = 225.

c) 100 : (x – 7) = 1

x – 7 = 100:1

x – 7 = 100

x = 100 + 7

x = 107.

Vậy x = 107.

d) (5x – 10) : (77x² + 1) = 0

TH1: 5x – 10 = 0

5x = 10

x = 10:5

x = 2.

TH2: 77x² + 1 = 0

77x² = -1 (vô lí).

Vậy x = 2.

Bài 56 trang 86 sách bài tập Toán lớp 6 Tập 1: Người ta viết các số nguyên -1; -2; -3; …; -2 020; -2 021 vào các cột A, B, C, D, E, G, H như bảng sau:

Hỏi số - 2 021 nằm ở cột nào?

Lời giải:

Theo quy luật, các số ở cột A là -1; -14; -15; -28; -29; -42; -43; -56; …

Tính từ số -14, hai số cách nhau 1 hàng hơn kém nhau 14 đơn vị theo thứ giảm dần trong cùng một cột.

Do 2 002 = 14.143 nên số - 2 016 = (-14) – 2 002 nằm ở cột A và – 2017 nằm ở ô bên dưới cùng với cột với -2 016. Mà -2 021 = (- 2017) – 4 nên số - 2 021 nằm ở cột E.

Bài 57 trang 86 sách bài tập Toán lớp 6 Tập 1: Chỉ số đồng hồ đo nước sinh hoạt cuối các tháng 9, 10, 11, 12 của năm 2020 ở nhà bác Long được thống kê trong bảng sau:

Biết số tiền nước phải trả cho mỗi m³ là không đổi và tổng số tiền mà bác Long phải trả trong quý IV là 90 000 đồng. Tính số tiền nước mà bác Long phải trả của tháng 10 và thàng 11 năm 2020.

Lời giải:

Một năm có 12 tháng được chia làm 4 quý, trong đó:

Quý I gồm tháng 1, tháng 2, tháng 3;

Quý II gồm tháng 4, tháng 5, tháng 6;

Quý III gồm tháng 7, tháng 8, tháng 9;

Quý IV gồm tháng 10, tháng 11, tháng 12.

Số m³ nước của nhà bác Long đã sử dụng trong ba tháng cuối năm (hay trong quý IV) là: 

37 – 22 = 15 (số).

Mỗi m³ nước có giá tiền là: 90 000:15 = 6 000 (m³).

Số m³ nước bác Long đã sử dụng trong tháng 10 là: 26 – 22 = 4 (m³).

Số tiền nước mà bác Long phải trả của tháng 10 năm 2020 là:

4.6 000 = 24 000 (đồng).

Số m³ nước bác Long đã sử dụng trong tháng 11 là: 31 – 26 = 5 (m³).

Số tiền nước mà bác Long phải trả của tháng 11 năm 2020 là:

5.6 000 = 30 000 (đồng).

Vậy số tiền nước mà bác Long phải trả của tháng 10 và tháng 11 năm 2020 lần lượt là 24 000 đồng và 30 000 đồng.

Bài 58 trang 86 sách bài tập Toán lớp 6 Tập 1: Một công ty cơ khí sản xuất đồ dùng dân dụng đã đề xuất chế độ thưởng phạt như bảng sau:

Bác Toàn làm được 40 sản phẩm loại A, 35 sản phẩm loại B, 15 sản phẩm loại C và 10 sản phẩm loại D. Vậy bác Toàn được thưởng hay phạt trung bình bao nhiêu tiền trên mỗi sản phẩm.

Lời giải:

Số tiền bác Toàn được nhận là: 40.100 000 + 35.50 000 – 15.30 000 – 10.70 000

= 4 000 000 + 1 750 000 – 450 000 – 700 000

= 4 600 000 (đồng).

Tổng số sản phẩm bác Toàn làm được là: 40 + 35 + 15 + 10 = 100 (sản phẩm).

Do đó bác Toàn được thưởng trung bình mỗi sản phẩm là: 

4 600 000:100 = 46 000 (đồng).

Vậy bác Toàn được thưởng trung bình 46 000 đồng trên mỗi sản phẩm.

Bài 59 trang 87 sách bài tập Toán lớp 6 Tập 1: Bạn Nam có một bộ sưu tập gồm 169 quyển truyện khác nhau và muốn tặng bạn bè, biết không có hai bạn nào nhận được số quyển truyện bằng nhau. Bạn Nam có thể tặng được nhiều nhất cho bao nhiêu bạn?

Lời giải:

Giả sử Nam tặng 169 quyển truyện được nhiều nhất cho n bạn. Không có hai bạn nào nhận được số quyển truyện bằng nhau, nên để chia được cho nhiều bạn nhất thì phải chia cho từng bạn số quyển truyện tương ứng là: 1; 2; 3; 4; 5; …; n – 1; n.

Tổng số quyển truyện của n bạn trên là: 

1 + 2 + 3 + 4 + ..... + n - 1 + n = 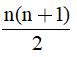 (quyển).

Nếu n ≥ 18 thì 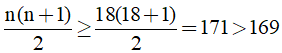 . Mà bạn Nam chỉ có 169 quyển truyện nên bạn Nam có thể tặng nhiều nhất cho 17 bạn.

Vậy bạn Nam có thể chia 169 quyển truyện cho nhiều nhất 17 bạn.

Bài 60 trang 87 sách bài tập Toán lớp 6 Tập 1: Tìm các số nguyên x, sao cho:

a) 11 chia hết cho x;

b) x chia hết cho 18;

c) 2x – 3 là bội của x + 1;

d) x – 2 là ước của 3x – 2.

Lời giải:

a) Vì 11 chia hết cho x nên x thuộc Ư(11) = {1; -1; 11; -11}.

Vậy x ∈ {1; -1; 11; -11}.

b) Vì x chia hết cho 18 nên x thuộc tập B(18) = {0; 18; 36; 54; …}.

Vậy x ∈ {0; 18; 36; 54; …}.

c) Ta có 2x – 3 = 2x + 2 – 5 = 2(x + 1) – 5

Vì 2x – 3 là bội của x + 1 nên 2x – 3 chia hết cho x + 1.

Mà 2(x + 1) chia hết cho x + 1 nên 5 phải chia hết cho x + 1 hay x + 1 thuộc Ư(5) = {1; -1; 5; -5}.

Suy ra x ∈ {0; -2; 4; -6}.

Vậy x ∈ {0; -2; 4; -6}.

d) Ta có x – 2 là ước của 3x – 2 nghĩa là 3x – 2 là bội của x – 2 hay 3x – 2 chia hết cho x – 2.

Ta lại có: 3x – 2 = 3x – 6 + 4 = 3(x – 2) + 4.

Mà 3(x – 2) chia hết cho x – 2 nên 4 cũng phải chia hết cho x – 2 hay x – 2 thuộc Ư(4) = {1; -1; 2; -2; 4; -4}.

Suy ra x ∈ {3; 1; 4; 0; 6; -2}.

Vậy x ∈ {3; 1; 4; 0; 6; -2}.

Lý thuyết Phép chia hết hai số nguyên. Quan hệ chia hết trong tập hợp số nguyên

I. Phép chia hết hai số nguyên khác dấu 

Để chia hai số nguyên khác dấu, ta làm như sau:

Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại

Bước 2. Tính thương của hai số nguyên dương nhận được ở Bước 1

Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có thương cần tìm.

Ví dụ: (– 24) : 4 = – (24 : 4) = – 6 

           45 : (– 9) = – (45 : 9) = – 5 

II. Phép chia hết hai số nguyên cùng dấu 

1. Phép chia hết hai số nguyên dương

Phép chia hết của một số nguyên dương cho một số nguyên dương là phép chia hết hai số tự nhiên với số chia khác 0. 

Ví dụ: 32 : 8 = 4; 10 : 2 = 5; …

2. Phép chia hết hai số nguyên âm 

Để chia hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ dấu “–” trước mỗi số

Bước 2. Tính thương của hai số nguyên dương nhận được ở Bước 1, ta có thương cần tìm.

Ví dụ: (– 12) : (– 3) = 12 : 3 = 4

           (– 100) : (– 20) = 100 : 20 = 5 

Chú ý:

• Cách nhận biết dấu của thương:

(+)  : (+) → (+)

(–) : (–) → (+)

(+) : (–) → (–)

(–) : (+) → (–)

• Thứ tự thực hiện các phép tính với số nguyên (trong biểu thức không chứa dấu ngoặc hoặc có chứa dấu ngoặc) cũng giống như thứ tự thực hiện các phép tính với số tự nhiên.

III. Quan hệ chia hết 

Cho hai số nguyên a, b với . Nếu có số nguyên q sao cho a = b . q thì ta nói:

• a chia hết cho b;

• a là bội của b;

• b là ước của a.

Ví dụ: Ta có: – 48 = 6 . (– 8) nên – 48 chia hết cho 6 hay – 48 là bội của 6 và 6 là ước của – 48.   

Chú ý: 

+ Nếu a là bội của b thì – a cũng là bội của b.

+ Nếu b là ước của a thì – b cũng là ước của a. 

Ví dụ: 6 chia hết cho 2 nên 6 là bội của 2, do đó – 6 cũng là bội của 2

           – 25 chia hết cho 5 nên 5 là ước của – 25, do đó – 5 cũng là ước của – 25.