Với giải sách bài tập Toán 6 Bài 2: Hình có tâm đối xứng sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 2: Hình có tâm đối xứng

Bài 1 trang 74 sách bài tập Toán lớp 6 Tập 2: Tìm tâm đối xứng của các hình sau (nếu có):

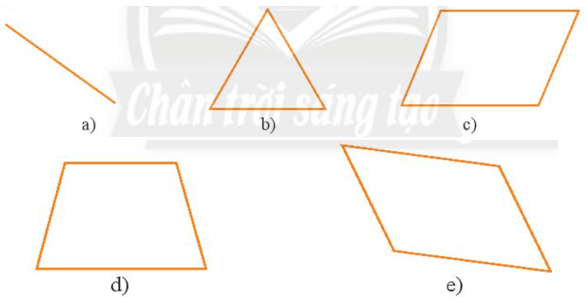
Lời giải:

Các hình a), c) và e) có tâm đối xứng, với tâm đối xứng được chỉ ra như hình vẽ.

Hình a)

Hình c)

Hình e)

Các hình b, d không có tâm đối xứng.

Bài 2 trang 74 sách bài tập Toán lớp 6 Tập 2: Vẽ thêm để được hình có tâm đối xứng là các điểm cho sẵn.

a) 

b) 

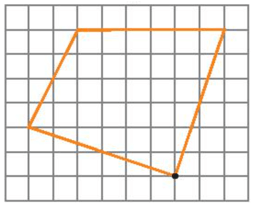
c) 

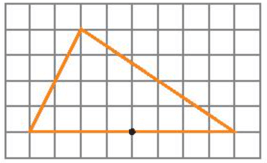
Lời giải:

Hình a) 

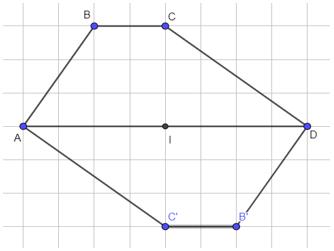
Đặt tên các đỉnh là A, B, C, D lần lượt như hình vẽ và I là tâm đối xứng:

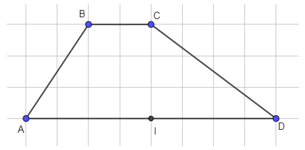
Ta thấy I là trung điểm AD, khi đó A đối xứng với D qua I.

Ta lấy các điểm B’, C’ lần lượt đối xứng với B, C qua I.

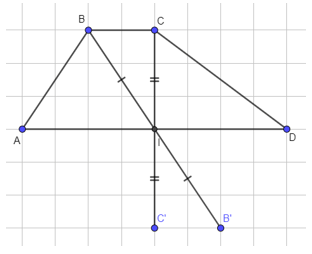
Nối các điểm lại, ta được hình ABCDB’C’ nhận I làm tâm đối xứng.

Hình b)

Đặt tên các đỉnh như hình vẽ là M, N, Q và tâm đối xứng là O.

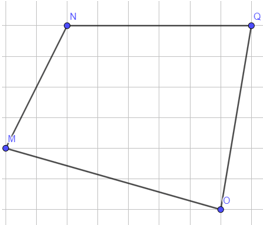
Ta lấy các điểm F, H, G lần lượt đối xứng với M, N, Q qua O, ta được:

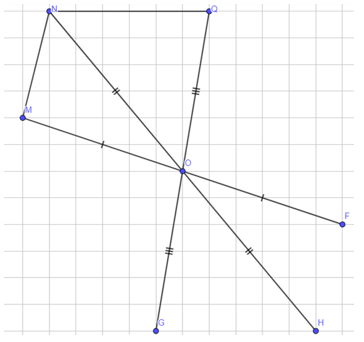
Nối các điểm F, H, G lại ta được hình nhận O là tâm đối xứng.

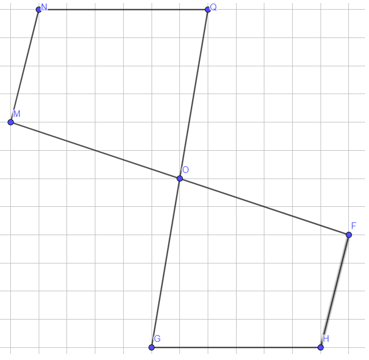
Hình c)

Đặt tên các đỉnh của hình vẽ lần lượt là X, Y, Z và tâm đối xứng là T.

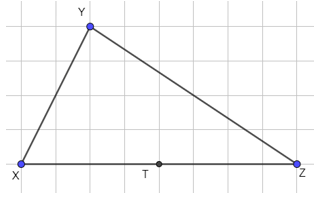
Ta thấy X và Z đối xứng với nhau qua T, ta lấy Y’ đối xứng với Y qua T, ta được:

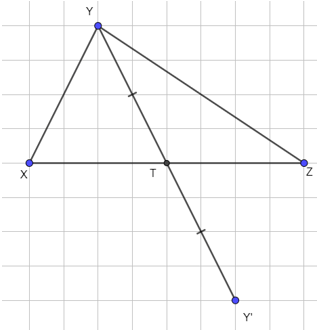
Nối X với Y’, Y’ với Z lại ta được hình nhận T làm tâm đối xứng.

Bài 3 trang 75 sách bài tập Toán lớp 6 Tập 2: Vẽ hình 6 cạnh có tâm đối xứng, không có trục đối xứng.

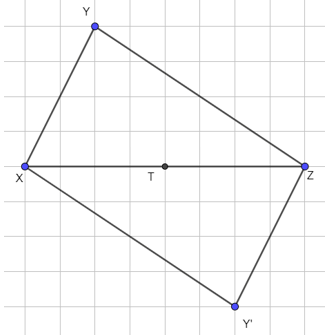
Lời giải:

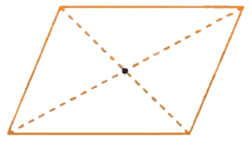
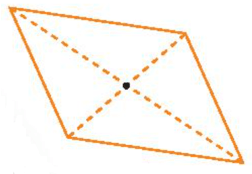
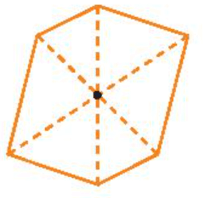
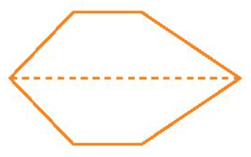
Hình dưới đây là hình 6 cạnh có tâm đối xứng, với tâm đối xứng là điểm giao của các đường nét đứt. Nhưng hình này không có trục đối xứng.

Bài 4 trang 75 sách bài tập Toán lớp 6 Tập 2: Vẽ hình 6 cạnh có trục đối xứng, không có tâm đối xứng.

Lời giải:

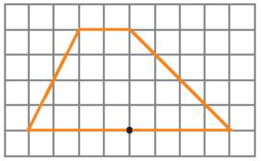
Hình dưới đây là hình 6 cạnh có trục đối xứng nhưng không có tâm đối xứng, với trục đối xứng là đường nét đứt.

Bài 5 trang 75 sách bài tập Toán lớp 6 Tập 2: Chữ cái nào sau đây có tâm đối xứng:

a) H A N O I;

b) N I N H B I N H;

c) C A M A U.

Lời giải:

Gập đôi hình sao cho hai phần trùng khít lên nhau, nếp đó chính là trục đối xứng.

I là tâm đối xứng của hình H nếu I là trung điểm của đoạn thẳng Nối hai điểm tương ứng bất kì trên H.

Vậy các chữ cái H, N, O, I có tâm đối xứng, các chữ cái còn lại không có tâm đối xứng.

Bài 6 trang 75 sách bài tập Toán lớp 6 Tập 2: Tìm vật dụng trong nhà em có tâm đối xứng.

Lời giải:

Hình tròn, hình chữ nhật, hình vuông, hình thoi, hình bình hành,… là những hình có tâm đối xứng.

Các vật dụng trong nhà có tâm đối xứng, ví dụ: mâm, đĩa, thớt, mặt bàn, bảng, quyển sách, cánh cửa,…

Bài 7 trang 75 sách bài tập Toán lớp 6 Tập 2: Tìm các dụng cụ lao động có trục đối xứng.

Lời giải:

Các dụng cụ lao động có hai nửa cân xứng thì có trục đối xứng .

Ví dụ:

Cái cuốc

Cái xẻng

Cái bay

Lý thuyết Hình có tâm đối xứng

Hình có tâm đối xứng. Tâm đối xứng

Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm Ota được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứngvà điểm O được gọi là tâm đối xứngcủa hình.

Ví dụ. Cho hình vẽ sau: Khi quay nửa vong quanh điểm O ta được vị trí mới chồng khít với vị trí ban đầu.

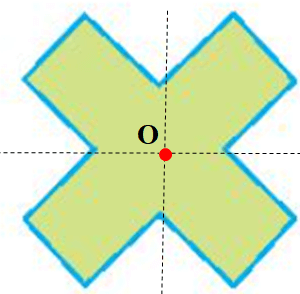
Khi đó, hình vẽ trên là hình có tâm đối xứng và O là tâm đối xứng của hình trên.