Với giải sách bài tập Toán 6 Bài 2: Thứ tự trong tập hợp số nguyên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 2: Thứ tự trong tập hợp số nguyên

Bài 1 trang 48 sách bài tập Toán lớp 6 Tập 1: So sánh các cặp số sau:

a) 16 và 25

b) -15 và 0

c) -36 và 3

d) -28 và -56

e) 13 và -100

g) -72 và -45

Lời giải:

a) Trên trục số điểm 16 nằm bên trái  điểm 25 nên 16 < 25;

b) Trên trục số điểm -15 nằm bên trái điểm 0 nên -15 < 0;

c) Trên trục số điểm -36 nằm bên trái điểm 3 nên -36 < 3;

d) Trên trục số điểm -56 nằm bên trái điểm – 28 nên -28 > -56;

e) Trên trục số điểm – 100 nằm bên trái điểm 13 nên 13 > -100;

g) Trên trục số điểm -72 nằm bên trái điểm – 45 nên -72 < -45.

Bài 2 trang 48 sách bài tập Toán lớp 6 Tập 1: Sắp xếp các số nguyên sau theo thứ tự tăng dần và ghi chúng lên một trục số:

6; 0; 5; -5; 1; -1; 3; -3; -6

Lời giải:

Ta sắp xếp các số nguyên theo thứ tự là: -6; -5; -3; -1; 0; 1; 3; 5; 6

Ta biểu diễn các số trên trục số :

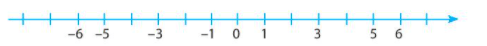
Bài 3 trang 48 sách bài tập Toán lớp 6 Tập 1: Hãy liệt kê các phần tử của mỗi tập hợp sau:

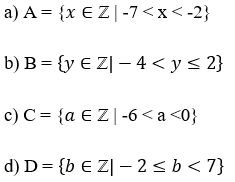
Lời giải:

a) Các số nguyên x thỏa mãn – 7 < x < -2 là: -6; -5; -4; -3.

Vậy A = {-6; -5; -4; -3}.

b) Các số nguyên y thỏa mãn -4 < y ≤ 2 là: -3; -2; -1; 0; 1; 2.

Vậy B = {-3; -2; -1; 0; 1; 2}.

c) Các số nguyên a thỏa mãn -6 < a < 0 là: -5; -4; -3; -2; -1.

Vậy C = {-5; -4; -3; -2; -1}.

d) Các số nguyên b thỏa mãn -2 < b ≤ 7 là: -2; -1; 0; 1; 2; 3; 4; 5; 6.

Vậy D = {-2; -1; 0; 1; 2; 3; 4; 5; 6}.

Bài 4 trang 49 sách bài tập Toán lớp 6 Tập 1: Nhiệt độ (độ C) cao nhất và thấp nhất trong một năm tại một địa điểm ở Canada (Ca-na-đa) được cho bởi bảng sau:

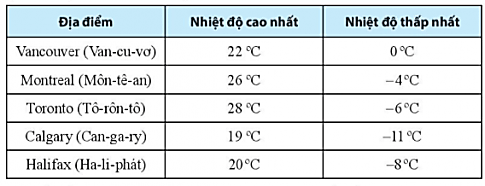
Hãy sắp xếp nhiệt độ trong bảng trên theo thứ tự từ thấp đến cao.

Lời giải:

Ta sắp xếp nhiệt độ trong bảng theo thứ tự từ thấp đến cao:

- 11⁰C; - 8⁰C; - 6⁰C; - 4⁰C; 0⁰C; 19⁰C; 20⁰C; 22⁰C; 26⁰C; 28⁰C.

Bài 5 trang 49 sách bài tập Toán lớp 6 Tập 1: Cho tập hợp A = {4; -3; 7; -12}

a) Viết tập hợp B bao gồm các phần tử A và các số đối của chúng.

b) Viết tập hợp C bao gồm các phần tử lớn hơn các phần tử của A một đơn vị.

Lời giải:

a) Số đối của 4 là: -4;

Số đối của – 3 là: 3;

Số đối của 7 là: - 7;

Số đối của -12 là 12;

Vậy B = {-4; -3; -7; -12; 4; 3; 7; 12}.

b) Các phần tử của A sau khi cộng thêm 1 đơn vị là: 5; -2; 8; -11.

Vậy C = {5; -2; 8; -11}.