Với giải bài tập Toán lớp 6 Bài 2: Thứ tự trong tập hợp số nguyên chi tiết bám sát nội dung sgk Toán 6 Tập 1 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 2: Thứ tự trong tập hợp số nguyên
Video giải Toán 6 Bài 2: Thứ tự trong tập hợp số nguyên - Chân trời sáng tạo
A. Các câu hỏi trong bài
Giải Toán 6 trang 54 Tập 1 Chân trời sáng tạo
Hoạt động khởi động trang 54 Toán lớp 6 Tập 1: Làm thế nào để so sánh hai số nguyên âm?
Lời giải:
Sau bài này chúng ta sẽ biết:
Để so sánh hai số nguyên âm a và b, ta có hai cách sau:
+ Trên trục số, nếu số a nằm bên trái số b thì a < b hoặc ngược lại.
+ Trong hai số nguyên âm a, b số nào có số đối lớn hơn thì số đó nhỏ hơn.
Lời giải:
Vì khi ta biểu diễn 2 số – 31 và – 7 lên trục số, ta thấy điểm biểu diễn số – 31 nằm bên trái điểm biểu diễn số – 7 nên -310C nhỏ hơn -70C nên nhiệt độ của Vostok sẽ thấp hơn nhiệt độ Ottawa.
Vậy trong tháng 1 tại Vostok sẽ lạnh hơn Ottawa.
Giải Toán 6 trang 55 Tập 1 Chân trời sáng tạo
Thực hành trang 55 Toán lớp 6 Tập 1: So sánh các cặp số nguyên sau:
a) – 10 và – 9; b) 2 và – 15;
c) 0 và – 3.
Lời giải:
a) Trên trục số, ta thấy số – 10 nằm ở bên trái số – 9 nên – 10 < - 9.
b) Trên trục số, ta thấy số – 15 nằm ở bên trái số 2 nên – 15 < 2 hay 2 > - 15.
c) Trên trục số, ta thấy số - 3 nằm bên trái số 0 nên – 3 < 0 hay 0 > - 3.
Vận dụng 1 trang 55 Toán lớp 6 Tập 1: Cho các số nguyên a, b, c sao cho:
a > 2; b < -7; - 1 < c < 1.
Hỏi trong các số nói trên, số nào là số nguyên dương, số nào là nguyên âm và số nào bằng 0?
Lời giải:
+) Vì a > 2, mà 2 > 0 nên a > 0 hay a là số nguyên dương.
+) Vì b < -7, mà – 7 < 0 nên b < 0 hay b là số nguyên âm.
+) Vì – 1 < c < 1, mà c là số nguyên nên c = 0.
Lời giải:
Ta xếp các số thành các nhóm rồi so sánh:
Nhóm 1: Các số nguyên âm: – 5 và – 2, ta có – 5 < – 2 < 0
Nhóm 2: Các số nguyên dương: 4 và 2, ta có 0 < 2 < 4
Do đó: – 5 < – 2 < 0 < 2 < 4
Sắp xếp các số trên theo thứ tự tăng dần ta được: – 5; – 2; 0; 2; 4.
Lời giải:
Bởi vì: - 180 (m) > - 1 000 (m) > - 4 000 (m) > - 6 000 (m)
Nên ta sắp xếp các sinh vật biển theo thứ tự giảm dần của độ cao của môi trường sống như sau: Cá cờ xanh (Blue marlin); Cá hố (Ribbon fish); Cá đèn (Lantern fish); Sao biển (Brittle fish).
B. Bài tập
Giải Toán 6 trang 56 Tập 1 Chân trời sáng tạo
Bài 1 trang 56 Toán lớp 6 Tập 1: So sánh các cặp số sau:
a) 6 và 5; b) – 5 và 0; c) – 6 và 5;
d) – 8 và – 6; e) 3 và – 10; g) – 2 và – 5.
Lời giải:
a) 6 > 5
b) – 5 < 0 (Số nguyên âm luôn nhỏ hơn 0)
c) – 6 < 5 (Số nguyên âm nhỏ hơn số nguyên dương)
d) – 8 < - 6 (Vì số đối của – 8 là 8 lớn hơn số đối của – 6 là 6)
e) 3 > - 10 (Số nguyên dương luôn lớn hơn số nguyên âm)
g) – 2 > - 5 (Vì số đối của – 2 là 2 nhỏ hơn số đối của – 5 là 5)
Bài 2 trang 56 Toán lớp 6 Tập 1: Tìm số đối của các số nguyên: 5; - 4; - 1; 0; 10; - 2 021.
Lời giải:
Số đối của 5 là - 5.
Số đối của – 4 là 4.
Số đối của – 1 là 1.
Số đối của 0 là 0.
Số đối của 10 là – 10.
Số đối của – 2 021 là 2021.
2; - 4; 6; 4; 8; 0; - 2; - 8; -6.
Lời giải:
* Ta chia các số đã cho thành các nhóm rồi so sánh:
Nhóm 1: Các số nguyên dương: 2; 6; 4; 8, ta có 0 < 2 < 4 < 6 < 8
Nhóm 2: Các số nguyên âm: – 4; – 2; – 6 ; – 8, ta có – 8 < – 6 < – 4 < – 2 < 0
Khi đó ta có: - 8 < - 6 < - 4 < - 2 < 0 < 2 < 4 < 6 < 8
Sắp xếp theo thứ tự tăng dần: - 8; - 6; - 4; - 2; 0; 2; 4; 6; 8.
* Biểu diễn các số nguyên đã cho trên trục số như sau:
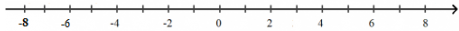
Bài 4 trang 56 Toán lớp 6 Tập 1: Hãy liệt kê các phần tử của mỗi tập hợp sau:
a) A = {a ∈Z | - 4 < a < - 1}; b) B = {b ∈Z | - 2 < b < 3};
c) C ={c ∈Z | - 3 < c < 0}; d) D ={d ∈Z | - 1 < d < 6}.
Lời giải:
a) Các số nguyên thỏa mãn lớn hơn -4 và nhỏ hơn -1 là: -3; -2.
Vậy A = {- 3; - 2}.
b) Các số nguyên thỏa mãn lớn hơn -2 và nhỏ hơn 3 là: -1; 0; 1; 2.
Vậy B = {- 1; 0; 1; 2}.
c) Các số nguyên thỏa mãn lớn hơn – 3 và nhỏ hơn 0 là: -2; -1.
Vậy C = {- 2; -1}.
d) Các số nguyên thỏa mãn lớn hơn -1 và nhỏ hơn 6 là: 0; 1; 2; 3; 4; 5.
Vậy D = {0; 1; 2; 3; 4; 5}.
Lời giải:
Ta so sánh và sắp xếp theo thứ tự từ thấp đến cao nhiệt độ như sau:
-510C < -150C < -20C < 80C < 120C
Vậy các địa điểm có nhiệt độ theo thứ tự từ thấp đến cao lần lượt là: Alaska (A-la-xca); New York (Niu Oóc); Montana (Mon– ta–na); Florida (Phlo-ra-đa); Hawaii (Ha–oai).
Lý thuyết Thứ tự trong tập hợp số nguyên
1. So sánh hai số nguyên
Khi biểu diễn hai số nguyên a, b trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì ta nói a nhỏ hơn b hoặc b lớn hơn a và ghi là: a < b hoặc b > a.
Ví dụ:
Số −4 nằm bên trái số −2 nên ta nói −4 nhỏ hơn −2 và ghi là −4 < −2, hoặc ta nói −4 lớn hơn −2 và ghi −4 > −2.
Nhận xét:
− Mọi số nguyên dương đều lớn hơn 0.
− Mọi số nguyên âm đều nhỏ hơn 0.
− Mọi số nguyên âm đều nhỏ hơn bất kì số nguyên dương nào.
− Với hai số nguyên âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.
Ví dụ: So sánh các cặp số sau:
a) 5 và −20;
b) −16 và −4.
Hướng dẫn giải
a) 5 là số nguyên dương và −20 là số nguyên âm nên 5 > −20.
Vậy 5 > −20.
b) Số đối của số −16 và −4 lần lượt là 16 và 4.
Vì 16 > 4 nên −16 < −4.
Vậy −16 < −4.
2. Thứ tự trong tập hợp số nguyên
Ví dụ: Sắp xếp các số − 5; 4; −2; 0; 2 theo thứ tự tăng dần.
Hướng dẫn giải
Ta xếp các số thành các nhóm rồi so sánh:
Nhóm 1: Các số nguyên âm: – 5 và – 2.
Số đối của – 5 và – 2 lần lượt là 5 và 2.
Vì 5 > 2 nên – 5 < – 2.
Do đó – 5 < – 2 < 0.
Nhóm 2: Các số nguyên dương: 4 và 2.
Ta có 2 < 4. Khi đó 0 < 2 < 4.
Do đó: – 5 < – 2 < 0 < 2 < 4.
Vậy các số đã cho được sắp xếp theo thứ tự tăng dần là: –5; –2; 0; 2; 4.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Số nguyên âm và tập hợp các số nguyên
Bài 3: Phép cộng và phép trừ hai số nguyên
Bài 4: Phép nhân và phép chia hết hai số nguyên
Bài 5: Hoạt động thực hành và trải nghiệm: Vui cùng số nguyên
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
