Với giải sách bài tập Toán 6 Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa một số nguyên tố sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa một số nguyên tố
Bài 1 trang 28 sách bài tập Toán lớp 6 Tập 1: Gọi P là tập hợp các số nguyên tố.
Điền kí hiệu ∈, ∉ thích hợp vào chỗ chấm.
41 … P;
57 … P;
83 … P;
95 … P.
Lời giải:
41 chỉ có hai ước là 1 và chính nó nên 41 là số nguyên tố. Suy ra 41∈P.
57 có tổng các chữ số là: 5 + 7 = 12 chia hết cho 3 nên 57 chia hết 3, nghĩa là 57 có nhiều hai ước nên 57 là hợp số. Suy ra 57∉ P.
83 chỉ có hai ước là 1 và chính nó nên 83 là số nguyên tố. Suy ra 83∈ P.
95 có chữ số tận cùng là 5 nên 95 chia hết cho 5, nghĩa là 95 có nhiều hơn hai ước nên 95 là hợp số. Suy ra 95∉ P.
117; 131; 313; 469; 647.
Lời giải:
Quan sát vào bảng nguyên tố, ta thấy các số nguyên tố là: 131; 313; 647.
Bài 3 trang 28 sách bài tập Toán lớp 6 Tập 1: Thay chữ số thích hợp vào dấu * để được mỗi số sau là:
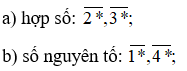
Lời giải:
|
Kết luận |
Đáp số |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
|
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
|
|
iii. Tổng của hai hợp số luôn là một hợp số. |
|
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
|
b) Với mỗi kết luận sai trong câu a, hãy cho ví dụ minh hoạ.
Lời giải:
a) - Tất cả mọi số chẵn lớn hơn 2 đều là hợp số. Do đó i) đúng.
- Mọi số nguyên tố lớn hơn 2 đều là các số lẻ. Mà tổng hai số lẻ này là một số chẵn lớn hơn 2 nên tổng hai số nguyên tố lớn hơn 2 này chia hết cho 2. Do đó chúng có nhiều hơn hai ước và là một hợp số. Suy ra ii) là đúng.
- Hai hợp số là 25 và 12 có tổng là 25 + 12 = 37 là một số nguyên tố. Do đó iii) là sai.
- Vì có một số nguyên tố chẵn duy nhất là 2 nên tích của số 2 với bất kì số nguyên tố nào khác đều là số chẵn. Chẳng hạn như tích của 2 và của 17 là 2.17 = 34 là một số chẵn. Do đó iv) đúng.
Ta có bảng sau:
|
Kết luận |
Đáp số |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
Đ |
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
Đ |
|
iii. Tổng của hai hợp số luôn là một hợp số. |
S |
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
Đ |
b) Ví dụ minh họa:
Hai hợp số là 25 và 12 có tổng là 25 + 12 = 37 là một số nguyên tố. Do đó iii) là sai.
b) Viết 15 thành tổng của 3 số nguyên tố.
Lời giải:
a) Ta có: 16 = 5 + 11 = 3 + 13;
18 = 5 + 13 = 7 + 11 ;
20 = 3 + 17 = 7 + 13
b) Ta có: 15 = 3 + 5 + 7
a) 154;
b) 187;
c) 630.
Lời giải:
a) Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc:
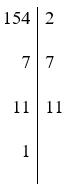
Vậy 154 = 2.7.11.
Cách 2: Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây:
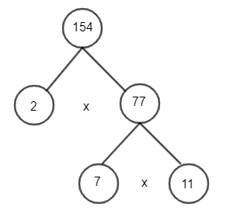
Vậy 154 = 2.7.11.
b) Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc:
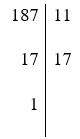
Vậy 187 = 11.17
Cách 2: Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây:
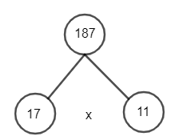
Vậy 187 = 11.17.
c) Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc:
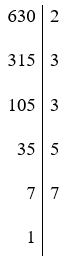
Vậy 630 = 2.32.5.7.
Cách 2: Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây:
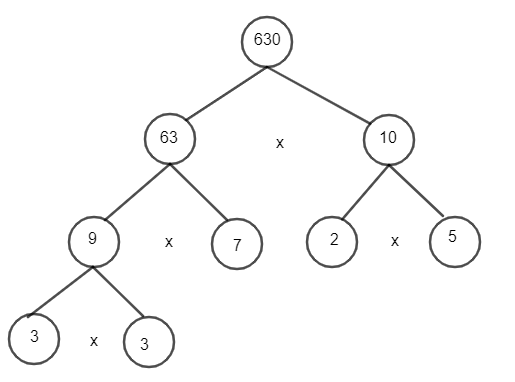
Vậy 630 = 2.32.5.7.
a) 38;
b) 75;
c) 100.
Lời giải:
a) 38 = 2.19
Tập hợp các ước của 38 là: {1; 2; 19; 38}.
b) Ta có: 75 = 3.52
Tập hợp các ước của 75 là: {1; 3; 5; 15; 25; 75}.
c) 100 = 2.2.5.5 = 22.52.
Tập hợp các ước của 100 là: {1; 2; 4; 5; 10; 20; 25; 50; 100}.
Lời giải:
Nếu đựng trứng bằng khay Hình 1:
Quan sát Hình 1, dễ thấy: Khay có 3 hàng, mỗi hàng có 6 quả trứng.
Do đó mỗi khay ở Hình 1 đựng được số trứng là: 3.6 = 18 (quả)
Cần số khay để đựng 360 quả trứng là: 360 : 18 = 20 (khay).
Nếu đựng trứng bằng khay Hình 2:
Quan sát hình 2, dễ thấy: Khay có 5 hàng, mỗi hàng có 6 quả trứng.
Do đó mỗi khay ở Hình 2 đựng được số trứng là: 5.6 = 30 (quả)
Cần số khay để đựng 360 quả trứng là: 360 : 30 = 12 (khay).
Vậy nếu đựng trứng bằng khay Hình 1 thì cần dùng 20 khay, nếu đựng trứng bằng khay Hình 2 thì cần dùng 12 khay.
Lời giải:
Trường hợp 1: p chẵn
Do p là số nguyên tố nên p = 2, suy ra p + 1 = 3 và p + 5 = 7 đều là các số nguyên tố.
Vậy p = 2 thỏa mãn.
Trường hợp 2: p lẻ, do p là số nguyên tố nên p > 2
Khi đó p + 1 và p + 5 đều là các số chẵn lớn hơn 2, vì vậy p + 1 và p + 5 là hợp số.
Vậy với p = 2 thì p + 1 và p + 5 đều là số nguyên tố.
Bài 10 trang 29 sách bài tập Toán lớp 6 Tập 1: a) Tìm số tự nhiên k để 3.k là số nguyên tố.
b) Tìm số tự nhiên k để 7.k là số nguyên tố.
Lời giải:
a)
Nếu k = 0 thì 3k = 0, không là số nguyên tố
Nếu k = 1 thì 3k = 3 là một số nguyên tố
Nếu k >1, ta có 3.k chia hết cho 3 và k, do đó nó có ít nhất 3 ước là 1; 3; 3.k nên không là số nguyên tố.
Vậy k = 1 thì 3k là số nguyên tố.
b)
Nếu k = 0 thì 7k = 0, không là số nguyên tố
Nếu k = 1 thì 7k = 7 là một số nguyên tố
Nếu k > 1, ta có 7.k chia hết cho 7 và k, do đó nó có ít nhất 3 ước là 1; 7; 7.k nên không là số nguyên tố.
Vậy k = 1 thì 7k là số nguyên tố.
Lý thuyết Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
1. Số nguyên tố. Hợp số
− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
− Hợp số là số tự nhiên lớn hơn 1 có nhiều hơn hai ước.
Ví dụ:
+ Số 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.
+ Số 15 có bốn ước là 1; 3; 5; 15 nên 15 là hợp số.
Lưu ý: Số 0 và số 1 không là số nguyên tố cũng không là hợp số.
2. Phân tích một số ra thừa số nguyên tố
a. Thế nào là phân tích một số ra thừa số nguyên tố?
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Chú ý:
− Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
− Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
− Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.
Ví dụ:
- Số 5 là số nguyên tố và dạng phân tích ra thừa số nguyên tố của nó là 5.
- Số 18 là hợp số và 18 được phân tích ra thừa số nguyên tố là:
18 = 2 . 3 . 3 (hoặc viết gọn là 18 = 2 . 32).
b. Cách phân tích một số ra thừa số nguyên tố
Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc.
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Ví dụ: Số 76 được phân tích ra thừa số nguyên tố theo cột dọc như sau:
|
76 |
2 |
|
38 |
2 |
|
19 |
19 |
|
1 |
Vậy 76 = 22 . 19.
Chú ý: Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.
Cách 2: Phân tích một số ra thừa số nguyên tố theo sơ đồ cây.
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
Ví dụ: Số 36 được phân tích ra thừa số nguyên tố theo sơ đồ cây như sau:
Vậy 36 = 32 . 22.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
