Với giải sách bài tập Toán 6 Bài 9: Ước và bội sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 9: Ước và bội

Bài 1 trang 25 sách bài tập Toán lớp 6 Tập 1: Điền “ước” hoặc “bội” vào chỗ chấm cho thích hợp:

a) 35 là …… của 7

b) 72 là …… của 12

c) 9 là …… của 63

d) Cho a, b, c là các số tự nhiên khác 0. Nếu a = bc thì:

i. a là …… của b

ii. a là …… của c

iii. b là …… của a

iv. c là …… của a

Lời giải:

a) Vì 35 = 5.7 nên 35 chia hết cho 7 nên 35 là bội của 7. 

Ta điền: 35 là bội của 7

b) Vì 72 = 12.6 nên 72 chia hết cho 12 nên 72 là bội của 12.

Ta điền: 72 là bội của 12

c) Vì 63 = 9.7 nên 63 chia hết cho 9 hay 9 là ước của 63.

Ta điền: 9 là ước của 63

d) Vì a = bc nên a chia hết cho b, a chia hết cho c, khi đó:

a là bội của b hay b là ước của a

a là bội của c hay c là ước của a

Ta điền: 

i. a là bội của b

ii. a là bội của c

iii. b là ước của a

iv. c là ước của a

Bài 2 trang 25 sách bài tập Toán lớp 6 Tập 1: Viết lại mỗi tập hợp sau theo cách liệt kê các phần tử:

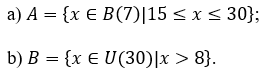
Lời giải:

a) Ta lấy 7 nhân lần lượt với các số tự nhiên 0; 1; 2; 3; 4; 5 … nên ta có: B(7) = {0; 7; 14; 21; 28; 35; …}.

Các số là bội của 7 và thỏa mãn lớn hơn hoặc bằng 15 và nhỏ hơn hoặc bằng 30 là: 21; 28.

Tập hợp A là tập hợp các bội của 7 thỏa mãn lớn hơn hoặc bằng 15 hoặc nhỏ hơn hoặc bằng 30. Khi đó, ta có: A = {21; 28}. 

Vậy A = {21; 28}.

b) Ta lấy 30 chia lần lượt cho các số tự nhiên từ 0 đến 30, ta thấy 30 chia hết cho 1; 2; 3; 5; 6; 10; 15; 30. 

⇒Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.

Các số là ước của 30 và thỏa mãn lớn hơn 8 là: 10; 15; 30.

Tập hợp B là tập hợp các ước của 30 thỏa mãn lớn hơn 18. Khi đó, ta có: B = {10; 15; 30}. 

Vậy B = {10; 15; 30}. 

Bài 3 trang 25 sách bài tập Toán lớp 6 Tập 1: a) Tìm các số tự nhiên a sao cho a là bội của 12 và 9 < a < 100.

b) Tìm các số tự nhiên b sao cho b là ước của 72 và 15<b≤36.

c) Tìm các số tự nhiên c sao cho c vừa là bội của 12 vừa là ước của 72 và 16≤c≤50.

Lời giải:

a) Ta lấy 12 nhân lần lượt với các số tự nhiên 0; 1; 2; 3; 4; 5; …. Ta được: B(12) = {0; 12; 24; 36; 48; 60; 72; 84; 96; 108; …}.

Ta có a là bội của 12 nên a∈ B(12) mà 9 < a < 100 suy ra a ∈{12; 24; 36; 48; 60; 72; 84; 96}.

Vậy a ∈ {12; 24; 36; 48; 60; 72; 84; 96}.

b) Ta lấy 72 chia có các số tự nhiên từ 1 đến chính nó, ta thấy 72 chia hết cho các số: 1; 2; 4; 6; 8; 9; 12; 18; 36; 72.

Ư(72) = {1; 2; 4; 6; 8; 9; 12; 18; 24; 36; 72}.

Vì b là ước của 72 nên b∈ Ư(72) và 15<b≤36 suy ra b ∈ {18; 24; 36}.

Vậy b ∈ {18; 24; 36}.

c) Vì c vừa là bội của 12 vừa là ước của 72 nên:

c∈ B(12) = {0; 12; 24; 36; 48; 60; 72; 84; 96; 108; …}.

Và c∈ Ư(72) = {1; 2; 4; 6; 8; 9; 12; 18; 24; 36; 72}.

Hơn nữa 16≤c≤50 nên c∈ {24; 36}.

Vậy c∈ {24; 36}.

Bài 4 trang 25 sách bài tập Toán lớp 6 Tập 1: Lớp của Lan có 36 bạn và phân công 2 bạn trực nhật một ngày. Hôm nay thứ Hai là ngày đầu tiên mà Lan và Mai trực nhật.

a) Lần trực nhật thứ ba của Lan và Mai cách lần trực nhật đầu tiên bao nhiêu ngày (không tính ngày được nghỉ học)

b) Trường Lan học 6 ngày mỗi tuần. Vậy lần trực thứ hai của Lan và Mai là vào ngày thứ mấy trong tuần? Biết rằng trong học kì 1, trường Lan không được nghỉ học ngày nào trừ các ngày chủ nhật.

Lời giải:

a) Số nhóm trực nhật của cả lớp là: 36 : 2 = 18 (nhóm)

Do không tính ngày nghỉ học và mỗi nhóm trực nhật một ngày nên số nhóm trực nhật cũng là số ngày trực nhật mỗi lượt của cả lớp.

Như vậy 2 lần trực liên tiếp của một nhóm sẽ cách nhau 18 ngày (không tính ngày nghỉ)

Hay lần thứ hai mà Lan và Mai trực nhật là sau 18 ngày (không tính ngày nghỉ)

Lần thứ ba mà Lan và Mai trực nhật là sau:18 + 18 = 36 (ngày) (không tính ngày nghỉ)

Vậy lần trực nhật thứ ba của Lan và Mai cách lần trực nhật đầu tiên 36 ngày (không tính ngày được nghỉ học)

b) Vì lần thứ hai mà Lan và Mai trực nhật là sau 18 ngày (không tính ngày được nghỉ học), tương ứng với 18 nhóm trực vào các ngày đi học.

Mỗi tuần có 6 ngày đi học, nên 18 ngày đi học tương ứng với: 18 : 6 = 3 (tuần)

Vậy sau 3 tuần Lan và Mai sẽ trực lần thứ hai, tức là vào ngày thứ Hai trong tuần.

Lý thuyết Ước và bội

1. Ước và bội

Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.

Ví dụ: Ta có 12 ⋮ 6.

Khi đó, 12 là bội của 6, còn 6 là ước của 12.

Tập hợp các ước của a được kí hiệu là Ư(a). Tập hợp các bội của a được kí hiệu là B(a).

Ví dụ: Ư(8) = {1; 2; 4; 8}; B(5) = {0; 5; 10; 15; 20; …}.

Chú ý:

- Số 0 là bội của tất cả các số tự nhiên khác 0. Số 0 không là ước của bất kì số tự nhiên nào.

- Số 1 chỉ có một ước là 1. Số 1 là ước của mọi số tự nhiên.

- Mọi số tự nhiên a lớn hơn 1 luôn có ít nhất hai ước là 1 và chính nó.

2. Cách tìm ước

Cách tìm Ư(a):

Ta có thể tìm các ước của a (a > 1), ta có thể lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.

Ví dụ:

Ta có 16 : 1 = 16; 16 : 2 = 8; 16 : 4 = 4; 16 : 8 = 2; 16 : 16 = 1.

Do đó các ước của 16 là: 1; 2; 4; 8; 16.

Vậy tập hợp các ước của 16 là: Ư(16) = {1; 2; 4; 8; 16}.

3. Cách tìm bội

Cách tìm B(a):

Muốn tìm bội của số tự nhiên a khác 0, ta có thể nhân a lần lượt với 0, 1, 2, 3, ...

Chú ý:

Bội của a có dạng tổng quát là a . k với k $\in \mathrm{\mathbb{N}}$. Ta có thể viết:

$B\left(a\right)=\{a.k|k\in \mathbb{N}\}$.

Ví dụ:

Ta có: 6 . 0 =0; 6 . 1 = 6; 6 . 2 = 12; 6 . 3 = 18; …

Do đó các bội của 6 là: 0; 6; 12; 18; …

Vậy B(6) = {0; 6; 12; 18; ...}