Với giải sách bài tập Toán 6 Bài 8: Dấu hiệu chia hết cho 3 và cho 9 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 3 và cho 9

Bài 1 trang 22 sách bài tập Toán lớp 6 Tập 1: Trong những số từ 1000 đến 1010, số nào

a) chia hết cho 3.

b) chia hết cho 9.

c) chia hết cho 3 nhưng không chia hết cho 9.

Lời giải:

Những số từ 1 000 đến 1 010 gồm các số: 1 000; 1 001; 1 002; 1 003; 1 004; 1 005; 1 006; 1 007; 1 008; 1 009; 1 010.

- Ta có: 1 + 0 + 0 + 0 = 1 không chia hết cho 3 và không chia hết cho 9 nên 1 000 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 1 = 2 không chia hết cho 3 và không chia hết cho 9 nên 1 001 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 2 = 3 chia hết cho 3 nhưng không chia hết cho 9 nên 1 002 chia hết cho 3 nhưng không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 3 = 4 không chia hết cho 3 và không chia hết cho 9 nên 1 003 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 4 = 5 không chia hết cho 3 và không chia hết cho 9 nên 1 004 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 5 = 6 chia hết cho 3 nhưng không chia hết cho 9 nên 1 005 chia hết cho 3 nhưng không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 6 = 7 không chia hết cho 3 và không chia hết cho 9 nên 1 006 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 7 = 7 không chia hết cho 3 và không chia hết cho 9 nên 1 007 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 0 + 8 = 9 chia hết cho 3 và chia hết cho 9 nên 1 008 chia hết cho 3 và chia hết cho 9.

- Ta có: 1 + 0 + 0 + 9 = 10 không chia hết cho 3 và không chia hết cho 9 nên 1 009 không chia hết cho 3 và không chia hết cho 9.

- Ta có: 1 + 0 + 1 + 0 = 2 không chia hết cho 3 và không chia hết cho 9 nên 1 010 không chia hết cho 3 và không chia hết cho 9.

a) Các số chia hết cho 3: 1 002; 1 005; 1 008.

b) Các số chia hết cho 9: 1 008

c) Các số chia hết cho 3 nhưng không chia hết cho 9 là: 1 002; 1 005.

Bài 2 trang 22 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số thích hợp thay cho dấu * để số  thỏa mãn điều kiện:

a) chia hết cho 3.

b) chia hết cho 9.

c) chia hết cho 3 nhưng không chia hết cho 9.

Lời giải:

Ta có: 5 + 4 + 3 + 2 + * = 14 + *

a) Để số 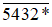 chia hết cho 3 thì 14 + * phải chia hết cho 3.

Mà * là chữ số nên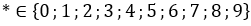 

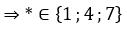
Vậy 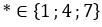 thì số  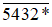chia hết cho 3.

b) Để số 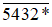  chia hết cho 9 thì 14 + * phải chia hết cho 9.

Mà * là chữ số nên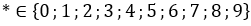 

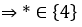
Vậy *= 4 thì số 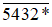 chia hết cho 9.

c) Để số 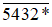   chia hết cho 3 mà không chia hết cho 9 thì .

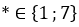Vậy với 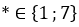 thì số  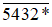chia hết cho 3 mà không chia hết cho 9.

Bài 3 trang 23 sách bài tập Toán lớp 6 Tập 1: Các kết quả sau đây chỉ có 1 kết quả sai, có thể thấy ngay là kết quả nào. Vì sao?

a) 12345679 . 9 = 111 111 111

b) 12345679 . 18 = 222 222 222

c) 12345679 . 27 = 333 333 333

d) 12345679 . 81 = 899 999 999

Lời giải:

Ý d) là đáp án sai, vì:

Ta có: 12345679 . 81 =  12345679 . 9 . 9  chia hết cho 9 (1)

Ta lại có 8 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 9.8 + 8;

Vì 9.8 chia hết cho 9 nhưng 8 không chia hết cho 9 nên 9.8 + 8 không chia hết cho 9.

Do đó 899 999 999 không chia hết cho 9 (2)

Từ (1) và (2) suy ra đáp án d) sai.

Bài 4 trang 23 sách bài tập Toán lớp 6 Tập 1: Có thể xếp đội quân gồm 13579 người thành đội hình chữ nhật mỗi hàng 9 người được không?

Lời giải:

Xếp đội quân gồm 13579 thành hình chữ nhật mỗi hàng 9 người nghĩa là xét xem 13 579 có chia hết cho 9 hay không?

Ta có: 1 + 3 + 5 + 7 + 9 = 25 không chia hết cho 9 nên 13 579 không chia hết cho 9.

Vì vậy không thể xếp đội quân gồm 13579 người thành đội hình chữ nhật mỗi hàng 9 người.

Lý thuyết Dấu hiệu chia hết cho 3, cho 9

1. Dấu hiệu chia hết cho 9

Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.

Ví dụ:

a) Số 1 944 chia hết cho 9 vì có tổng các chữ số là 1 + 9 + 4 + 4 = 18 chia hết cho 9.

b) Số 7 325 không chia hết cho 9 vì có tổng các chữ số là 7 + 3 + 2 + 5 = 17 không chia hết cho 9.

2. Dấu hiệu chia hết cho 3

Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.

Ví dụ:

a) Số 90 156 chia hết cho 3 vì có tổng các chữ số là 9 + 0 + 1 + 5 + 6 = 21 chia hết cho 3.

b) Số 6 116 không chia hết cho 3 vì có tổng các chữ số là 6 + 1 + 1 + 6 = 14 không chia hết cho 3.