Với giải sách bài tập Toán 6 Bài 4: Lũy thừa với số mũ tự nhiên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 4: Lũy thừa với số mũ tự nhiên

Bài 1 trang 14 sách bài tập Toán lớp 6 Tập 1: Các số 4; 8; 9; 16; 27; 64; 81; 125; 225 là bình phương hay lập phương của những số nào?

Lời giải:

Ta có: 4 = 2 . 2 = 2² ; 8 = 2 . 4 = 2 . 2² = 2³ ;  9 = 3 . 3 = 3² ;  

16 = 4 . 4 = 4² ;  27 = 3 . 9 = 3 . 3² = 3³ ;  

64 = 8 . 8 = 8² ; 64 = 4 . 16 = 4 . 4² = 4³ ;  81 = 9 . 9 = 9² 

125 = 5 . 25 = 5 . 5² = 5³ ;  225 = 3 . 75 = 3 . 5 . 15 = 15 . 15 = 15²

Do đó 4 = 2² ; 8 = 2³; 9 = 3² ; 16 = 4²  ; 27 = 3³ ; 64 = 8² = 4³ ; 81 = 9² ; 125 = 5³ ; 225 = 15²

Vậy các số 4; 9; 16; 64; 81; 225 là bình phương của lần lượt các số 2; 3; 4; 8; 9; 15

Các số 8; 27; 64; 125 là lập phương của lần lượt các số 2; 3; 4; 5.

Bài 2 trang 14 sách bài tập Toán lớp 6 Tập 1: Tính:

a) 2 . 10³ + 7 . 10² + 8 . 10 + 7;

b) 19 . 10³ + 5 . 10² + 6 . 10.

Lời giải:

a) 2 . 10³ + 7 . 10² + 8 . 10 + 7 

= 2 . 1 000 + 7 . 100 + 8 . 10 + 7

= 2 000 + 700 + 80 + 7 = 2 787

b) 19 . 10³ + 5 . 10² + 6.10 = 19 . 1 000 + 5 . 100 + 6 . 10

= 19 000 + 500 + 60 = 19 560

Bài 3 trang 14 sách bài tập Toán lớp 6 Tập 1: Cho số tự nhiên gồm 4 chữ số  .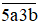

a) Viết cấu tạo thập phân của số này.

b) Tìm a và b sao cho số này là số lẻ và nhỏ hơn 5 033.

Lời giải:

a) Số 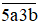gồm 5 nghìn, a trăm, 3 chục và b đơn vị. 

Cấu tạo thập phân: 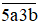 = 5 . 10³ + a . 10² + 3 . 10 + b

b) Số 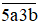nhỏ hơn 5 033 hay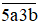 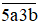 < 5 033

Chữ số hàng nghìn của hai số đều là 5, ta so sánh chữ số hàng trăm:

- Chữ số hàng trăm của  là a

- Chữ số hàng trăm của 5 033 là 0

Vì 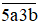 < 5 033 nên a = 0 và b < 3 hoặc a < 0, b tùy ý.

Mà 0 là số tự nhiên nhỏ nhất nên a = 0 và b < 3.

Ta có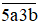 là số lẻ và có chữ số tận cùng là b nên b là số lẻ và b < 3 nên b = 1.

Vậy để 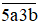là số lẻ và nhỏ hơn 5 033 thì a = 0, b = 1.

Bài 4 trang 14 sách bài tập Toán lớp 6 Tập 1: Ước tính có khoảng 100 tỉ nơ-ron thần kinh trong não người. Dù có số lượng rất lớn nhưng các nơ-ron thần kinh chỉ chiếm 10% tổng số tế bào não (nguồn VINMEC.com). Hãy viết các số chỉ nơ-ron thần kinh và số tế bào não trong não người (ước tính) dưới dạng lũy thừa của 10.

Lời giải:

Trong não người có khoảng 100 tỉ nơ-ron thần kinh hay 100 000 000 000 nơ-ron thần kinh.

Tức là có 10¹¹ nơ-ron thần kinh.

Số nơ-ron thần kinh chỉ chiếm 10% tổng số tế bào não

Nên số nơ-ron thần kinh = tổng số tế bào não × 10% tổng số tế bào não

Suy ra: Tổng số tế bào não = số nơ-ron thần kinh : 10%.

Số tế bào trong não người (ước tính) là: 10¹¹ : 10% = 10¹²

Vậy số nơ-ron thần kinh và số tế bào não trong não người (ước tính) lần lượt là 10¹¹ và 10¹².

Lý thuyết Lũy thừa với số mũ tự nhiên

1. Lũy thừa

Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.

aⁿ = a . a ….. a (n thừa số a) (n $\in \mathrm{\mathbb{N}}*$ )

Ta đọc aⁿ là “a mũ n” hoặc “lũy thừa bậc n của”.

Số a được gọi là cơ số, n được gọi là số mũ.

Ví dụ: 8⁵ đọc là “tám mũ năm”, có cơ số là 8 và số mũ là 5.

Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.

Đặc biệt, a² còn được đọc là “a bình phương” hay “bình phương của a”.

a³ được đọc là “a lập phương” hay “lập phương của a”.

Quy ước: a¹ = a.

Ví dụ:

a) Tính 2³ và 10³.

b) Viết 10 000 000 dưới dạng lũy thừa của 10.

c) Viết 16 dưới dạng lũy thừa cơ số 4

Hướng dẫn giải

a) Số 2³ là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:

2³ = 2 . 2 . 2 = 8.

Số 10³ là lũy thừa bậc 3 của 10 và là tích của 3 thừa số 10 nhân với nhau nên ta có:

10³ = 10 . 10 . 10 = 1 000.

b) Số 10 000 000 được viết dưới dạng lũy thừa của 10 là:

10 000 000 = 10 . 10 . 10 . 10 . 10 . 10 . 10 = 10⁷.

c) Số 16 được viết dưới dạng lũy thừa cơ số 4 là:

16 = 4 . 4 = 4².

2. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

a^m . aⁿ = a^{m + n}.

Ví dụ:

a) 3 . 3⁵ = 3¹ . 3⁵ = 3^{1 + 5} = 3⁶

b) 5² . 5⁴ = 5^{2 + 4} = 5⁶

c) a³ . a⁵ = a^{3 + 5} = a⁸.

3. Chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.

a^m : aⁿ = a^{m – n} (a ≠ 0; m ≥ n ≥ 0).

Quy ước: a⁰ = 1 (a ≠ 0).

Ví dụ:

a) a⁶ : a² = a^{6 − 2} = a⁴ (a ≠ 0)

b) 2³ : 2³ = 2^{3 − 3} = 2⁰ = 1

c) 81 : 3² = 3⁴ : 3² = 3^{4 − 2} = 3² = 3 . 3 = 9.