Với giải Bài 2 trang 97 Toán lớp 5 Kết nối tri thức chi tiết trong Bài 25: Hình tam giác. Diện tích hình tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 5. Mời các bạn đón xem:
Giải bài tập Toán lớp 5 Bài 25: Hình tam giác. Diện tích hình tam giác
Giải Toán lớp 5 trang 97 Bài 2: Vẽ các hình tam giác sau vào vở, sau đó vẽ đường cao ứng với đáy BC của mỗi hình tam giác đó.
Lời giải:
Tam giác KBC vuông tại B nên đường cao ứng với đáy BC chính là: BK
Lý thuyết Hình tam giác. Diện tích hình tam giác
1. Hình tam giác
a) Hình tam giác
|
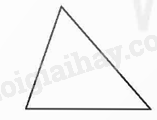
Hình tam giác có 3 góc nhọn gọi là hình tam giác nhọn. |
|
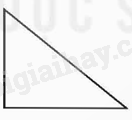
Hình tam giác có một góc vuông gọi là hình tam giác vuông. |
|
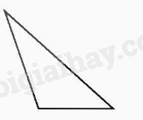
Hình tam giác có một góc tủ gọi là hình tam giác tù. |
|
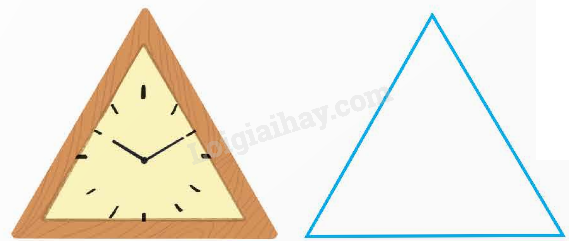
• Hình tam giác có 3 cạnh bằng nhau gọi là hình tam giác đều. • Hình tam giác đều có 3 góc bằng nhau và cùng bằng 60°. |
b) Đáy và đường cao của hình tam giác
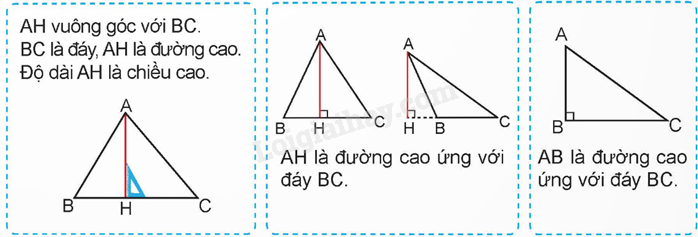
2. Vẽ đường cao của hình tam giác
a) Vẽ đường cao của hình tam giác có hai góc nhọn ở đáy.
|
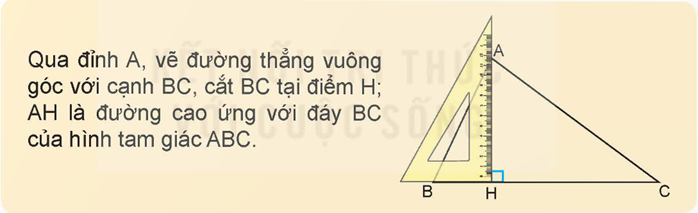
Muốn chia một số thập phân cho 10, 100, 1000,... ta chuyên dấu phẩy của số đó lần lượt sang bên trái một; hai; ba; … chữ số. |
b) Vẽ đường cao của hình tam giác có một góc tù ở đáy.
|
Muốn chia một số thập phân cho 0,1; 0,01; 0,001.... ta chuyến dâu phẩy của số đô lần lượt sang bên phải một, hai, ba, chữ số |
3. Diện tích hình tam giác
Cách tính diện tích hình tam giác:
|
Muốn tính diện tích hình tam giác ta0lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2. S = Trong đó: S là diện tích, a là độ dài đáy, h là chiều cao. |
Xem thêm lời giải bài tập Toán 5 Kết nối tri thức hay, chi tiết khác:
Giải Toán lớp 5 trang 92 Bài 1: Mỗi đồ vật dưới đây có dạng hình tam giác gì?...
Giải Toán lớp 5 trang 94 Bài 2: Vẽ hình (theo mẫu), biết rằng:...
Giải Toán lớp 5 trang 94 Bài 3: Em hãy vẽ một vì kèo vào vở...
Giải Toán lớp 5 trang 96 Bài 1: Tính diện tích của hình tam giác, biết:...
Giải Toán lớp 5 trang 96 Bài 2: Chọn câu trả lời đúng...
Xem thêm các bài giải bài tập Toán lớp 5 Kết nối tri thức hay, chi tiết khác:
Bài 25. Hình tam giác. Diện tích hình tam giác
Bài 26. Hình thang. Diện tích hình thang
Bài 27. Đường tròn. Chu vi và diện tích hình tròn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
