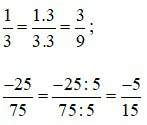Với giải sách bài tập Toán 6 Bài 23: Mở rộng phân số. Phân số bằng nhau sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 23: Mở rộng phân số. Phân số bằng nhau
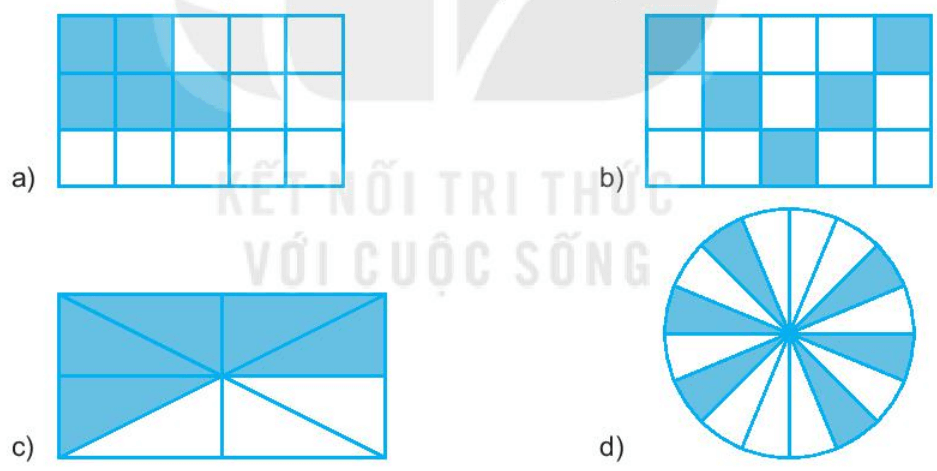
Lời giải:
- Hình a) là hình chữ nhật được chia thành 15 phần bằng nhau, tô màu 5 phần. Nên phân số biểu thị số phần tô màu là 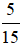 .
.
- Hình b) là hình chữ nhật được chia thành 15 phần bằng nhau, tô màu 5 phần. Nên phân số biểu thị số phần tô màu là 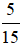 .
.
- Hình c) là hình chữ nhật được chia thành 8 phần bằng nhau, tô màu 5 phần. Nên phân số biểu thị số phần tô màu là 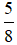 .
.
- Hình d) là hình chữ nhật được chia thành 16 phần bằng nhau, tô màu 6 phần. Nên phân số biểu thị số phần tô màu là 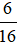 .
.
Bài 6.2 trang 5 sách bài tập Toán lớp 6 Tập 2: Viết các phép chia sau dưới dạng phân số.
a) (−17) : 8;
b) (−8) : (−9).
Lời giải:
Lời giải:
a) Phép chia (−17) : 8 viết dưới dạng phân số là 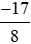 ;
;
b) Phép chia (−8) : (−9) viết dưới dạng phân số là 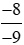 .
.
a) Mét: 15 cm; 40 mm;
b) Mét vuông: 15 cm2; 35 dm2.
Lời giải:
a) Các đơn vị đo độ dài sắp xếp theo thứ tự từ lớn đến bé lần lượt là: km, hm, dam, m, dm, cm, mm. Mỗi đơn vị đo độ dài đều gấp 10 lần đơn vị bé hơn, liền nó.
Ta có: 1 m = 100 cm, 1 m = 1 000 mm.
Khi đổi từ cm sang m, ta chia số đó cho 100 (viết dưới dạng phân số)
Khi đổi từ mm sang m, ta chia số đó cho 1 000 (viết dưới dạng phân số).
Phân số tối giản với đơn vị mét là:
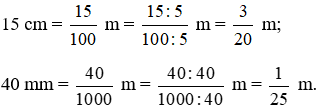
Vậy phân số để viết 15 cm; 40 mm theo mét lần lượt là 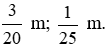
b) Các đơn vị đo diện tích sắp xếp theo thứ tự từ lớn đến bé lần lượt là: km2, hm2, dam2, m2, dm2, cm2, mm2. Mỗi đơn vị đo diện tích đều gấp 100 lần đơn vị bé hơn, liền nó.
Ta có: 1 m = 10 000 cm2, 1 m = 100 dm2.
Khi đổi từ cm2 sang m2, ta chia số đó cho 10 000 (viết dưới dạng phân số)
Khi đổi từ mm2 sang m2, ta chia số đó cho 1 000 000 (viết dưới dạng phân số).
Phân số tối giản với đơn vị mét vuông là:
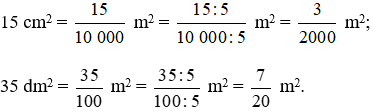
Vậy phân số để viết 15 cm2; 35 dm2 theo mét vuông lần lượt là 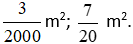
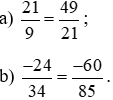
Lời giải:
Sử dụng tính chất: Chia cả tử và mẫu của phân số cho một ước chung của chúng, ta được một phân số mới bằng phân số đã cho.
a)
* Chia cả tử và mẫu của phân số 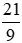 cho 3, ta được:
cho 3, ta được:
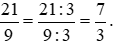
* Chia cả tử và mẫu của phân số 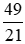 cho 7, ta được:
cho 7, ta được:

b)
* Chia cả tử và mẫu của phân số 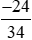 cho 2, ta được:
cho 2, ta được:
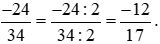
* Chia cả tử và mẫu của phân số 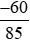 cho 5, ta được:
cho 5, ta được:
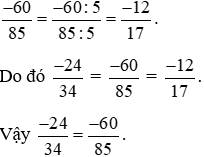
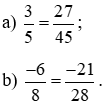
Lời giải:
Quy tắc bằng nhau của phân số: Hai phân số 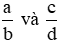 được gọi là bằng nhau, viết là
được gọi là bằng nhau, viết là 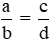 = nếu a . d = b . c.
= nếu a . d = b . c.
a) Ta có: 3 . 45 = 125 và 5 . 27 = 125
Nên 3 . 45 = 5 . 27 = 125.
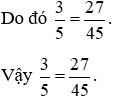
b) Ta có: (−6) . 28 = −168 và 8 . (−21) = −168
Nên (−6) . 28 = 8 . (−21) = −168.
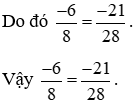
Bài 6.6 trang 6 sách bài tập Toán lớp 6 Tập 2: Tìm các số nguyên x, y thỏa mãn:
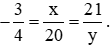
Lời giải:
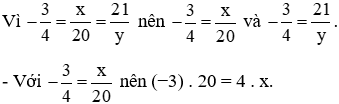
Suy ra 4 . x = −60.
Do đó x = −60 : 4= −15
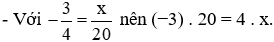
Suy ra (−3) . y = 84.
Do đó y = 84 : (−3) = −28.
Vậy x = −15, y = −28.
Bài 6.7 trang 6 sách bài tập Toán lớp 6 Tập 2: Rút gọn các phân số sau:
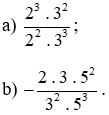
Lời giải:
Ta phân tích tử số và mẫu số thành tích các thừa số. Các thừa số giống nhau ở tử và mẫu có thể triệt tiêu cho nhau.
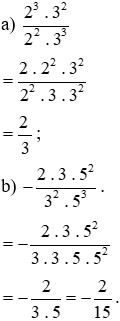
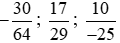
Lời giải:
Phân số có ước chung lớn nhất của tử và mẫu số bằng 1 thì gọi phân số tối giản.
- Phân số 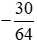 có tử số là 30 và mẫu số là 64 đều là các số chẵn.
có tử số là 30 và mẫu số là 64 đều là các số chẵn.
Nên hai số này chia hết cho 2.
Do đó, phân số 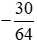 chưa là phân số tối giản.
chưa là phân số tối giản.
Rút gọn: 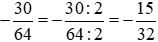
- Phân số 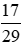 có tử số là 17 và mẫu số là 29.
có tử số là 17 và mẫu số là 29.
Mà ƯCLN (17, 29) = 1.
Do đó 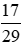 là phân số tối giản.
là phân số tối giản.
- Phân số 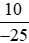 có tử số là 10 và mẫu số là −25 đều chia hết cho 5.
có tử số là 10 và mẫu số là −25 đều chia hết cho 5.
Do đó, phân số 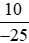 chưa là phân số tối giản.
chưa là phân số tối giản.
Rút gọn: 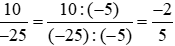 .
.
Em hãy viết phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E), rồi rút gọn về phân số tối giản.

Lời giải:
Tần số nốt Đô (C) là 264;
Tần số nốt Mi (E) là 330.
Phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E) là:
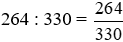
Rút gọn về phân số tối giản:
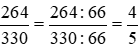
Vậy phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E) là 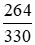 , rút gọn về phân số tối giản là
, rút gọn về phân số tối giản là 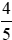 .
.
(Ngoài ra, ta có thể rút gọn từng bước lần lượt như sau:
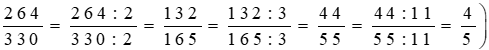
Lời giải:
Rút gọn phân số rồi nhân cả tử và mẫu của phân số với cùng một số sao cho cả tử và mẫu thu được là các số tự nhiên có hai chữ số.
Rút gọn: 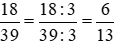
Số lớn nhất có hai chữ số là 99.
Ta có 99 : 13 = 7 dư 8.
(Nếu tử số > mẫu số thì thực hiện phép chia 99 cho tử số, ngược lại nếu tử số < mẫu số thì thực hiện phép chia 99 cho mẫu số).
Phân số 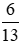 có tử số là số tự nhiên có một chữ số.
có tử số là số tự nhiên có một chữ số.
Ta nhân phân số 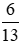 lần lượt với các số 2; 3;…; 7, ta được:
lần lượt với các số 2; 3;…; 7, ta được:
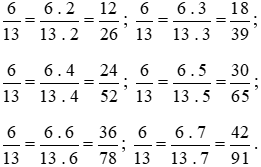
Vậy các phân số bằng phân số 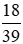 mà có tử và mẫu số là các số tự nhiên có hai chữ số là
mà có tử và mẫu số là các số tự nhiên có hai chữ số là 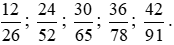
Lý thuyết Mở rộng phân số. Phân số bằng nhau
1. Mở rộng khái niệm về phân số
– Định nghĩa về phân số: Với a, b ∈ ℤ, b ≠ 0 , ta gọi 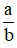 là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
Ví dụ 1:
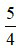 là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
 là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
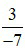 là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.
Ví dụ 2:
Số 3 có thể viết dưới dạng phân số là 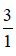 .
.
Số –8 có thể viết dưới dạng phân số là 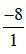 .
.
2. Hai phân số bằng nhau
Hai phân số  và
và 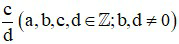 được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là
được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là 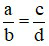 .
.
Ví dụ 3: Hai phân số 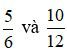 bằng nhau vì 5.12 = 60 và 6.10 = 60.
bằng nhau vì 5.12 = 60 và 6.10 = 60.
3. Tính chất cơ bản của phân số
– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
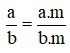 với a, b, m ∈ ℤ; b≠0; m≠0.
với a, b, m ∈ ℤ; b≠0; m≠0.
– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
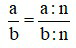 với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
Ví dụ 4: