Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 11 Bài 4: Phương trình lượng giác cơ bản sách Cánh diều. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 11.
Trắc nghiệm Toán 11 Bài 4: Phương trình lượng giác cơ bản
Câu 1. Giải phương trình .
A. .
B. .
C. .
D. .
Đáp án đúng là: C
Câu 2. Phương trình lượng giác có nghiệm là:
A. .
B. .
C. .
D. Vô nghiệm.
Đáp án đúng là: B
Ta có
Câu 3. Phương trình lượng giác có nghiệm là
A. .
B. .
C. .
D. .
Đáp án đúng là: B
Câu 4. Giải phương trình lượng giác có nghiệm là:
A. .
B. .
C. .
D. .
Đáp án đúng là: D
Câu 5. Tìm tất cả các giá trị thực của tham số m để phương trình vô nghiệm.
A. .
B. .
C. .
D. .
Đáp án đúng là: A
Áp dụng điều kiện có nghiệm của phương trình .
-Phương trình có nghiệm khi .
-Phương trình vô nghiệm khi .
Phương trình .
Do đó, phương trình vô nghiệm .
Câu 6. Nghiệm của phương trình là
A. .
B. .
C. .
D. .
Đáp án đúng là: B
Ta có:
Câu 7. Tìm tất cả các giá trị thực của tham số m để phương trình x = m có nghiệm.
A.
B.
C. .
D.
Đáp án đúng là: C
Với mọi , ta luôn có .
Do đó, phương trình có nghiệm khi và chỉ khi
Câu 8. Nghiệm của phương trình là:
A. .
B. .
C. .
D. .
Đáp án đúng là: C
Câu 9. Tập nghiệm của phương trình là
A. .
B. .
C. .
D. .
Đáp án đúng là: B
Ta có
Câu 10. Phương trình có nghiệm là
A. .
B. .
C. .
D. .
Đáp án đúng là: A
Câu 11. Số nghiệm của phương trình trên đoạn là:
A. 4.
B. 1.
C. 2.
D. 3.
Đáp án đúng là: C
Đặt . Khi đó ta có phương trình .
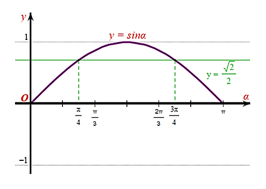
Xét đường thẳng và đồ thị hàm số trên đoạn :
Từ đồ thị hàm số trên ta thấy đường thẳng cắt đồ thị số trên đoạn tại hai điểm có hoành độ lần lượt là và .
Mà , khi đó ta sẽ tìm được 2 giá trị x là và .
Câu 12. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm ?
A. 2.
B. 1.
C. 0.
D. 3.
Đáp án đúng là: A
Ta có:
Đặt , điều kiện
PT trở thành
YCBT có nghiệm thuộc .
Số nghiệm của PT (1) là số giao điểm của parabol và đường thẳng (song song hoặc trùng Ox)
Bảng biến thiên
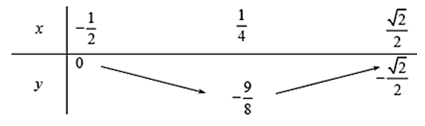
Dựa vào bảng biến thiên . Vì nên .