20 câu Trắc nghiệm Hàm số lượng giác (Kết nối tri thức 2024) có đáp án

20 câu Trắc nghiệm Hàm số lượng giác (Kết nối tri thức 2024) có đáp án - Toán lớp 11

Admin Vietjack Ngày: 31-12-2023 Lớp 11

2.2 K

Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 11 Bài 3: Hàm số lượng giác sách Kết nối tri thức. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 11.

Trắc nghiệm Toán 11 Bài 3: Hàm số lượng giác

Câu 1. Tìm tập giá trị của hàm số y = 3cos2x + 5

A. T = [-1;1]. B. T = [-1;11] C. T = [2;8] D. T = [5;8]

Hướng dẫn giải

Đáp án đúng là: C

Ta có -1 $\leq$ cos2x $\leq$ 1 $\to$ -3 $\leq$ 3cos2x $\leq$ 3 $\to$ 2 $\leq$ 3cos2x+5 $\leq$ 8

$\to$ 2 $\leq$ y $\leq$ 8 $\to$ T = [2;8].

Câu 2. Hàm số y = 5+4sin2xcos2x có tất cả bao nhiêu giá trị nguyên?

A. 3. B. 4. C. 5. D. 6.

Hướng dẫn giải

Đáp án đúng là: C

Ta có y = 5+4sin2xcos2x = 5+2sin4x. .

Mà -1 $\leq$ sin4x $\leq$ 1 $\to$ -2 $\leq$ 2sin4x $\leq$ 2 $\to$ 3 $\leq$ 5+2sin4x $\leq$ 7

→ y $\leq$ 7 $\to 3 \leq y \leq 7 \overset{y \in ℤ}{\to} y \in$ {3;4;5;6;7} nên y có 5 giá trị nguyên.

Câu 3. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx + cosx. Tính P = M - m.

A. P = 4 B. P = 2 $\sqrt{2}$ C. P = $\sqrt{2}$ D. P = 2

Hướng dẫn giải

Đáp án đúng là: B

Ta có y = sinx + cosx = $\sqrt{2}$ sin $(x + \frac{π}{4})$ .

Mà -1 $\leq$ sin $(x + \frac{π}{4})$ $\leq$ 1 $\to$ - $\sqrt{2}$ $\leq$ $\sqrt{2}$ sin $(x + \frac{π}{4})$ $\leq$ $\sqrt{2}$

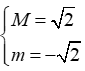
$\to$ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 $\to$ P = M - m = 2 $\sqrt{2}$ .

Câu 4. Tìm chu kì T của hàm số y = cos2x + sin $\frac{π}{2}$

A. T = 4 $π$ B. T = $π$ C. T = 2 $π$ D. T = $\frac{π}{2}$

Hướng dẫn giải

Đáp án đúng là: A

Hàm số y = cos2x tuần hoàn với chu kì $T_{1} = \frac{2 π}{2} = π .$

Hàm số y = sin $\frac{x}{2}$ tuần hoàn với chu kì $T_{2} = \frac{2 π}{\frac{1}{2}} = 4 π .$

Suy ra hàm số y = cos2x + sin $\frac{x}{2}$ tuần hoàn với chu kì T = 4 $π$ .

Nhận xét. T là của T₁ và T₂

Câu 5. Tìm chu kì T của hàm số y = cos3x + cos5x.

A. T = $π$ B. T = 3 $π$ C. T = 2 $π$ D. T = 5 $π$

Hướng dẫn giải

Đáp án đúng là: C

Hàm số y = cos3x tuần hoàn với chu kì $T_{1} = \frac{2 π}{3} .$

Hàm số Y = cos5x tuần hoàn với chu kì $T_{2} = \frac{2 π}{5} .$

Suy ra hàm số y = cos3x + cos5x tuần hoàn với chu kì T = 2 $π$

Câu 6. Tìm tập xác định D của hàm số $y = \frac{2021}{\sin x} .$

A. D = $ℝ$ B. D = $ℝ$ \{0}

C. D = $ℝ$ \{k $π$ , $\in$ $ℤ$ } D. D = $ℝ$ \

Hướng dẫn giải

Đáp án đúng là: C

Hàm số xác định khi và chỉ khi sinx $\neq$ 0 $\Leftrightarrow$ x $\neq$ k $π$ , k $\in$ $ℤ$ .

Vật tập xác định D = $ℝ$ \{k $π$ ,k $\in$ $ℤ$ }.

Câu 7. Trong các hàm số sau đây, hàm số nào không tuần hoàn?

A. y = cosx B. y = cos2x C. y = x²cosx. D. y = $\frac{1}{\sin 2 x}$

Hướng dẫn giải

Đáp án đúng là: C

Câu 8. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Hỏi hàm số đó là hàm số nào?

A. y = 1+sin2x B. y = cosx C. y = -sinx D. y = -cosx

Hướng dẫn giải

Đáp án đúng là: B

Ta thấy tại x = 0 thì y = 1. Do đó loại đáp án C và D.

Tại x = $\frac{π}{2}$ thì y = 0. Do đó chỉ có đáp án B thỏa mãn.

Câu 9. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 3sinx - 2

A. M = 1, m = -5. B. M = 3, m = 1 C. M = 2, m = -2 D. M = 0, m = -2.

Hướng dẫn giải

Đáp án đúng là: A

Ta có $- 1 \leq \sin x \leq 1 \to - 3 \leq 3 \sin x \leq 3 \to - 5 \leq 3 \sin x - 2 \leq 1$

$\to - 5 \leq y \leq 1 \to$ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Câu 10. Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y = sin2x B. y = xcosx C. y = cosx.cotx D. y = $\frac{\tan x}{\sin x}$

Hướng dẫn giải

- Xét hàm số y = f(x) = sin2x.

TXĐ: D = $ℝ$ . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có f(-x) = sin(-2x) = -sin2x = -f(x) $\to$ f(x) là hàm số lẻ.

-Xét hàm số y = f(x) = xcosx.

TXĐ: D = $ℝ$ . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có f-x) = (-x).cos(-x) = -xcosx = -f(x) $\to$ f(x) là hàm số lẻ.

-Xét hàm số y = f(x) = cosx.cotx.

TXĐ: D = $ℝ$ \{k $π$ (k $\in$ $ℤ$ )}. Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có f(-x) = cos(-x).cot(-x) = -cosxcotx = -f(x) $\to$ f(x) là hàm số lẻ.

- D = $ℝ$ .Xét hàm số y = f(x) = $\frac{\tan x}{\sin x}$ .

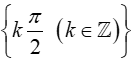
TXĐ: D = $ℝ$ \ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có $f (- x) = \frac{\tan (- x)}{\sin (- x)} = \frac{- \tan x}{- \sin x} = \frac{\tan x}{\sin x} = f (x)$ $\to f (x)$ là hàm số chẵn.

Câu 11. Hàm số nào sau đây có chu kì khác $π$ ?

A. $y = \sin (\frac{π}{3} - 2 x) .$ B. $y = \cos 2 (x + \frac{π}{4}) .$

C. y = tan(-2x+1). D. y = cosxsinx

Hướng dẫn giải

Đáp án đúng là: C

Vì y = tan(-2x+1) có chu kì 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Nhận xét. Hàm số y = cosxsinx = $\frac{1}{2}$ sin2x có chu kỳ là $π$ .

Câu 12. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

A. $y = \frac{1}{\sin^{3} x} .$ B. $y = \sin (x + \frac{π}{4}) .$

C. $y = \sqrt{2} \cos (x - \frac{π}{4}) .$ D. $y = \sqrt{\sin 2 x} .$

Hướng dẫn giải

Đáp án đúng là: A

Viết lại đáp án B là $y = \sin (x + \frac{π}{4}) = \frac{1}{\sqrt{2}} (\sin x + \cos x) .$

Viết lại đáp án C là $y = \sqrt{2} \cos (x - \frac{π}{4}) = \sin x + \cos x .$

Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.

Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ.

Xét đáp án D:

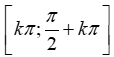
- Hàm số xác định $\Leftrightarrow$ sin2x $\geq$ 0 $\Leftrightarrow$ 2x $\in$ [k2 $π$ ; $π$ +k2 $π$ ] $\Leftrightarrow$ x $\in$ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11