Với lời giải Toán 11 trang 79 Tập 1 chi tiết trong Bài tập cuối chương 3 trang 79 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài tập cuối chương 3 trang 79
Bài 1 trang 79 Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x0 là:
A. ;
B. ;
C. ;
D. .
Lời giải:
Theo lí thuyết ta chọn đáp án D
Bài 2 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:
a) lim;
b) lim;
c) lim;
d) lim;
e) lim;
g) lim.
Lời giải:
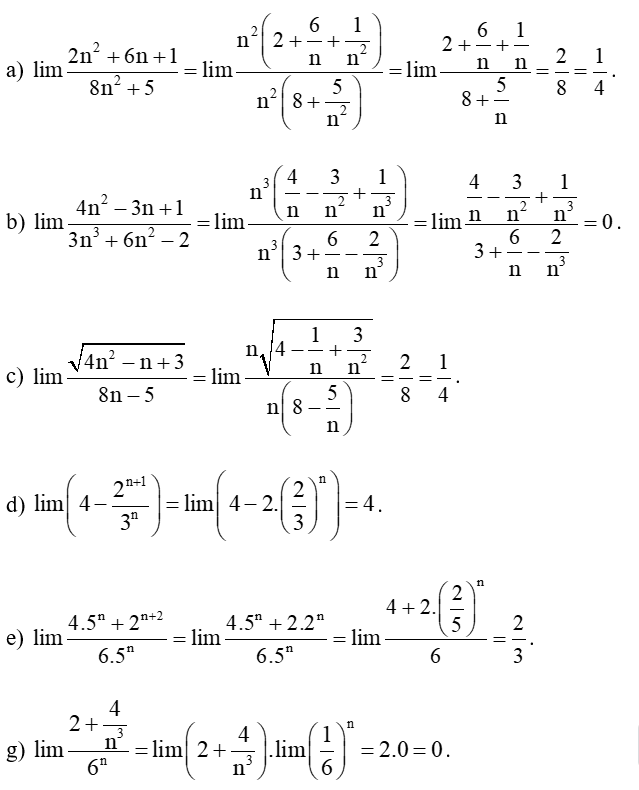
Bài 3 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:
a) ;
b) ;
c) .
Lời giải:
a) -5.(-3)+6 = -3.
b) .
c)
Bài 4 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:
a) ;
b) ;
c) ;
d) ;
e) ;
g) .
Lời giải:
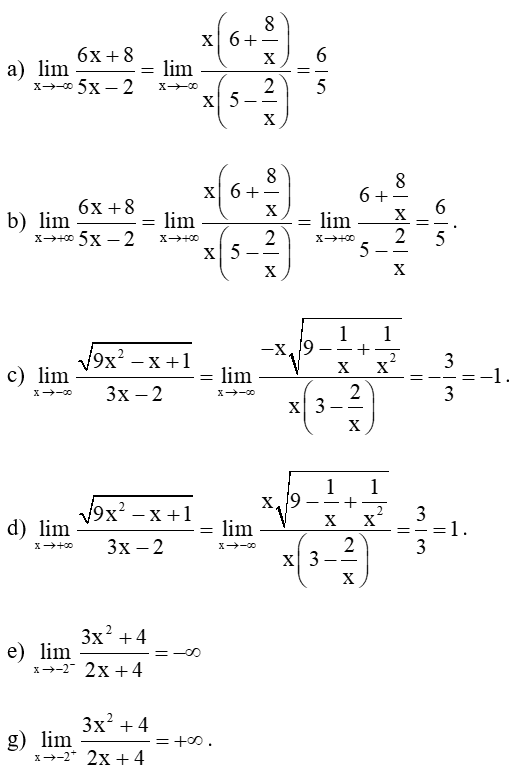
Bài 5 trang 79 Toán 11 Tập 1: Cho hàm số f(x) = 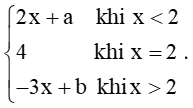
a) Với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2.
b) Với giá trị nào của a, b thì hàm số liên tục tại x = 2?
c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?
Lời giải:
a) Với a = 0, b = 1, hàm số f(x) = 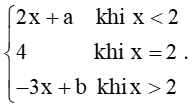
Với x < 2 thì f(x) = 2x là hàm liên tục.
Với x > 2 thì f(x) = – 3x + 1 là hàm liên tục.
Tại x = 2 ta có:
, .
Suy ra . Do đó không tồn tại .
Vậy hàm số tiên tục trên ( – ∞; 2) và (2; +∞).
b) Ta có:
,
Để hàm số liên tục tại x = 2 thì:
 .
.
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Để hàm số liên tục trên ℝ thì hàm số liên tục tại x = 2. Vì vậy với a = 0 và b = 10 thỏa mãn điều kiện.
Xem thêm các lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1 trang 79 Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x0 là:...
Bài 2 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 3 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 4 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:...
Bài 5 trang 79 Toán 11 Tập 1: Cho hàm số f(x) = 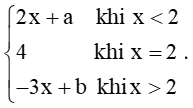 ...
...
Bài 6 trang 80 Toán 11 Tập 1: Từ độ cao 55,8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại này lên độ cao bằng độ cao mà quả bóng đạt được trước đó. Gọi Sn là tổng quãng đường di chuyển của quả bóng tính từ lúc thả vật bạn đầu cho đến khi quả bóng đó chạm đất n lần. Tính limSn....
Bài 7 trang 80 Toán 11 Tập 1: Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A2B2C2, ..., Tam giác An+1Bn+1Cn+1 có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, ... Gọi p1, p2, ..., pn, ... và S1, S2, ..., Sn, ... theo thứ tự là chu vi và diện tích của tam giác A1B1C1, A2B2C2, ..., AnBnCn, ...
Bài 8 trang 80 Toán 11 Tập 1: Một thấu kính hội tụ có tiêu cự là f. Gọi d và d’ lần lượt là khoảng cách từ một vật thật AB và từ ảnh A’B’ của nó tới quang tâm O của thấu kính như Hình 19. Công thức thấu kính ....
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 3: Hàm số liên tục
Bài tập cuối chương 3
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song