Tailieumoi sưu tầm và biên soạn chuyên đề Các dạng toán Hình học lớp 5 gồm đầy đủ lý thuyết và 18 bài tập chọn lọc từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, biết cách làm bài tập môn Toán lớp 5.

Chuyên đề Các dạng toán Hình học lớp 5

I/ Lý thuyết

Chuyên đề này sẽ giúp các em giải các bài toán có chứa yếu tố hình học trong đề bài.

II/ Các dạng bài tập

II.1/ Dạng 1: Các bài toán về các hình học phẳng

1. Phương pháp giải

Các bài toán về các hình học phẳng được chia ra làm 2 dạng nhỏ:

- Các bài toán không có nội dung thực tế: là các bài toán đề bài cho một hình vẽ, cho số liệu và yêu cầu tính diện tích, chu vi hoặc một cạnh nào đó...

- Các bài toán có chứa nội dung thực tế: Trong đề bài toán có những dữ liệu liên quan đến đời sống thực tế.

- Đối với dạng toán này chúng ta cần nhớ và áp dụng công thức tính chu vi, diện tích các hình học phẳng đã học: hình vuông, hình chữ nhật, hình tam giác, hình tròn, hình thang, hình bình hành..

2. Bài tập minh họa

Bài 1: Tính diện tích hình ngũ giác ABCDE có kích thước như hình vẽ.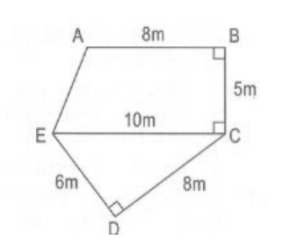

Hướng dẫn: Diện tích hình ngũ giác ABCDE bằng tổng diện tích hình thang ABCE và diện tích hình tam giác ECD.

Diện tích hình thang ABCE là: (8 + 10) x 5 : 2 = 45 (m² )

Diện tích hình tam giác ECD là: 6 x 8 : 2 = 24 (m² )

Diện tích hình ngũ giác ABCDE là: 45 + 24 = 69 (m² )

Đáp số: 69m²
Bài 2: Một thửa ruộng hình thang có đáy lớn 120m, đáy bé bằng $\frac{2}{3}$ đáy lớn. Đáy bé dài hơn chiều cao 5m. Trung bình cứ 100m²  thì thu hoạch được 72kg thóc. Tính số ki-lô-gam thóc thu được trên thửa ruộng đó.

Hướng dẫn:

+Áp dụng cách tính tìm phân số của một số để tìm đáy bé.

+Tìm chiều cao dựa vào độ dài đáy bé.

+Tính diện tích thửa ruộng hình thang.

+Tính số thóc thu hoạch được

Đáy bé dài số ki-lô-mét là: $120\times \frac{2}{3}=80$ (m)

Chiều cao là: 80 – 5 = 75 (m)

Diện tích thửa ruộng là:

(120 + 80) x 75 : 2 = 7500 (m² )

Thửa ruộng đó thu hoạch được số ki-lô-gam thóc là:

7500 : 100 x 72 = 5400 (kg)

Đáp số: 5400 kg thóc

II.2/ Dạng 2: Các bài toán về các hình khối

1. Phương pháp giải

- Dạng toán này bao gồm những bài tập liên quan đến hình lập phương, hình hộp chữ nhật

- Để giải được các dạng toán này, các em cần nắm rõ cách tính diện tích xung quanh, diện tích toàn phần và thể tích của các hình.

2. Bài tập minh họa

Bài 1: Tính thể tích khối gỗ như hình vẽ:

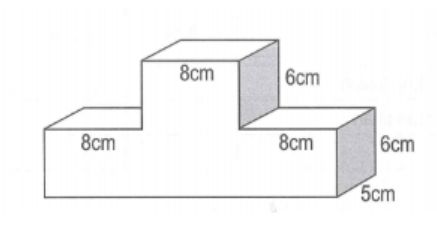
Hướng dẫn: Để tính thể tích của khối gỗ, chúng ta chia hình thành 2 hình hộp chữ nhật nhỏ. Tính thể tích của 2 hình hộp chữ nhật. Thể tích của khối gỗ bằng tổng thể tích của 2 hình nhỏ.

Thể tích của hình hộp chữ nhật nhỏ là:

8 x 5 x 6 = 240 (cm³ )

Thể tích của hình hộp chữ nhật lớn là:

(8 + 8 + 8)  x 5 x 6 = 720 (cm³ )

Thể tích của khối gỗ là: 240 + 720 = 960 (cm³ )

Đáp số: 960cm³

Bài 2: Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 2,5m, chiều rộng 1,8m và chiều cao 2m. Người thợ cần bao nhiêu ki-lô-gam sơn để đủ sơn mặt ngoài của thùng? Biết rằng mỗi ki-lô-gam sơn sơn được 5m² mặt thùng.

Hướng dẫn: Đầu tiên ta cần tính diện tích xung quanh, diện tích toàn phần của thùng đựng hàng. Sau đó tính khối lượng số sơn cần dùng.

Diện tích xung quanh thùng đựng hàng là:

(2,5 + 1,8) x 2 x 2 = 17,2 (m² )

Diện tích 2 đáy của thùng đựng hàng là:

2,5 x 1,8 x 2 = 9 (m² )

Diện tích toàn phần của thùng đựng hàng là:

17,2 + 9 = 26,2 (m² )

Khối lượng ki-lô-gam sơn cần dùng là:

26,2 : 5 = 5,24 (kg)

Đáp số: 5,24kg

III/ Bài tập vận dụng

1. Bài tập có lời giải

Bài 1: Cho tam giác ABC. Trên cạnh BC ta lấy 6 điểm. Nối đỉnh A với mỗi điểm vừa chọn. Hỏi đếm được bao nhiêu hình tam giác.

Lời giải:

    Ta nhận xét :

    - Khi lấy 1 điểm thì tạo thành 2 tam giác đơn ABD      và ADC. Số tam giác đếm được là 3 : ABC, ADB và     ADC. Ta có :   1 + 2 = 3 (tam giác)

    - Khi lấy 2 điểm thì tạo thành 3 tam giác đơn và số    tam giác đếm được là 6 : ABC, ABD, ADE, ABE,          ADC và AEC. Ta có : 1+ 2 + 3 = 6 (tam giác)

Vậy khi lấy 6 điểm ta sẽ có 7 tam giác đơn được tạo thành và số tam giác đếm được là : 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (tam giác)

Cách 2:

- Nối A với mỗi điểm D, E, …, C ta được một tam giác có cạnh AD. Có 6 điểm như vậy nên có 6 tam giác chung cạnh AD (không kể tam giác ADB vì đã tính rồi)

- Lập luận tương tự như  trên theo thứ tự ta có 5, 4, 3, 2, 1 tam giác chung cạnh AE, AP, …, AI.

- Vậy số tam giác tạo thành là : 7 + 6 + 5 + 4 +3 +2 + 1 = 28 (tam giác).

Bài 2: Cho hình chữ nhật ABCD. Chia mỗi cạnh AD và BC thành 4 phần bằng nhau, AB và CD thành 3 phần bằng nhau, rồi nối các điểm chia như hình vẽ.

Ta đếm được bao nhiêu hình chữ nhật trên hình vẽ?

    Lời giải:

     - Trước hết Ta xét các hình chữ nhật tạo bởi hai đoạn    AD, EP và các đoạn nối các điểm trên hai cạnh AD và      BC. Bằng cách tương tự như tronh ví dụ 1 ta tính được    10 hình.

- Tương tự ta tính được số hình chữ nhật tạo thành do hai đoạn EP và MN, do MN và BC đều bằng 10.

- Tiếp theo ta tính số hình chữ nhật tạo thành do hai đoạn AD và MN, EP và BC với các đoạn nối các điểm trên hai cạnh AD và BC đều bằng 10. 

Vì vậy :

Số hình chữ nhật đếm được trên hình vẽ là :10 + 10 + 10 + 10 + 10 + 10 = 60 (hình)

Đáp số 60 hình.

Bài 3: Cần ít nhất bao nhiêu điểm để khi nối lại ta được 5 hình tứ giác ?

Lời giải:

- Nếu ta chỉ có 4 điểm ( trong đó không có  3 điểm nào cùng nằm trên 1 đoạn thẳng) thì nối lại chỉ được 1 hình tứ giác.

 - Nếu ta chọn 5 điểm, chẳng hạn A, B, C, D, E (trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng) thì :

+ Nếu ta chọn A là 1 đỉnh thì khi  chọn thêm 3 trong số 4 điểm còn lại   B, C, D, E và nối lại ta sẽ được một tứ giác  có một đỉnh là A. Có 4 cách chọn 3 điểm trong số 4 điểm B, C, D, E để ghép với A. Vậy có 4 tứ giác đỉnh A.

- Có 1 tứ giác không nhận A làm đỉnh, dó là BCDE. Từ kết quả trên đây ta suy ra 

Khi có 5 điểm ta được 5 tứ giác.

Vậy để có 5 hình tứ giác ta cần ít nhất 5 điểm khác nhau (trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng)

Bài 4: Cho tam giác ABC có diện tích là 150 cm2. Nếu kéo dài đáy BC (về phía B) 5 cm thì diện tích sẽ tăng thêm 37,5 cm2 . Tính đáy BC của tam giác.

Lời giải:

Cách 1 : Từ A kẻ đường cao AH của ∆ ABC thì AH cũng là đường cao của ∆ ABD 

Đường cao AH là : 37,5 x 2 : 5 = 15 (cm)

Đáy BC là : 150 x 2 : 15 = 20 (cm)

Đáp số 20 cm.

Cách 2 : 

Từ A hạ đường cao AH vuông góc với BC . Đường cao AH là đường cao chung của hai tam giác ABC và ABD . Mà : Tỉ số 2 diện tích tam giác là :

Hai tam giác có tỉ số diện tích là 4 mà chúng có chung đường cao,nên tỉ số 2 đáy cũng là 4. Với đáy BC là : 5 x 4 = 20 (cm)

Đáp số 20 cm.

Bài 5: Cho tam giác ABC vuông ở A có cạnh AB dài 24 cm, cạnh AC dài 32 cm. Điểm M nằm trên cạnh AC. Từ M kẻ đường song song với cạnh AB cắt BC tại N. Đoạn MN dài 16 cm. Tính đoạn MA.

Lời giải:

Diện tích tam giác NCA là: 32 x 16 : 2 = 256 (cm2)

Diện tích tam giác ABC là :

24 x 32 : 2 = 348 (cm2)

384 – 256 = 128 (cm2)

Chiều cao NK hạ từ N xuống AB là : 128 x 2 : 24 = 10 ⅔ (cm)

Vì MN || AB nên tứ giác MNBA là hình thang vuông. Do vậy MA cũng bằng 10 ⅔cm

Đáp số: 10 ⅔ cm

Bài 6: Cho tam giác ABC vuông ở A. Cạnh AB dài 28 cm, cạnh AC dài 36 cm M là một điểm trên AC và cách A là 9 cm. Từ M kẻ đường song song với AB và đường này cắt cạnh BC tại N. Tính đoạn MN.

Lời giải:

Vì MN ||  AB nên MN ⊥ AC tại M. Tứ giác MNAB là hình

thang vuông. Nối NA. Từ N hạ NH⊥ AB thì NH là chiều cao của tam giác NBA và của hình thang MNBA nên NH = MA và là 9 cm.

Diện tích tam giác NBA là : 28 x 9 : 2 = 126 (cm2)

Diện tích tam giác ABC là : 36 x 28 : 2 = 504 (cm2)

Diện tích tam giác NAC là : 504 – 126 = 378 (cm2)

Đoạn MN dài là : 378 x 2 : 36 = 21 (cm)

2. Bài tập vận dụng

Bài 1: Một tấm bìa hình bình hành có chu vi 4dm. Chiều dài hơn chiều rộng 10cm và bằng  chiều cao. Tính diện tích tấm bìa đó.

Bài 2: Một hình vuông có diện tích bằng 4/9 diện tích của một hình bình hành có đáy 25cm và chiều cao 9cm. Tính cạnh của hình vuông.

Bài 3: Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m. Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.

Bài 4: Một viên gạch dạng hình hộp chữ nhật có chiều dài 22cm, chiều rộng 10cm, chiều cao 5,5 cm.Tính diện tích xung quanh và diện tích toàn phần của diện tích toàn phần của khối gạch dạng hình hộp chữ nhật do 6 viên gạch xếp thành.

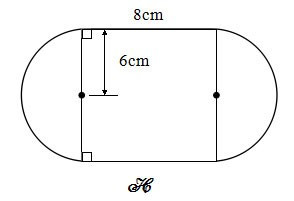
Bài 5: Diện tích hình H đã cho là tổng diện tích hình chữ nhật và hai nửa hình tròn. Tìm diện tích hình H

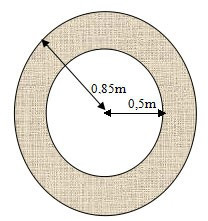
Bài 6: Tính diện tích phần tô đậm hình tròn (xem hình vẽ bên) biết 2 hình tròn có cùng tâm O và có bán kính lần lượt là 0,8 m và 0,5m.

Bài 7: Sân trường em hình chữ nhật có chiều dài 45m và hơn chiều rộng 6,5m. Chính giữa sân có 1 bồn hoa hình tròn đường kính 3,2m. Tính diện tích sân trường còn lại?

Bài 8: Tính diện tích hình thang có đáy lớn bằng 25 m, chiều cao bằng 80% đáy lớn, đáy bé bằng 90% chiều cao.

Bài 9: Có một miếng đất hình bình hành cạnh đáy dài là 32,5m; chiều cao bằng $\frac{2}{3}$ cạnh đáy. Trên miếng đất người ta trồng nhau, mỗi mét vuông đất thu hoạch được 2,4kg rau. Hỏi trên miếng đất đó thu hoạch được tất cả là bao nhiêu ki-lô-gam rau ?

Bài 10: Một miếng đất hình thoi có diện tích bằng 288 m², đường chéo thứ nhất có độ dài 36m, người ta vẽ miếng đất lên bản đồ có tỉ lệ 1 : 400. Hỏi diện tích của hình vẽ trên bản đồ bằng bao nhiêu ?

Bài 11: Cho 5 điểm A, B, C, D, E trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng. Hỏi khi nối các điểm trên ta được bao nhiêu đoạn thẳng?

Bài 12: Để có 10 đoạn thẳng ta cần ít nhất bao nhiêu điểm ?