Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Công thức lượng giác, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Công thức lượng giác. Mời các bạn đón xem:
Bài tập Toán 11 Công thức lượng giác
A. Bài tập Công thức lượng giác
Bài 1. Tính sin2a và tan2a biết cos a = và <a<2.
Hướng dẫn giải
Vì <a<2nên sina < 0.
Ta có:
sin2a + cos2a = 1 ⇒ sin2a = 1 – cos2a = 1 - 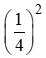
⇒ sina = .
Ta có: sin2a = 2sina cosa = 2.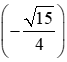
Ta có: tana =
⇒=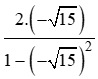
Bài 2. Tính
a) sin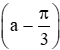
b) cos.cos + sin.sin.
Hướng dẫn giải
a) Vì 0<a< nên cosa > 0.
Ta có: sin2a + cos2a = 1 ⇒ cos2a = 1 – sin2a = 1-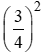
⇒ cosa = null.
Vậy sin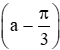
Suy ra: .
Bài 3. Tính
a) cos(–15°) + cos255°;
b) sinsin.
Hướng dẫn giải
a) Ta có:
cos(-15o) + cos255o = 2.cos.cos
= 2.cos120o.cos(135o) = 2
Vậy cos(–15°) + cos255° = .
b) Ta có:
Vậy .
Bài 4. Rút gọn biểu thức sau:
Hướng dẫn giải
⇔
Vậy P = −2sin x.
Bài 5. Chứng minh rằng:
Hướng dẫn giải
Ta có:
Bài 6. Cho và Tính các giá trị lượng giác của góc 2α.
Hướng dẫn giải
Do ⇒ cos α < 0.
Ta có:
⇒ (do cos α < 0).
Bài 7. Tính α + β biết .
Hướng dẫn giải
Áp dụng công thức cộng đối với tang, ta được:
Vậy .
Bài 8. Cho , với . Tính sina, cosa, 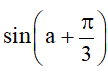
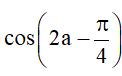
Hướng dẫn giải
Vì nên sina > 0, cosa > 0.
• Áp dụng công thức hạ bậc, ta được:
Suy ra (do sina > 0)
• Áp dụng công thức hạ bậc, ta được: .
Suy ra .
• Áp dụng công thức cộng đối với sin, ta được:
.
• Áp dụng công thức nhân đôi, ta được:
.
• Áp dụng công thức cộng đối với côsin, ta được:
Bài 9. Chứng minh rằng:
a) ;
Hướng dẫn giải
a) VT = cos3x.sinx – sin3x.cosx
= cosx.sinx.(cos2x – sin2x)
= VP.
Vậy ta có điều phải chứng minh.
Bài 10. Cho ∆ABC. Chứng minh rằng:
a) ;
b) ;
c) , với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.
Hướng dẫn giải
∆ABC, có: , suy ra
Do đó .
b)
Vậy ta có điều phải chứng minh.
c) VT = sin2A + sin2B + sin2C
= 2sin(A + B).cos(A – B) + 2sinC.cosC
= 2sin(180° – C).cos(A – B) + 2sinC.cosC
= 2sinC.cos(A – B) + 2sinC.cosC
= 2sinC.[cos(A – B) + cosC]
= 2sinC.[cos(A – B) + cos(180° – A – B)]
= 2sinC.[cos(A – B) – cos(A + B)]
= –4sinC.sinA.sin(–B)
= 4sinA.sinB.sinC
.
Vậy ta có điều phải chứng minh.
Bài 11. Khẳng định nào sau đây đúng?
A. sin(2018a) = 2018sina.cosa.
B. sin(2018a) = 2018sin(1009a).cos(1009a).
C. sin(2018a) = 2sinacosa.
D. sin(2018a) = 2sin(1009a).cos(1009a).
Đáp án đúng là: D
Áp dụng công thức sin2 = 2sin.cos ta được
sin(2018a) = 2sin(1009a).cos(1009a).
Bài 12. Khẳng định nào sai trong các khẳng định sau?
A.
B.
C.
D.
Đáp án đúng là: D
Ta có cos3x = 4cos3x - 3cosx.
Bài 13. Công thức nào sau đây đúng?
A. cos3a = 3cosa - 4cos3a.
B. cos3a = 4cos3a - 3cosa.
C. cos3a = 3cos3a - 4cosa.
D. cos3a = 4cosa - 3cos3a.
Đáp án đúng là: B
Bài 14. Nếu tan(a+b) = 7, tan(a-b) = 4 thì giá trị đúng của tan2a là
A.
B.
C.
D.
Đáp án đúng là: A
Ta có tan2a = tan[(a+b)+(a-b)] =
Bài 15. Cho x, y là các góc nhọn và dương thỏa mãn cotx = , coty = Tổng x+y bằng
A.
B.
C.
D. .
Đáp án đúng là: B
Ta có cot(x+y) =
Mặt khác 0<x,y< suy ra 0<x+y<. Do đó x+y = .
Bài 16. Trong ABC, nếu = 2cosA thì ABC là tam giác có tính chất nào sau đây?
A. Cân tại B.
B. Cân tại A.
C. Cân tại C.
D. Vuông tại B.
Đáp án đúng là: A
Ta có = 2cosAsinB = 2sinC.cosA = sin(C+A)+sin(C-A)
Mặt khác A+B+C = B = -(A+C) sinB = sin(A+C).
Do đó, ta được sin(C-A) = 0A = C.
B. Lý thuyết Công thức lượng giác
1. Công thức cộng
cos (a – b) = cosa cosb + sina sinb
cos (a + b) = cosa cosb – sina sinb
sin (a – b) = sina cosb – cosa sinb
sin (a + b) = sina cosb + cosa sinb
tan (a-b) =
tan (a+b) =
(giả thiết các biểu thức đều có nghĩa).
Ví dụ: Không dùng máy tính, hãy tính sin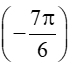
Hướng dẫn giải
Ta có
sin 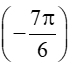
= -sincos - cossin = -0. - (-1). = .
Ta có
tan15o = tan(60o - 45o) =
2. Công thức nhân đôi
sin2a = 2sina cosa
cos2a = cos2a – sin2a = 2cos2 – 1 = 1 – 2sin2a
tan2a = .
Chú ý: Từ công thức nhân đôi suy ra công thức hạ bậc:
.
Ví dụ: Biết sinα = và 0 < α < . Tính sin2α ; cos2α và tan2α.
Hướng dẫn giải
Vì 0 < α < nên cosα > 0.
Ta có:
sin2α + cos2α = 1 ⇒ cos2α = 1 – sin2α = 1-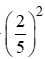
⇒ cosα = .
Ta có: sin2α = 2sinα cosα =
cos2α = 1 – 2sin2α = 1 - 2.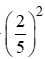
⇒ tan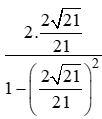
3. Công thức biến đổi tích thành tổng
cosacosb = [cos(a-b) + cos(a+b)]
sinasinb = [cos(a-b) - cos(a+b)]
sinacosb = [sin(a-b) + sin(a+b)].
Ví dụ: Tính giá trị của biểu thức
a) A = ;
b) B = .
Hướng dẫn giải
a) Ta có:
Vậy A = .
b) Ta có:
Vậy B = .
4. Công thức biến đổi tổng thành tích
cosu + cosv = 2coscos
cosu - cosv = -2sinsin
sinu + sinv = 2sincos
sinu - sinv = 2cossin.
Ví dụ: ChoA = cos.cos và B = cos + cos. Không dùng máy tính, tính giá trị của biểu thức .
Hướng dẫn giải
Ta có:
B = cos + cos = 2.cos.cos
= 2.cos.cos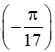
Suy ra .
Video bài giảng Toán 11 Bài 2: Công thức lượng giác - Kết nối tri thức