Với tóm tắt lý thuyết Toán lớp 6 Chương 4: Một số hình phẳng trong thực tiễn sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Chương 4: Một số hình phẳng trong thực tiễn

Video giải Toán 6 Chương 4: Một số hình phẳng trong thực tiễn - Kết nối tri thức

A. Lý thuyết Toán lớp 6 Chương 4: Một số hình phẳng trong thực tiễn

1. Hình tam giác đều

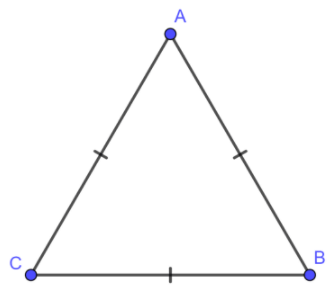
Trong tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng 60⁰C.

2. Hình vuông

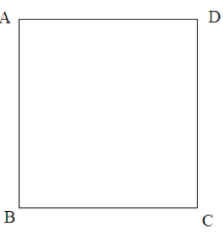
Trong hình vuông:

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng 90⁰.

- Hai đường chéo bằng nhau.

3. Hình lục giác đều

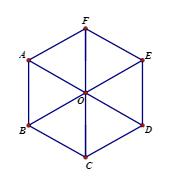
Hình lục giác đều có:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau, mỗi góc bằng 120⁰.

- Ba đường chéo chính bằng nhau.

4. Hình chữ nhật

Trong hình chữ nhật có:

- Bốn góc bằng nhau và bằng 90⁰C.

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

5. Hình thoi

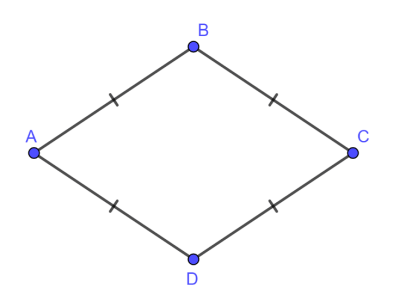
Trong hình thoi :

- Bốn cạnh bằng nhau.

- Hai đường chéo vuông góc với nhau.

- Các cặp góc đối bằng nhau.

6. Hình bình hành

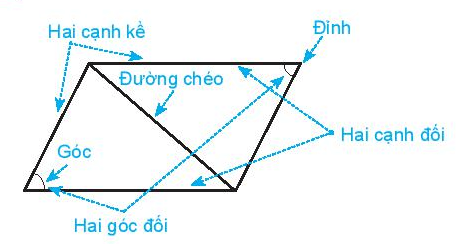
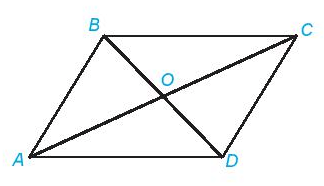
Trong hình bình hành:

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

- Các cặp cạnh đối song song.

- Các cặp góc đối bằng nhau.

7. Hình thang cân

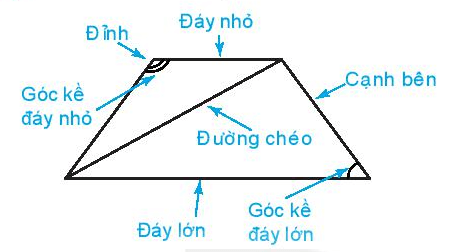
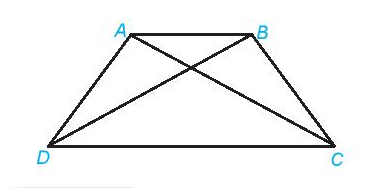
Trong hình thang cân:

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

- Hai cạnh đáy song song với nhau.

- Hai góc kề một đáy bằng nhau.

8. Công thức tính chu vi, diện tích hình vuông, hình chữ nhật và hình thang

Hình vuông cạnh a:

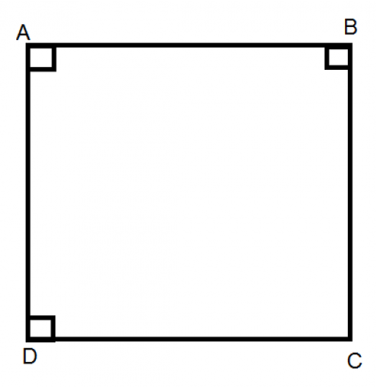
Chu vi: C = 4a.

Diện tích: S = a².

Hình chữ nhật có chiều dài là a, chiều rộng là b:

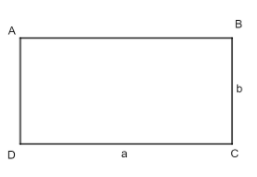
Chu vi: C = 2(a + b).

Diện tích: S = a.b.

Hình thang có độ dài hai cạnh đáy là a, b chiều cao h:

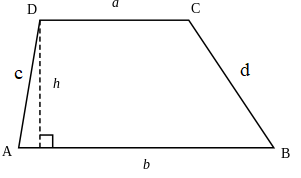
Chu vi: C = a + b + c + d.

Diện tích: S = (a + b).h:2.

9. Chu vi, diện tích hình bình hành, hình thoi.

Hình bình hành: 

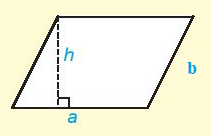
Chu vi: C = 2(a + b).

Diện tích: S = a.h.

Hình thoi:

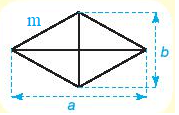
Chu vi: C = 4.m.

Diện tích: S = 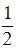ab  .

B. Bài tập

Bài 1. Tính diện tích và chu vi các hình được tô màu sau:

Lời giải

a) 

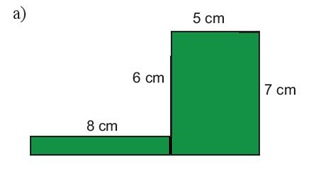
Chu vi của hình đã cho là: 8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).

Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:

Diện tích hình chữ nhật to là: 5.7 = 35(cm²)

Diện tích hình chữ nhật nhỏ là: 8.(7 - 6) = 8(cm²) 

Diện tích hình ban đầu là: 35 + 8 = 43(cm²)

Vậy diện tích hình được tô màu là 43cm² và chu vi hình được tô màu là 40 cm.

b)

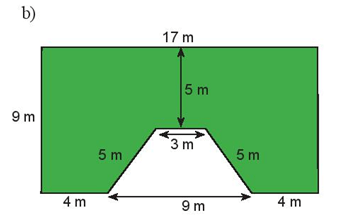
Chu vi hình được tô màu là: 9 + 4 + 5 + 3 + 5 + 4 + 9 + 17 = 56 (m).

Diện tích hình chữ nhật là: 9.17 = 153 (m²).

Diện tích hình thang cân là: (9 + 3).(9 - 5):2 = 24 (m²).

Diện tích phần được tô màu bằng diện tích hình chữ nhật trừ đi diện tích hình thang cân màu trắng. Khi đó diện tích phần tô màu là: 153 - 24 = 129 (m²).

Vậy chu vi hình được tô màu là 56m, diện tích phần tô màu là 129m².

Bài 2. Một mảnh vườn có hình dạng như hình vẽ bên. Để tính diện tích mảnh vườn, người ta chia nó thành hình thang cân ABCD và hình bình hành ADEF có kích thước như sau: BC = 30 m; AD = 42 m, BM = 22 m, EN = 28 m. Hãy tính diện tích mảnh vườn này.

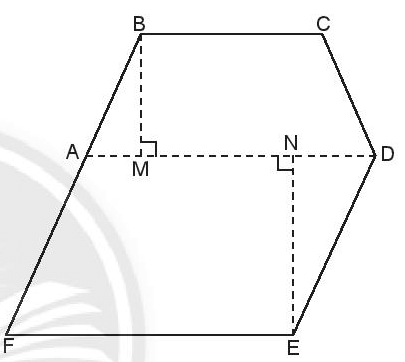
Lời giải

Diện tích hình thang cân ABCD là: (30 + 42).22:2 = 792  (m²).

Diện tích hình bình hành ADEF là: 42.28 = 1176  (m²) 

Diện tích mảnh vườn là: 792 + 1176 = 1968(m²).

Vậy diện tích mảnh vườn là 1968m²

Bài 3. Một khu vườn hình chữ nhật có chiều dài 25 m, chiều rộng 15 m. Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là 5 m và 3 m. Tính diện tích phần còn lại của khu vườn.

Lời giải

Diện tích khu vườn hình chữ nhật là: 25.15 = 375  (m²)

Diện tích bồn hoa hình thoi là: 5.3:2 = 7,5 (m²)

Diện tích phần còn lại của mảnh vườn là: 375 - 7,5 = 367,5 (m²)

Vậy diện tích phần còn lại là 367,5 m².

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Chương 3: Số nguyên

Lý thuyết Chương 4: Một số hình phẳng trong thực tiễn

Lý thuyết Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

Lý thuyết Chương 6: Phân số

Lý thuyết Chương 7: Số thập phân