Với tóm tắt lý thuyết Toán lớp 6 Chương 9: Một số yếu tố xác suất sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Chương 9: Một số yếu tố xác suất

Video giải Toán 6 Chương 9: Một số yếu tố xác suất – Chân trời sáng tạo

A. Lý thuyết Toán lớp 6 Chương 9: Một số yếu tố xác suất

1. Phép thử nghiệm 

Trong các trò chơi (thí nghiệm) tung đồng xu, bốc thăm, gieo xúc xắc, quay xổ số, …, mỗi lần tung đồng xu hay bốc thăm như trên được gọi là một phép thử nghiệm.

Khi thực hiện phép thử nghiệm (trò chơi; thí nghiệm), ta rất khó để dự đoán trước chính xác kết quả của mỗi phép thử nghiệm đó. Tuy nhiên ta có thể liệt kê được tập hợp tất cả các kết quả có thể xảy ra của phép thử nghiệm đó.

2. Sự kiện 

Khi thực hiện phép thử nghiệm, có những sự kiện chắc chắn xảy ra, có những sự kiện không thể xảy ra và cũng có những sự kiện có thể xảy ra.

3. Khả năng xảy ra của một sự kiện 

Khi thực hiện một phép thử nghiệm, một sự kiện có thể xảy ra hoặc không thể xảy ra. Để nói về khả năng xảy ra của mỗi sự kiện, ta dùng một con số có giá trị từ 0 đến 1.

Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.

Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.

4. Xác suất thực nghiệm 

Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số

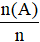 = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động

được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.

B. Bài tập tự luyện

Bài 1. Trong hộp có 1 bóng xanh (X), 1 bóng đỏ (Đ) và 1 bóng trắng (T). Bình lấy ra lần lượt từng bóng, ghi màu quả bóng rồi trả nó lại hộp. Kết quả 8 lần lấy bóng cho ở bảng sau:

a) Hãy cho biết kết quả của lần lấy bóng thứ 2 và thứ 6.

b) Hãy cho biết có bao nhiêu kết quả khác nhau có thể xảy ra trong mỗi lần lấy bóng.

Lời giải: 

a) Dựa vào bảng trên ta xác định được:

- Lần thứ 2 lấy được bóng màu đỏ.

- Lần thứ 6 lấy được bóng màu trắng.

b) Vì trong hộp có 3 màu bóng: xanh, đỏ, trắng.

Nên có thể xảy ra ba kết quả là: lấy được bóng xanh, lấy được bóng đỏ, lấy được bóng trắng.

Ta có thể viết: Tập hợp các kết quả khi lấy ra 1 bóng từ hộp là {X; Đ; T}.

Bài 2. Minh lấy một chiếc bút từ hộp bút có chứa 2 bút chì, 4 bút bi xanh và 1 bút bi đen.

a) Liệt kê tất cả các kết quả có thể.

b) Sự kiện “Minh lấy được bút bi xanh” có luôn xảy ra không?

Lời giải: 

a) Trong hộp bút có ba loại bút: bút chì, bút bi xanh và bút bi đen. Khi Minh lấy một chiếc bút từ hộp bút đó thì có thể rút được một trong ba loại trên.

Vậy các kết quả có thể xảy ra là: Minh lấy được bút chì; Minh lấy được bút bi xanh; Minh lấy được bút bi đen.

b) Theo câu a, các kết quả có thể xảy ra là: Minh lấy được bút chì; Minh lấy được bút bi xanh; Minh lấy được bút bi đen.

Do đó, Minh có thể lấy được bút bi xanh, cũng có thể không lấy được bút bi xanh.

Vậy sự kiện “Minh lấy được bút bi xanh” có thể xảy ra.

Bài 3. Gieo một con xúc xắc 6 mặt cân đối. Hãy đánh giá xem các sự kiện sau là chắc chắn, không thể hay có thể xảy ra.

a) Mặt xuất hiện có số chấm chia hết cho 5.

b) Mặt xuất hiện có số chấm lớn hơn 7.

c) Mặt xuất hiện có số chấm nhỏ hơn 8.

Lời giải: 

Một xúc xắc có 6 mặt tương ứng với các số chấm là 1; 2; 3; 4; 5; 6.

Vậy các khả năng có thể xảy ra là:

Số chấm: 1; 2; 3; 4; 5; 6.

a) Vì trong 6 khả năng trên, mặt có số chấm là 5 thì chia hết cho 5, còn các mặt khác thì không chia hết cho 5. 

Vậy sự kiện “Mặt xuất hiện có số chấm chia hết cho 5” là có thể xảy ra.

b) Vì cả 6 khả năng trên thì số chấm đều nhỏ hơn 7 hay số chấm trên mỗi mặt của con xúc xắc không thể lớn hơn 7.

Vậy sự kiện “Mặt xuất hiện có số chấm lớn hơn 7” không thể xảy ra.

c) Vì cả 6 khả năng trên thì số chấm đều nhỏ hơn 8 nên sự kiện “Mặt xuất hiện có số chấm nhỏ hơn 8” chắc chắn xảy ra.

Bài 4. Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện:

a) Gieo được mặt có 5 chấm.

b) Gieo được mặt có số chẵn chấm.

Lời giải: 

a) Số lần xuất hiện mặt 5 chấm của con xúc xắc 6 mặt trong 50 lần gieo là: 8.

Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có 5 chấm” là: .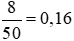

b) Số mặt có chẵn chấm là các mặt có 2 chấm, 4 chấm và 6 chấm.

Số lần xuất hiện mặt 2 chấm là: 6.

Số lần xuất hiện mặt 4 chấm là: 9.

Số lần xuất hiện mặt 6 chấm là: 9.

Do đó, số lần xuất hiện mặt có chẵn chấm của con xúc xắc 6 mặt trong 50 lần gieo là: 6 + 9 + 9 = 24.

Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có số chẵn chấm” là: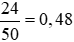 

Bài 5. Trong hộp có một số viên bi màu xanh, đỏ và vàng có kích thước giống nhau. Lấy ngẫu nhiên một viên bi từ hộp, xem màu rồi trả lại lại. Lặp lại hoạt động đó 80 lần ta được kết quả như sau:

a) Tính xác suất thực hiện của sự kiện “lấy được viên bi xanh”.

b) Em hãy dự đoán xem trong hộp loại bi nào có nhiều hơn.

Lời giải: 

a) Số lần lấy được bi xanh trong 80 lần lấy bi từ hộp là 22.

Vậy xác suất thực nghiệm của sự kiện “lấy được viên bi xanh” trong 80 lần lấy là: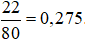 

b) Tổng số viên bi xanh và viên bi vàng là: 22 + 13 = 35 (viên bi)

Ta thấy: số lần lấy được viên bi đỏ nhiều hơn so với số lần lấy được viên bi xanh và viên bi vàng.

Vậy có thể dự đoán là trong hộp đó số viên bi đỏ nhiều hơn số viên bi đỏ và số viên bi vàng.

Bài 6. Số điện thoại một cửa hàng bán được trong 30 ngày của tháng 8 được cho ở bảng sau:

Hãy tính xác suất thực nghiệm của sự kiện:

a) Cửa hàng bán được 5 chiếc điện thoại một ngày.

b) Cửa hàng bán được trên 7 chiếc điện thoại một ngày.

Lời giải:

a) Số ngày cửa hàng bán được 5 chiếc điện thoại trong 30 ngày là 9.

Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được 5 chiếc điện thoại một ngày” là: .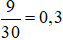

b) Số ngày cửa hàng bán được trên 7 chiếc điện thoại bằng tổng số các ngày cửa hàng bán được 8 chiếc điện thoại, 9 chiếc điện thoại và 12 chiếc điện thoại.

Số ngày cửa hàng bán được 8 chiếc điện thoại là: 3.

Số ngày cửa hàng bán được 9 chiếc điện thoại là: 2.

Số ngày cửa hàng bán được 12 chiếc điện thoại là: 1.

Số ngày cửa hàng bán được trên 7 chiếc điện thoại một ngày trong 30 ngày là: 

3 + 2 + 1 = 6.

Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được trên 7 chiếc điện thoại một ngày” là: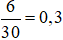 

Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Chương 5: Phân số

Lý thuyết Chương 6: Số thập phân

Lý thuyết Chương 7: Hình học trực quan

Lý thuyết Chương 8: Hình học phẳng và các hình học cơ bản

Lý thuyết Chương 9: Một số yếu tố xác suất