Với tóm tắt lý thuyết Toán lớp 6 Bài 13: Tập hợp các số nguyên sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 13: Tập hợp các số nguyên

Video giải Toán 6 Bài 13: Tập hợp các số nguyên - Kết nối tri thức

A. Lý thuyết Tập hợp các số nguyên

1. Làm quen với số nguyên âm

- Các số tự nhiên (khác 0) 1; 2; 3; 4; … còn được gọi là các số nguyên dương.

- Các số - 1; -2; -3; … gọi là các số nguyên âm.

- Tập hợp gồm các số nguyên âm, số 0 và số nguyên dương gọi là tập hợp số nguyên.

Z = {...; -3; -3; -3; 0; 1; 2; 3;...}.

Chú ý: 

Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.

Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn số 6 còn được viết là +6 (đọc là “dương sáu”).

Ví dụ 1. Các số nguyên nào biểu diễn các đại lượng sau:

a) Đỉnh núi Phan – xi – păng cao 3 147, 3m;

b) Độ sâu của đáy sông Sài Gòn là 20m;

c) Bác An đang nợ 2 triệu đồng.

Lời giải

a) Độ cao củ đỉnh núi Phan – xi – păng được biểu diễn là: 3 147, 3m.

b) Độ sâu của đáy sông Sài Gòn được biểu diễn là: -20 m.

c) Số tiền nợ của bác An được biểu diễn là: - 2 (triệu đồng).

2. Thứ tự trong tập số nguyên

Trục số: 

Ta biểu diễn các số 0; 1; 2; 3; 4; 5 … và các số nguyên âm -1; -2; -3; 4; 5… như sau:

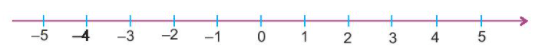
+ Chiều từ trái sang phải là chiều dương, chiều ngược lại là chiều âm.

+ Điểm biểu diễn số nguyên a được gọi là điểm a.

+ Cho hai số nguyên a và b. Trên trục số, nếu điểm a nằm trước điểm b thì số a nhỏ hơn số b, kí hiệu a < b.

Ví dụ 2. Các điểm A, B, C, D và E trong hình biểu diễn những số nào?

Lời giải

Điểm A cách điểm 0 năm đơn vị về bên phải nên A biểu diễn cho số  5;

Điểm C cách điểm 0 bảy đơn vị về bên phải nên C biểu diễn cho số 7;

Điểm B cách điểm 0 bốn đơn vị về bên trái nên B biểu diễn cho số -4;

Điểm E biểu diễn cho điểm – 1; 

Điểm D biểu diễn cho điểm 0;

So sánh hai nguyên:

Mọi số nguyên âm đều nhỏ hơn 0, do đó nhỏ hơn mọi số nguyên dương.

Nếu a, b là hai số nguyên dương và a > b thì – a < - b.

Ví dụ 2. Sắp xếp các số sau theo thứ tự tăng dần:

- 3; 4; -9; 0; -12; 2; 15; 1.

Lời giải

Các số đã cho được sắp xếp theo thứ tự tăng dần là:

-12; -9; -3; 0; 1; 2; 4; 15.

B. Bài tập

Bài 1. Liệt kê các phần tử của mỗi tập hợp sau:

a) B = {x ∈ Z | -3 ≤ x ≤ 4} ;

b) B = {x ∈ Z | -2 ≤ x ≤ 0}.

Lời giải

a) A = {-3; -2; -1; 0; 1; 2; 3}.

b) B = {-2; -1; 0}.

Bài 2. So sánh hai số:

a) -49 và -38;                           b) -1379 và – 2379.

Lời giải

a) Vì 49 > 38 nên -49 < -38.

b) Vì 2379 > 1379 nên -2379 < -1379.

Bài 3. Hãy sử dụng số nguyên âm để diễn tả lại ý nghĩa của các câu sau:

a) Mùa đông ở Siberia (Nga) dài và khắc nghiệt, với nhiệt độ trung bình tháng 1 là 25^oC  dưới 0^oC  .

b) Cá voi xanh có thể lặn sâu 2500m có với mực nước biển.

Lời giải

a) Nhiệt độ trung bình tháng 1 của Siberia (Nga) được biểu diễn là: -25^oC .

b) Độ sâu mà Cá voi xanh có thể lặn được biểu diễn là: – 2500 m.

Bài giảng Toán 6 Bài 13: Tập hợp các số nguyên - Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 12: Bội chung. Bội chung nhỏ nhất

Lý thuyết Bài 13: Tập hợp các số nguyên

Lý thuyết Bài 14: Phép cộng và phép trừ số nguyên

Lý thuyết Bài 15: Quy tắc dấu ngoặc

Lý thuyết Bài 16: Phép nhân số nguyên