Tailieumoi.vn xin giới thiệu bộ đề thi học kì 2 môn Toán lớp 8 sách Kết nối tri thức năm 2024 – 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 2 Toán 8. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 8 Kết nối tri thức bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi học kì 2 Toán 8 Kết nối tri thức có đáp án năm 2025
Đề thi học kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Kết nối tri thức
Năm học 2024 - 2025
Môn: Toán 8
Thời gian làm bài: phút
(Đề số 1)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Sử dụng quy tắc đổi dấu, ta đưa phân thức về dạng phân thức nào sau đây?
A. .
B. .
C. .
D. .
Câu 2. Phép tính có kết quả là
A. .
B. .
C. .
D. .
Câu 3. Vế trái của phương trình 3x + 4 = x+ 12 là
A. x.
B. x + 12.
C. 3x + 4.
D. 3x.
|
Câu 4. Trong mặt phẳng tọa độ Oxy, cho các điểm như trong hình vẽ. Điểm nào là điểm có tọa độ (-2;0)? A. Điểm A. B. Điểm B. C. Điểm C. D. Điểm D. |
|
Câu 5. Giá trị của m để đồ thị hàm số y = (m - 1)x - m + 4 đi qua điểm (2;-3) là
A. m = -5.
B. m = .
C. m = -1.
D. m = .
Câu 6. Đội văn nghệ khối 8 của trường có 3 bạn nam lớp 8A, 3 bạn nữ lớp 8B, 1 bạn nam lớp 8C và 2 bạn nữ lớp 8C. Chọn ngẫu nhiên một bạn trong đội văn nghệ khối 8 để tham gia tiết mục của trường. Số kết quả có thể là
A. 9.
B. 3.
C. 2.
D. 1.
Câu 7. Trong hộp bút của bạn Hoa có 5 bút bi xanh, 3 bút bi đỏ và 2 bút bi đen. Xác suất thực nghiệm của biến cố “Bạn Hoa lấy một bút bi đỏ” là
A. .
B. .
C. .
D. 1.
Câu 8. Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
A. hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
B. ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
C. có hai cặp cạnh tương ứng bằng nhau.
D. hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Câu 9. Cho tam giác DEF vuông tại D. Biểu thức nào đúng trong các biểu thức sau?
|
A. . B. . C. . D. . |
|
Câu 10. Cho ∆ABC; ∆MNP nếu có , , để theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
A. .
B. .
C. .
D. .
Câu 11. Khối rubik ở hình nào có dạng hình chóp tam giác đều?
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Câu 12. Mặt đáy của hình chóp tứ giác đều S.MNPQ là
A. SMN.
B. SPQ.
C. SNP.
D. MNPQ.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Rút gọn các biểu thức sau:
a) A = .
b) A= .
Bài 2. (1,5 điểm) Một xe đạp khởi hành từ điểm A, chạy với vận tốc 15 km/h. Sau đó 6 giờ, một xe hơi đuổi theo với vận tốc 60 km/h. Khi đó, xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?
|
Bài 3. (1,0 điểm) Một đội thanh niên tình nguyện gồm 11 thành viên đến từ các tỉnh, TP như sau: Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk ; Đăk Nông; Lâm Đồng; |
|
TP Hồ Chí Minh, mỗi tỉnh, TP chỉ có đúng một thành viên trong đội. Chọn ngẫu nhiên một thành viên của đội tình nguyện đó.
a) Gọi K là tập hợp gồm các kết quả có thể xảy ra đối với thành viên được chọn. Tính số phần tử của tập hợp K.
b) Tính xác suất của mỗi biến cố sau:
− “Thành viên được chọn ra đến từ vùng Tây Nguyên”.
− “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”.
|
Bài 4. (3,0 điểm) 1. Một hộp quà có dạng là một hình chóp tứ giác đều có cạnh đáy bằng 10 cm, trung đoạn bằng 13 cm. Tính chiều cao của hộp quà. |
|
2. Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau tại điểm H.
a) Chứng minh rằng: ;
b) Cho AB = 4 cm; AC = 5 cm; AD = 2 cm. Tính độ dài đoạn thẳng AE;
c) Chứng minh rằng: .
Bài 5. (0,5 điểm) Tìm giá trị nhỏ nhất của phân thức B = .
−−−−−HẾT−−−−−
ĐÁP ÁN & HƯỚNG DẪN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
D |
C |
C |
B |
A |
A |
B |
A |
A |
B |
A |
D |
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm)
a) A = .
= =
= .
b) B =
=
=
= = .
Bài 2. (1,5 điểm)
Gọi x (h) là thời gian xe hơi chạy đến lúc đuổi kịp xe đạp (x > 0)
Quãng đường xe hơi chạy đến lúc đuổi kịp xe đạp là 60x (km)
Thời gian xe đạp chạy đến lúc gặp xe ô tô là x + 6 (h).
Quãng đường xe đạp chạy đến lúc gặp xe ô tô là 15(x + 6) (km).
Theo đề bài, ta có phương trình
60x = 15(x + 6)
4x = x + 6
3x = 6
x = 2 (TMĐK)
Vậy xe hơi chạy trong 2 h thì đuổi kịp xe đạp.
Bài 3. (1,0 điểm)
a) Tập hợp K gồm các kết quả xảy ra đối với thành viên được chọn là:
K = {Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk; Đăk Nông; Lâm Đồng; TP Hồ Chí Minh}.
Số phần tử của tập hợp K là 11.
b) Có 5 kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Tây Nguyên” đó là Kon Tum; Gia Lai; Đăk Lăk; Đăk Nông; Lâm Đồng.
Vì thế xác suất của biến cố đó là .
+) Có 6 kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Đông Nam Bộ” đó là Bình Phước; Tây Ninh; Bình Dương; Bà Rịa – Vũng Tàu; Đồng Nai; TP Hồ Chí Minh.
Vì thế xác suất của biến cố đó là .
Bài 4. (3,0 điểm)
1.
Ta có SE là trung đoạn nên E là trung điểm của AB.
Xét ∆ABD có E, H lần lượt là trung điểm của AB, BD.
Suy ra EH là đường trung bình của ∆ABD nên = 5 (cm).
Áp dụng định lí Pythagore ∆SEH vuông tại H có:
Suy ra
Do đó SH = 12 cm.
Vậy chiều cao của hộp quà là 12 cm.
|
a) Xét ∆ABD và ∆ACE có" ; Do đó (g.g).
b) Từ câu a: suy ra . Do đó AE = = 2,5 (cm). |
|
Vậy AE = 2,5 (cm).
c) Từ câu a: suy ra hay .
Xét ∆ADE và ∆ABC có:
; (cmt)
Do đó (c.g.c)
Suy ra (hai góc tương ứng) (1)
Mặt khác, ta có:
• (2)
• (3)
Từ (1), (2) và (3) nên suy ra .
Bài 5. (0,5 điểm)
Ta có = = .
Vì nên .
Để phân thức B đạt giá trị nhỏ nhất thì biểu thức đạt giá trị lớn nhất.
Khi đó, B = .
Dấu "=" xảy ra khi và chỉ khi (x + 4)2 = 0 hay x = -4.
Vậy giá trị lớn nhất của phân thức B là khi x = -4.
Đề thi học kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Kết nối tri thức
Năm học 2024 - 2025
Môn: Toán 8
Thời gian làm bài: phút
(Đề số 2)
Câu 1 : Để giải phương trình , một bạn học sinh thực hiện như sau:
Bước 1:
Bước 2:
Bước 3:
Bước 4:
Bước 5.
Bạn học sinh thực hiện giải như vậy là:
Câu 2 : Phương trình nào sau đây không có tập nghiệm là ?
Câu 3 : Cho đường thẳng d là đồ thị của hàm số . Giao điểm của d với trục tung là điểm nào sau đây?
Câu 4 : Cho đường thẳng đi qua điểm . Hệ số góc của đường thẳng d là:
Câu 5 : Một hộp có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Nếu bạn lấy ngẫu nhiên một quả bóng từ hộp, xác suất để lấy được quả bóng màu đỏ là bao nhiêu?
Câu 6 : Trong trận chung kết bóng đá World Cup năm 2022 giữa hai đội Argentina và Pháp, để dự đoán kết quả, người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Argentina, một hộp gắn cờ Pháp và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Pháp thắng.
Câu 7 : Hình chóp tam giác đều và hình chóp tứ giác đều có các mặt bên là các hình gì?
Câu 8 : Một khúc gỗ trang trí có dạng hình chóp tam giác đều. Biết diện tích đáy của khúc gỗ bằng , thể tích của khúc gỗ bằng , chiều cao của khúc gỗ bằng:
Câu 9 : Cho hình vẽ sau, chọn câu trả lời đúng.
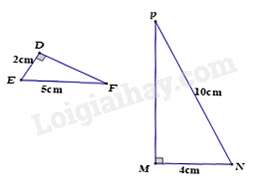
Câu 10 : Cho hình vẽ sau, tỉ số bằng
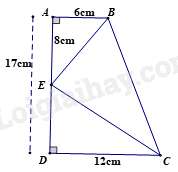
Câu 11 : Cho các khẳng định sau:
(1) Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh.
(2) Hai hình tam giác cân bất kì luôn đồng dạng với nhau.
(3) Hai hình thoi bất kì luôn đồng dạng với nhau.
Số khẳng định đúng là:
Câu 12 : Cho đường tròn (O; 6cm) và đường tròn (O; 3cm). Khi đó, đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng:
Câu 1 : 1. Giải các phương trình sau:
a)
b)
2. Cho hai hàm số và (m là tham số).
a) Với giá trị nào của m thì đồ thị hàm số d’ đi qua điểm
b) Với giá trị nào của m thì đồ thị hàm số trên là hai đường thẳng cắt nhau.
Câu 2 : Giải bài toán bằng cách lập phương trình
Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 25 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 4 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 2 lần số câu trả lời không đúng, kết quả đạt 79 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Câu 3 : 1. Thả một vật dụng không thấm nước hình chóp tứ giác đều như hình bên vào một chiếc bình đang chứa 780 ml nước. Hỏi nước có tràn ra khỏi bình không, biết rằng vật chìm hẳn xuống nước và dung tích của bình là .
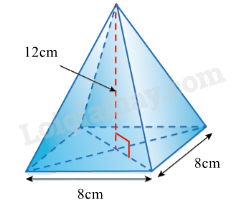
2. Cho có . Qua B dựng đường thẳng cắt AC tại D sao cho .
a) Chứng minh
b) Tính AD và DC.
c) Gọi AH là đường cao của , AE là đường cao của . Chứng minh rằng diện tích gấp 4 lần diện tích .
Câu 4 : Hai ban An và Bình chơi 1 ván oẳn tù tì gồm 12 lần theo luật chơi: Búa (B) thắng Kéo (K), Kéo (K) thẳng Lá (L), Lá (L) thẳng Búa (B) và hòa nhau nếu cùng loại. Sau đây là kết quả của mỗi ván chơi:

Tính xác suất thực nghiệm của biến cố “An không thắng Bình”.
Câu 5 : Giải phương trình .
ĐÁP ÁN
Câu 1 :
Bạn học sinh đã thực hiện sai từ bước 2, nếu muốn khử mẫu thì phải quy đồng cả hai vế, vế bên phải bạn không quy đồng mẫu nên không thể khử mẫu như vậy được.
Đáp án C.
Câu 2 :
suy ra tập nghiệm của phương trình A là .
suy ra tập nghiệm của phương trình B là .
suy ra tập nghiệm của phương trình C là .
suy ra tập nghiệm của phương trình D là .
Đáp án B.
Câu 3 :
Tung độ giao điểm của d với trục tung là:
Vậy giao điểm của d với trục tung là điểm .
Đáp án D.
Câu 4 :
Vì đường thẳng đi qua điểm nên ta có:
Đáp án C.
Câu 5 :
Có tất cả 5 + 3 = 8 quả bóng trong hộp.
Xác suất để lấy được quả bóng màu đỏ là: .
Đáp án A.
Câu 6 :
Vì việc Paul dự đoán đội Argentina hay Pháp thắng là hai biến cố đồng khả năng nên xác suất để Paul dự đoán đội Pháp thắng là .
Đáp án B.
Câu 7 :
Hình chóp tam giác đều và hình chóp tứ giác đều có các mặt bên là hình tam giác cân.
Đáp án B.
Câu 8 :
Ta có công thức tính thể tích hình chóp tam giác đều là:
Chiều cao của khúc gỗ là:
Đáp án C.
Câu 9 :
Xét và có:
nên (cạnh huyền – cạnh góc vuông)
Đáp án C.
Câu 10 :
DE = AD – AE = 17 – 8 = 9(cm)
Xét và có:
Suy ra (hai cạnh góc vuông) suy ra
Đáp án B.
Câu 11 :
Hai hình tròn bất kì luôn là hai hình đồng dạng phối cảnh nên khẳng định (1) đúng.
Hai tam giác cân bất kì luôn đồng dạng là sai vì các góc trong hai tam giác cân có thể khác nhau.
Hai hình thoi bất kì luôn đồng dạng là sai vì các góc trong hai hình thoi có thể khác nhau.
Đáp án B.
Câu 12 :
Đường tròn (O; 6cm) đồng dạng với đường tròn (O; 3cm) theo tỉ số đồng dạng là: .
Đáp án D.
Câu 1 :
1. a)
Vậy z
b)
(vô lý)
Vậy phương trình vô nghiệm.
2. a) Đồ thị hàm số d’ đi qua điểm nên ta có:
Vậy với m = 1 thì đồ thị hàm số d’ đi qua điểm
b) Để hàm số và cắt nhau thì:
1 = m – 2
m = 3
Vậy với m = 3 thì hàm số và cắt nhau.
Câu 2 :
Gọi số câu trả lời không đúng là x .
Vì số câu trả lời đúng gấp 2 lần số câu trả lời không đúng nên số câu trả lời đúng là .
Số câu không trả lời là: .
Vì học sinh có kết quả đạt 79 điểm nên ta có phương trình:
Khi đó số câu trả lời đúng là: (câu)
Số câu không trả lời là: (câu)
Vậy học sinh đó trả lời đúng 12 câu, trả lời không đúng 6 câu và không trả lời 7 câu.
Câu 3 :
1. Thể tích của vật dụng hình chóp tứ giác đều là:
Mà
Sau khi thả vật dụng đó vào chiếc bình thì lượng nước dâng lên thành .
Vậy khi thả vật vào bình thì nước sẽ bị tràn.
2.
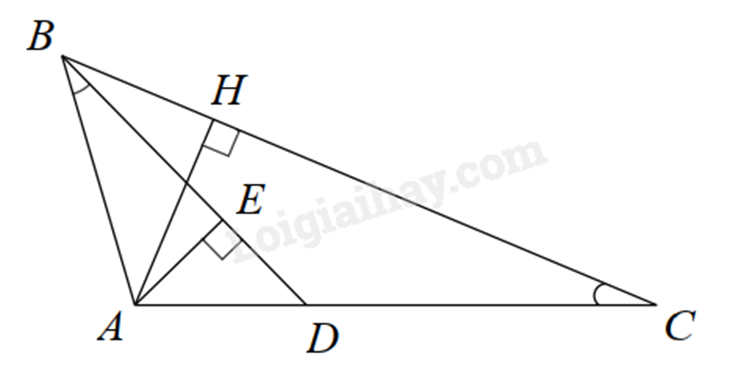
a) Xét và có:
(gt)
chung
Suy ra (g.g). (đpcm)
b) Vì (cmt) suy ra nên .
Suy ra hay .
Suy ra
c) Do suy ra .
Xét và có:
(cmt)
Suy ra suy ra .
Do đó .
Từ đó suy ra(đpcm).
Câu 4 :
Quan sát bảng kết quả ta thấy số lần An thắng Bình là 6 lần.
Do đó số lần An không thắng Bình là: 12 – 6 = 6 (lần)
Vậy xác suất thực nghiệm của biến cố “An không thắng Bình” là: .
Câu 5 :
Trừ các 2 vế cho 14 ta được:
Vậy