Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024

vietjack13 Ngày: 01-04-2024 Lớp 8

Mua tài liệu 4 K

Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 2 môn Toán lớp 8 sách Kết nối tri thức năm 2023 – 2024. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 2 Toán 8. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 2 Toán 8 Kết nối tri thức bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024

Đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 2 - Kết nối tri thức

Năm học 2023 - 2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Biểu thức nào sau đây không phải là phân thức?

A. $\frac{5 x y - 7}{y^{2}}$

B. $5 x y^{2} - 2$

C. $\frac{x^{2} - 2 x + 4}{3 x - 1} .$

D. $\frac{2 x^{2} - x + 1}{\frac{1}{x - y}} .$

Câu 2. Mẫu thức chung của các phân thức $\frac{1}{2 x}; \frac{5}{x^{2}}; \frac{7}{2 x^{3}}$ là

A. $3 x$

B. $4 x^{2}$

C. $5 x^{2}$

D. $2 x^{3}$

Câu 3. Phân thức đối của phân thức $\frac{3}{x + 1}$ là

A. $\frac{3}{x - 1}$

B. $\frac{x + 1}{3}$

C. $- \frac{3}{x + 1}$

D. $\frac{- 3}{- x - 1}$

Câu 4. Phân thức nghịch đảo của phân thức $\frac{2 x}{x + y}$ là

A. $\frac{x + y}{2 x}$

B. $- \frac{2 (x + y)}{x}$

C. $- \frac{x + y}{2 x}$

D. $- \frac{2 x}{x + y}$

Câu 5. Trong các phương trình sau, phương trình nào là phương trình bậc nhất 1 ẩn?

A. $\frac{2}{x} - 3 = 0.$

B. $\frac{- 1}{2} x + 2 = 0.$

C. $x + y = 0.$

D. $0 x + 1 = 0$

Câu 6. Nghiệm của phương trình $12 - 6 x = 0$ là

A. $- 2$

B. $- 6$

C. $2$

D. $6$

Câu 7. Cho tam giác $A B C$ vuông tại $A (A B \neq A C)$ và tam giác $D E F$ vuông tại $D$ $(D E \neq D F) .$ Điều nào dưới đây không suy ra được $Δ A B C ∽ Δ D E F ?$

A. $\hat{B} = \hat{E} .$

B. $\hat{C} = \hat{F} .$

C. $\hat{B} + \hat{C} = \hat{E} + \hat{F} .$

D. $\hat{B} - \hat{C} = \hat{E} - \hat{F} .$

Câu 8. Tam giác $A B C$ vuông cân tại $B$ có độ dài cạnh lớn nhất bằng $10 \sqrt{2} cm .$ Độ dài cạnh $A B$ là

A. $10 \sqrt{2} cm .$

B. $10 cm .$

C. $5 \sqrt{2} cm .$

D. $5 cm .$

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (2,0 điểm) Cho biểu thức:

$P = (\frac{x - 4}{x^{2} - 2 x} + \frac{2}{x - 2}) : (\frac{x + 2}{x} - \frac{x}{x - 2}) .$

a) Tìm điều kiện xác định của biểu thức $P$

b) Tìm $x$ để $P > 0.$

c) Với giá trị nào của $x$ thì giá trị của biểu thức $P$ là số nguyên âm lớn nhất?

Bài 2. (1,0 điểm) Giải các phương trình sau:

a) $x - 3 (2 - x) = 2 x - 4.$

b) $\frac{1}{3} (x - 1) + 4 = \frac{1}{2} (x + 5) .$

Bài 3. (1,5 điểm) Giải bài toán sau bằng cách lập phương trình:

Năm nay tuổi bố gấp 10 lần tuổi của Minh. Bố Minh tính rằng sau 24 năm nữa thì tuổi của bố chỉ gấp 2 lần tuổi của Minh. Hỏi năm nay Minh bao nhiêu tuổi?

Bài 4. (3,0 điểm)

1) Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm $O$ làm cho chú cún cách điểm $O$ xa nhất là $9 m$ Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí $A, B, C, D$ để canh giữ mảnh vườn hình chữ nhật $A B C D$ hay không?

10 Đề thi Giữa kì 2 Toán 8 Kết nối tri thức (có đáp án + ma trận)

2) Cho hình bình hành $A B C D$ có $A C > B D .$ Gọi $H, K$ lần lượt là hình chiếu vuông góc của $C$ trên đường thẳng $A B$ và $A D$ Vẽ tia $D x$ cắt $A C, A B, B C$ lần lượt tại $I, M, N .$ Gọi $J$ là điểm đối xứng với $D$ qua $I$ . Chứng minh:

a) $\frac{C H}{C B} = \frac{C K}{C D} .$

b) $Δ C H K ∽ Δ B C A .$

c) $A B \cdot A H + A D \cdot A K = A C^{2} .$

d) $I M \cdot I N = I D^{2} .$

Bài 5. (0,5 điểm)

Cho $a_{1}; a_{2}; a_{3}; \dots; a_{2023}; a_{2024}$ là 2024 số thực thỏa mãn $a_{k} = \frac{2 k + 1}{{(k^{2} + k)}^{2}}$ với $k \in (1; 2; 3; \dots; 2024) .$

Tính tổng $S_{2024} = a_{1} + a_{2} + a_{3} + \dots + a_{2024} .$

-----HẾT-----

ĐÁP ÁN & HƯỚNG DẪN

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5	6	7	8
Đáp án	D	D	C	A	B	C	C	B

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (2,0 điểm)

a) Ta có:

⦁ $x^{2} - 2 x = x (x - 2) .$

⦁ $\frac{x + 2}{x} - \frac{x}{x - 2}$

$= \frac{(x + 2) (x - 2)}{x (x - 2)} - \frac{x^{2}}{x (x - 2)}$

$= \frac{x^{2} - 4 - x^{2}}{x (x - 2)} = \frac{- 4}{x (x - 2)}$

Khi đó, điều kiện xác định của biểu thức $P$ là:

10 Đề thi Giữa kì 2 Toán 8 Kết nối tri thức (có đáp án + ma trận)

Vậy điều kiện xác định của biểu thức $P$ là $x \neq 0$ và $x \neq 2.$

b) Với $x \neq 0$ và $x \neq 2$ ta có:

$D = (\frac{x - 4}{x^{2} - 2 x} + \frac{2}{x - 2}) : (\frac{x + 2}{x} - \frac{x}{x - 2})$

$= (\frac{x - 4}{x (x - 2)} + \frac{2 x}{x (x - 2)}) : \frac{- 4}{x (x - 2)}$

$= \frac{(x - 4) + 2 x}{x (x - 2)} \cdot \frac{x (x - 2)}{- 4} = \frac{- 3 x + 4}{4} .$

Vì vậy, với $x \neq 0$ và $x \neq 2$ thì $D = \frac{- 3 x + 4}{4} .$

Khi đó $D > 0$ tức là $\frac{- 3 x + 4}{4} > 0,$ do đó $- 3 x + 4 > 0$ vì $4 > 0.$

Suy ra $3 x < 4,$ nên $x < \frac{4}{3} .$

Kết hợp với điều kiện $x \neq 0$ và $x \neq 2,$ ta được $x < \frac{4}{3}$ và $x \neq 0.$

Vậy với $x < \frac{4}{3}$ và $x \neq 0$ thì $D > 0.$

c) Để $D$ là số nguyên âm lớn nhất thì $D = - 1,$ khi đó:

$\frac{- 3 x + 4}{4} = - 1$

$- 3 x + 4 = - 4$

$- 3 x = - 8$

$x = \frac{8}{3}$ (thoả mãn điều kiện).

Vậy với $x = \frac{8}{3}$ thì $D$ có giá trị là số nguyên âm lớn nhất.

Bài 2. (1,0 điểm)

a) $x - 3 (2 - x) = 2 x - 4$

$x - 6 + 3 x = 2 x - 4$

$x + 3 x - 2 x = 6 - 4$

$2 x = 2$

$x = 1$

Vậy phương trình đã cho có nghiệm $x = 1$

b) $\frac{1}{3} (x - 1) + 4 = \frac{1}{2} (x + 5)$

$2 (x - 1) + 24 = 3 (x + 5)$

$2 x - 2 + 24 = 3 x + 15$

$2 x - 3 x = 15 + 2 - 24$

$- x = - 7$

$x = 7$

Vậy phương trình đã cho có nghiệm $x = 7$

Bài 3. (1,5 điểm)

Gọi tuổi của Minh hiện nay là $x (x \in ℕ)$ thì tuổi của bố Minh hiện nay là $10 x .$

Sau 24 năm nữa tuổi của Minh là $x + 24.$

Sau 24 năm nữa tuổi của bố Minh là $10 x + 24.$

Vì sau 24 năm nữa thì tuổi của bố chỉ gấp 2 lần tuổi của Minh nên ta có phương trình:

$10 x + 24 = 2 (x + 24)$

$10 x + 24 = 2 x + 48$

$10 x - 2 x = 48 - 24$

$8 x = 24$

$x = 3$ (thỏa mãn).

Vậy tuổi Minh hiện nay là 3 tuổi.

Bài 4. (3,0 điểm)

1) Áp dụng định lí Pythagore cho các tam giác vuông $A M O,$ $O N C,$ $O M D,$ $O B E,$ ta tính được:

⦁ $O A^{2} = 3^{2} + 4^{2} = 25$ hay $O A = 5 m;$

⦁ $O C^{2} = 6^{2} + 8^{2} = 100$ hay $O C = 10 m;$

⦁ $O D^{2} = 3^{2} + 8^{2} = 73$ hay $O D = \sqrt{73} m;$

⦁ $O B^{2} = 4^{2} + 6^{2} = 52$ hay $O B = \sqrt{52} m.$

Vì $O A = 5 m < 9 m,$ $O D = \sqrt{73} m < 9 m,$ $O B = \sqrt{52} m < 9 m,$ $O C = 10 m > 9 m,$ nên chú cún có thể đến các vị trí $A, D, B$ nhưng không thể đến được vị trí $C$

10 Đề thi Giữa kì 2 Toán 8 Kết nối tri thức (có đáp án + ma trận)

Ta có $A B C D$ là hình bình hành nên $\hat{A B C} = \hat{A D C}$ (1) (tính chất hình bình hành)

Mà $\hat{H B C} = 180 ° - \hat{A B C}$ (2) (hai góc kề bù)

$\hat{K D C} = 180 ° - \hat{A D C}$ (3) (hai góc kề bù)

Từ (1), (2), (3) suy ra $\hat{H B C} = \hat{K D C} .$

Xét $Δ C H B$ và $Δ C K D$ có:

$\hat{B H C} = \hat{D K C} = 90 °$ và $\hat{H B C} = \hat{K D C}$

Do đó $Δ C H B ∽ Δ C K D$ (g.g).

Suy ra $\frac{C H}{C K} = \frac{C B}{C D}$ (tỉ số cạnh tương ứng), hay $\frac{C H}{C B} = \frac{C K}{C D}$ (tính chất tỉ lệ thức).

b) Ta có $\hat{A B C}$ là góc ngoài của $Δ B H C$ nên $\hat{A B C} = \hat{B H C} + \hat{B C H} = 90 ° + \hat{B C H}$ (4)

Vì $A B C D$ là hình bình hành nên $B C // A D$ và $A B = C D$ (tính chất hình bình hành)

Mà $C K ⊥ A D$ nên $C K ⊥ B C$ nên $\hat{B C K} = 90 ° .$

Do đó $\hat{K C H} = \hat{B C K} + \hat{B C H} = 90 ° + \hat{B C H}$ (5)

Từ (4) và (5) suy ra $\hat{A B C} = \hat{K C H} .$

Theo câu a, $\frac{C H}{C B} = \frac{C K}{C D}$

Mà $A B = C D$ nên $\frac{C H}{C B} = \frac{C K}{B A} .$

Xét $Δ C H K$ và $Δ B C A$ có:

$\hat{K C H} = \hat{A B C}$ và $\frac{C H}{C B} = \frac{C K}{B A}$

Do đó $Δ C H K ∽ Δ B C A$ (c.g.c).

c) Kẻ $B E ⊥ A C$ tại $E$ $(E \in A C) .$

Xét $Δ A E B$ và $Δ A H C$ có:

$\hat{A E B} = \hat{A H C} = 90 °$ và $\hat{H A C}$ là góc chung.

Do đó $Δ A E B ∽ Δ A H C$ (g.g).

Suy ra $\frac{A B}{A C} = \frac{A E}{A H}$ (tỉ số cạnh tương ứng) nên $A B \cdot A H = A C \cdot A E$ (6)

Xét $Δ B C E$ và $Δ C A K$ có:

$\hat{B E C} = \hat{C K A} = 90 °$ và $\hat{B C E} = \hat{C A K}$ (hai góc so le trong, $B C // D A$ )

Do đó $Δ B C E ∽ Δ C A K$ (g.g).

Suy ra $\frac{B C}{C A} = \frac{C E}{A K}$ (tỉ số cạnh tương ứng) nên $B C \cdot A K = A C \cdot C E$

Mà $B C = A D$ nên $A D \cdot A K = A C \cdot C E$ (7)

Từ (6) và (7) suy ra:

$A B \cdot A H + A D \cdot A K = A C \cdot A E + A C \cdot C E$

Hay $A B \cdot A H + A D \cdot A K = A C (A E + C E) = A C^{2} .$

Do $A B C D$ là hình bình hành nên $A B // C D; A D // B C$ (tính chất hình bình hành)

Đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 2 - Kết nối tri thức

Năm học 2023 - 2024

Môn: Toán lớp 8

Thời gian làm bài: phút

(Đề số 2)

I. Trắc nghiệm

Khoanh tròn trước câu trả lời đúng.

Câu 1 : Biểu thức nào sau đây không phải là phân thức đại số?

A
$\frac{5 x - 6}{3 x}$ (với $x \neq 0$ ).
B
$\frac{\frac{1}{2 x}}{x + 1}$ (với $x \neq 0; x \neq - 1$ ).
C
$\frac{2 x - 3 y}{x y z}$ (với $x y z \neq 0$ ).
D
$6 x^{2} - 5 x + 7$ .

Câu 2 : Điều kiện xác định của phân thức $\frac{3 x - 5}{2 x + 1}$ là:

A
$x \neq \frac{- 1}{2}$ .
B
$x \neq \frac{1}{2}$ .
C
$x \neq 0$ .
D
$x \neq \frac{5}{3}$ .

Câu 3 : Tính giá trị của phân thức $A (x) = \frac{3}{x - 1}$ với $x \neq 1$ tại x = 2

A
$\frac{1}{3}$ .
B
$- 3$ .
C
$\frac{- 1}{3}$ .
D
$3$ .

Câu 4 : Thực hiện phép tính sau: $\frac{2 x - 3}{7} + \frac{5 x + 3}{7}$ , ta được kết quả là:

A
$x$ .
B
$\frac{- 3 x}{7}$ .
C
$\frac{x}{7}$ .
D
$\frac{3 x}{7}$ .

Câu 5 : Kết quả phép tính $\frac{8 x}{15 y^{3}} : (- \frac{4 x^{2}}{3 y^{2}})$ là

A
$\frac{- 1}{10 x y}$ .
B
$\frac{- 2}{5 x y^{2}}$ .
C
$\frac{- 2}{5 x y}$ .
D
$\frac{2}{5 x y}$ .

Câu 6 : Cho hình vẽ sau, biết $D E / / B C$ , số đo $\hat{A E D}$ là:

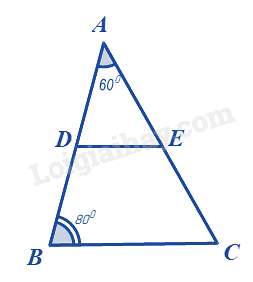
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024 (ảnh 1)

A
$80^{0}$ .
B
$60^{0}$ .
C
$50^{0}$ .
D
$40^{0}$ .

Câu 7 : Đâu là độ dài 3 cạnh của một tam giác vuông:

A
4cm, 7cm, 6cm.
B
6cm, 10cm, 8cm.
C
20cm, 12cm, 25cm.
D
6cm, 11cm, 9cm.

Câu 8 : Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.

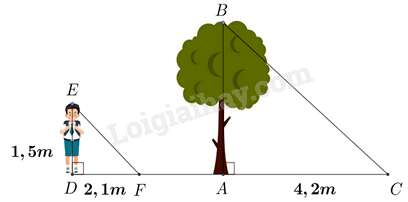
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024 (ảnh 2)

A
$A B = 3 m$ .
B
$A B = 0, 75 m$ .
C
$A B = 2, 4 m$ .
D
$A B = 2, 25 m$ .

II. Tự luận

Câu 1 : Cho $A = (\frac{1}{x - 1} - \frac{1}{x + 1}) . \frac{3 x - 3}{2}$ với $x \neq \pm 1$ .

a) Rút gọn biểu thức A.

b) Tính giá trị của biểu thức A tại x = 2.

c) Với giá trị nguyên nào của x thì A nhận giá trị nguyên.

Câu 2 : Một ca nô xuôi dòng từ bến A đến bến B dài 45 km. Khi ngược dòng từ bến B về bến A, ca nô gặp một ca nô khác tại vị trí C cách bến A 27 km. Biết vận tốc dòng nước là 3km/h. Gọi x (km/h) là tốc độ của ca nô ( x > 3).

a) Viết phân thức biểu thị theo x thời gian ca nô đi từ bến A đến bến B.

b) Viết phân thức biểu thị theo x thời gian ca nô đi từ bến B đến vị trí C.

c) Viết phân thức biểu thị theo x tổng thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C.

Tính tổng thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C nếu vận tốc của ca nô là 12km/h.

Câu 3 : Hai cây B và C được trồng dọc trên đường, cách nhau 18m và cách đều cột đèn D. Ngôi trường A cách cột đèn D 12m theo hướng vuông góc với đường (xem hình vẽ). Tính khoảng cách từ mỗi cây đến ngôi trường.

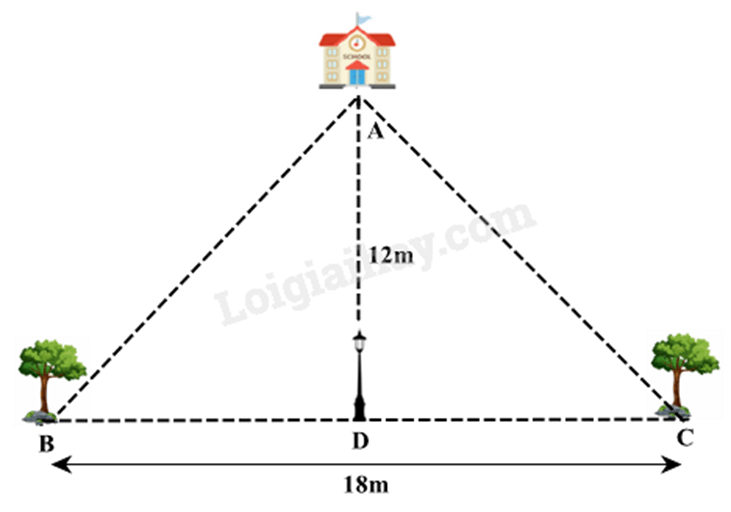
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024 (ảnh 3)

Câu 4 : Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H thuộc BC).

a) Chứng minh $Δ A B H ∽ Δ C B A$ , suy ra $A B^{2} = B H . B C$ .

b) Vẽ $H E ⊥ A B$ tại E, $H F ⊥ A C$ tại F. Chứng minh $A B . A E = A C . A F$ .

c) Chứng minh $Δ A E F ∽ Δ A C B$ .

d) Qua A vẽ đường thẳng song song với BC cắt đường thẳng HF tại I. Vẽ $I N ⊥ B C$ tại N. Chứng minh $Δ H F N ∽ Δ H C I$ .

Câu 5 : Cho $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{a + b + c}$ . Chứng minh rằng:

$\frac{1}{a^{2023}} + \frac{1}{b^{2023}} + \frac{1}{c^{2023}} = \frac{1}{a^{2023} + b^{2023} + c^{2023}}$ .

ĐÁP ÁN

I. Trắc nghiệm

Câu 1 : Đáp án : B

Câu 2 : Đáp án : A

Câu 3 : Đáp án : D

Câu 4 : Đáp án : A

Câu 5 : Đáp án : C

Câu 6 : Đáp án : D

Câu 7 : Đáp án : B

Câu 8 : Đáp án : A

II. Tự luận

Câu 1 :

a) Với $x \neq \pm 1$ , ta có:

$\begin{array}{l} A = (\frac{1}{x - 1} - \frac{1}{x + 1}) . \frac{3 x - 3}{2} \\ = \frac{(x + 1) - (x - 1)}{(x - 1) (x + 1)} . \frac{3 (x - 1)}{2} \\ = \frac{x + 1 - x + 1}{(x - 1) (x + 1)} . \frac{3 (x - 1)}{2} \\ = \frac{2}{(x - 1) (x + 1)} . \frac{3 (x - 1)}{2} \\ = \frac{3}{x + 1} \end{array}$

b) Ta có: $x = 2$ (tmđk) nên thay $x = 2$ vào biểu thức A, ta được:

$A = \frac{3}{2 + 1} = \frac{3}{3} = 1$ .

Vậy A = 1 khi x = 2.

c) Để A nhận giá trị nguyên thì $3 ⋮ (x + 1)$ hay $x + 1 \in U (3)$ . $U (3) = {\pm 1; \pm 3}$ . Ta có bảng giá trị sau:

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024 (ảnh 4)

Vậy $x \in {- 4; - 2; 0; 2}$ thì biểu thức A nhận giá trị nguyên.

Câu 2 :

a) Vì vận tốc của ca nô là x nên vận tốc xuôi dòng của ca nô là x + 3 (km/h)

Vận tốc ngược dòng của ca nô là x -3 (km/h)

Vì ca nô xuôi dòng từ bến A đến bến B nên phân thức biểu thị theo x thời gian ca nô đi từ bến A đến bến B là: $\frac{45}{x + 3}$ .

b) Vì ca nô ngược dòng từ bến B đến vị trí A nên phân thức biểu thị theo x thời gian ca nô đi từ bến B đến vị trí A là: $\frac{45 - 27}{x - 3} = \frac{18}{x - 3}$ .

c) Phân thức biểu thị theo x tổng thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C là: $\frac{45}{x + 3} + \frac{18}{x - 3}$ .

Vì x > 3 nên x = 12 thỏa mãn điều kiện.

Nếu vận tốc của ca nô là 12km/h thì thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C là:

$\frac{45}{12 + 3} + \frac{18}{12 - 3} = 5 (h)$
Vậy nếu vận tốc của ca nô là 12km/h thì thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C là 5h.

Câu 3 :

Vì hai cây B và C được trồng cách đều cột đèn D nên BD = CD = $\frac{1}{2}$ BC = $\frac{1}{2}$ .18 = 9(m)

Vì ngôi trường A cách cột đèn D 12m theo hướng vuông góc nên $\hat{A D C} = 90^{o}$ .

Xét $Δ A B D$ và $Δ A C D$ có:

$A D$ chung

$\hat{A D B} = \hat{A D C} = (90^{0})$

BD = DC (cmt)

$\Rightarrow Δ A B D = Δ A C D$ (hai cạnh góc vuông)

$\Rightarrow A B = A C$

Áp dụng định lí Pythagore vào tam giác vuông ADC, ta có:

$\begin{array}{l} A C^{2} = A D^{2} + D C^{2} = 12^{2} + 9^{2} = 225 \\ \Rightarrow A C = \sqrt{225} = 15 (m) \end{array}$

Vậy khoảng cách từ mỗi cây đến ngôi trường là 15m.

Câu 4 :

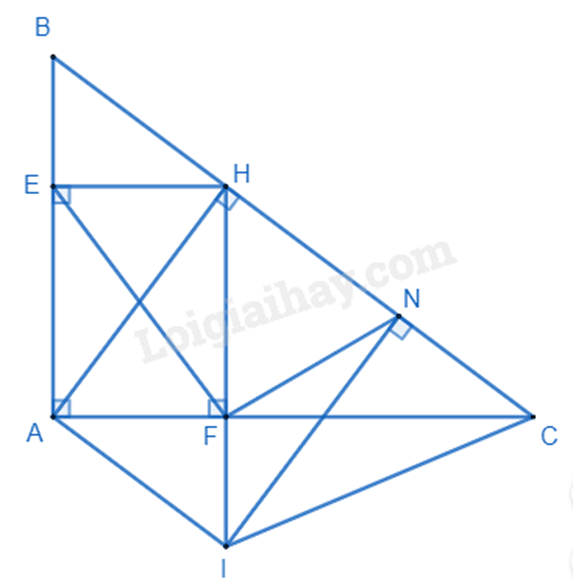
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án năm 2024 (ảnh 5)

a) Xét $Δ A B H$ và $Δ C B A$ có:

$\hat{B}$ chung

$\hat{H} = \hat{A} = (90^{0})$

$\Rightarrow Δ A B H ∽ Δ C B A (g . g)$ (đpcm)

$\Rightarrow \frac{A B}{B H} = \frac{B C}{A B} \Rightarrow A B^{2} = B H . B C$ (đpcm)

b) Xét $Δ A H E$ và $Δ A B H$ có:

$\hat{A}$ chung

$\hat{E} = \hat{H} (= 90^{0})$

$\Rightarrow Δ A H E ∽ Δ A B H (g . g)$

$\Rightarrow \frac{A E}{A H} = \frac{A H}{A B} \Rightarrow A E . A B = A H^{2}$ (1)

Xét $Δ A H F$ và $Δ A C H$ có:

$\hat{A}$ chung

$\hat{F} = \hat{H} (= 90^{0})$

$Δ A H F ∽ Δ A C H (g . g)$

$\Rightarrow \frac{A F}{A H} = \frac{A H}{A C} \Rightarrow A F . A C = A H^{2}$ (2)

Từ (1) và (2) suy ra AE.AB = AF.AC (đpcm)

c) Theo ý b, ta có $A E . A B = A F . A C \Rightarrow \frac{A E}{A F} = \frac{A C}{A B}$ .

Xét $Δ A E F$ và $Δ A C B$ có:

$\hat{A}$ chung

$\frac{A E}{A F} = \frac{A C}{A B}$ (cmt)

$\Rightarrow Δ A E F ∽ Δ A C B$ (c.g.c) (đpcm)

d) Xét $Δ H N I$ và $Δ H F C$ có:

$\hat{H}$ chung

$\hat{N} = \hat{F} = (90^{0})$

$\Rightarrow Δ H N I ∽ Δ H F C (g . g)$

$\Rightarrow \frac{H N}{H I} = \frac{H F}{H C}$

Xét $Δ H F N$ và $Δ H C I$ có:

$\hat{H}$ chung

$\frac{H N}{H I} = \frac{H F}{H C}$ (cmt)

$\Rightarrow Δ H F N ∽ Δ H C I (c . g . c)$ (đpcm)

Câu 5 :

Theo đề bài ta có:

$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{a + b + c}$

$\begin{array}{l} \frac{b c + a c + a b}{a b c} = \frac{1}{a + b + c} \\ (b c + a c + a b) (a + b + c) = a b c \\ b c (a + b) + b c^{2} + a c (a + b) + a c^{2} + a b (a + b) + a b c - a b c = 0 \\ b c (a + b) + a c (a + b) + a b (a + b) + (b c^{2} + a c^{2}) = 0 \\ b c (a + b) + a c (a + b) + a b (a + b) + c^{2} (a + b) = 0 \\ (b c + a c + a b + c^{2}) (a + b) = 0 \\ [(b c + a b) + (a c + c^{2})] (a + b) = 0 \\ [b (a + c) + c (a + c)] (a + b) = 0 \\ (b + c) (a + c) (a + b) = 0 \\ \Rightarrow [\begin{array}{l} b + c = 0 \\ a + c = 0 \\ a + b = 0 \end{array} \\ \Rightarrow [\begin{array}{l} b = - c \\ a = - c \\ a = - b \end{array} \end{array}$

Trường hợp 1. Với $b = - c$ , ta có:

$\begin{array}{l} V T = \frac{1}{a^{2023}} + \frac{1}{b^{2023}} + \frac{1}{c^{2023}} \\ = \frac{1}{a^{2023}} + \frac{1}{{(- c)}^{2023}} + \frac{1}{c^{2023}} \\ = \frac{1}{a^{2023}} - \frac{1}{c^{2023}} + \frac{1}{c^{2023}} \\ = \frac{1}{a^{2023}} \end{array}$

$\begin{array}{l} V P = \frac{1}{a^{2023} + b^{2023} + c^{2023}} \\ = \frac{1}{a^{2023} + {(- c)}^{2023} + c^{2023}} \\ = \frac{1}{a^{2023} - c^{2023} + c^{2023}} \\ = \frac{1}{a^{2023}} \end{array}$