Với tóm tắt lý thuyết Toán lớp 5 Ôn tập: So sánh hai phân số (tiếp theo) hay nhất, chi tiết cùng 10 bài tập chọn lọc sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 5.

Lý thuyết Ôn tập: So sánh hai phân số (tiếp theo) lớp 5 hay, chi tiết

A. Lý thuyết So sánh hai phân số (tiếp)

4) Một số cách so sánh khác

Dạng 1: So sánh với 1

Điều kiện áp dụng:  Phương pháp này áp dụng cho dạng bài so sánh hai phân số, trong đó một phân số bé hơn 1 và một phân số lớn hơn 1.

Ví dụ: So sánh hai phân số 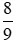và 

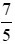
Cách giải:

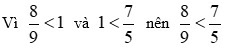
Dạng 2: So sánh với phân số trung gian

Điều kiện áp dụng: Phương pháp này áp dụng khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc ngược lại. Khi đó ta so sánh với phân số trung gian là phân số có tử số bằng tử số của phân số thứ nhất, có mẫu số bằng mẫu số của phân số thứ hai hoặc ngược lại.

Phương pháp giải:

Bước 1: Chọn phân số trung gian.

Bước 2: So sánh hai phân số ban đầu với phân số trung gian.

Bước 3: Rút ra kết luận.

Lưu ý: So sánh hai phân số 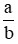và 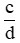(a, b, c, d  khác 0).

Nếu a > c và b < d (hoặc a < c và b > d  thì ta có thể chọn phân số trung gian là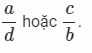 

Ví dụ: So sánh hai phân số 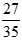và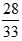 

Cách giải:

Dạng 3: So sánh bằng phần bù

Điều kiện áp dụng: Nhận thấy mẫu số lớn hơn tử số ( phân số bé hơn 1) và hiệu của mẫu số với tử số của tất cả các phân số đều bằng nhau hoặc nhỏ thì ta tìm phần bù với 1.

Chú ý: Phần bù với 1 của phân số là hiệu giữa 1 và phân số đó.

Quy tắc: Trong hai phân số, phân số nào có phần bù lớn hơn thì phân số đó nhỏ hơn và ngược lại phân số nào có phần bù nhỏ hơn thì phân số đó lớn hơn .

Phương pháp giải:

Bước 1: Tìm phần bù của hai phân số.

Bước 2: So sánh hai phần bù với nhau.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số 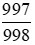và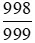 

Cách giải:

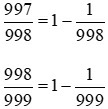
Vì 998 < 999 nên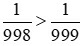 . Do đó, 

Do đó,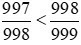 

Dạng 4: So sánh bằng phần hơn

Điều kiện áp dụng: Nhận thấy tử số lớn hơn mẫu số ( phân số lớn hơn 1) và hiệu của tử số với mẫu số của tất cả các phân số đều bằng nhau hoặc nhỏ thì ta tìm phần hơn với 1.

Chú ý: Phần hơn với 1 của phân số là hiệu giữa phân số đó và 1.

Quy tắc: Trong hai phân số, phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn và ngược lại phân số nào có phần hơn nhỏ hơn thì phân số đó nhỏ hơn.

Phương pháp giải:

Bước 1: Tìm phần hơn của hai phân số.

Bước 2: So sánh hai phần hơn với nhau.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số 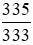và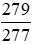 

Giải

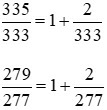
Vì 333 > 277 nên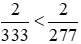 . Do đó,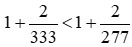 

Vậy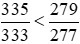 

B. Bài tập So sánh hai phân số (tiếp)

Câu 1: Khi so sánh hai phân số 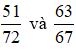 ta có thể chọn phân số trung gian là:

Câu 2: Chọn dấu thích hợp để điền vào ô trống: 

A. =

B. >

C. <

Câu 3: Chọn phân số lớn hơn hai phân số sau:

Câu 4: Chọn dấu thích hợp để điền vào ô trống: 

A. >

B. <

C. =

Câu 5: Chọn dấu thích hợp để điền vào chỗ chấm: 

A. >

B. <

C. =

Câu 6: Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với 1?

A. Khi hai phân số đều bé hơn 1

B. Khi hai phân số đều lớn hơn 1

C. Khi một phân số bé hơn 1 và một phân số lớn hơn 1

D. Khi hai phân số đều bằng 1

Câu 7: Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian?

A. Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai.

B. Khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu của phân số thứ hai.

C. Cả A và B đều sai.

D. Cả A và B đều đúng.

Câu 8: Phần bù 1 của phân số 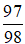 là:

Câu 9: Phần hơn với 1 của phân số 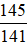 là:

Câu 10: Chọn dấu thích hợp để điền vào ô trống: 

A. =

B. <

C. >