Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 11 sách Cánh diều năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 1 Toán 11. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 11 Cánh diều bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi học kì 1 Toán 11 Cánh diều có đáp án năm 2024
Đề thi học kì 1 Toán 11 Cánh diều có đáp án - Đề 1
A. Ma trận, đặc tả đề kiểm tra cuối học kì 1
MÔN: TOÁN, LỚP 11 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 35 câu (70%)
Câu hỏi tự luận : 3 câu (30%)
|
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ nhận thức |
Tổng |
% tổng điểm |
||||||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
Số CH |
Thời gian (phút) |
|||||||||
|
Số CH |
Thời gian (phút) |
Số CH |
Thời gian (phút) |
Số CH |
Thời gian (phút) |
Số CH |
Thời gian (phút) |
TN |
TL |
|||||
|
1 |
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC |
1.1. Góc lượng giác. Giá trị lượng giác của góc lượng giác |
2 |
2 |
|
|
|
|
|
|
2 |
|
13
|
18
|
|
1.2. Các phép biến đổi lượng giác |
1 |
1 |
1 |
1 |
|
|
|
|
2 |
|
||||
|
1.3. Hàm số lượng giác và đồ thị |
1 |
1 |
1 |
3 |
|
|
|
|
2 |
|
||||
|
1.4. Phương trình lượng giác cơ bản |
2 |
2 |
1 |
3 |
|
|
|
|
3 |
|
||||
|
2 |
DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN |
2.1. Dãy số |
1 |
1 |
1 |
2 |
|
|
1 |
10 |
2 |
1 |
21
|
22 |
|
2.2. Cấp số cộng |
1 |
2 |
1 |
2 |
|
|
2 |
|||||||
|
2.3. Cấp số nhân |
1 |
2 |
1 |
2 |
|
|
2 |
|||||||
|
3 |
GIỚI HẠN. HÀM SỐ LIÊN TỤC |
3.1. Giới hạn của dãy số |
1 |
1 |
1 |
2 |
1 |
9 |
|
|
2 |
1 |
20 |
24 |
|
3.2. Giới hạn của hàm số |
1 |
1 |
1 |
2 |
|
|
2 |
|||||||
|
3.3. Hàm số liên tục |
2 |
2 |
1 |
3 |
|
|
3 |
|
|
|
||||
|
4 |
ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG |
4.1. Đường thẳng và mặt phẳng trong không gian |
1 |
2 |
1 |
2 |
1 |
11 |
|
|
2 |
1 |
36 |
36 |
|
4.2. Hai đường thẳng song song trong không gian |
1 |
1 |
1 |
3 |
|
|
2 |
|||||||
|
4.3. Đường thẳng và mặt phẳng song song |
2 |
2 |
1 |
2 |
|
|
3 |
|||||||
|
4.4. Hai mặt phẳng song song |
1 |
2 |
1 |
3 |
|
|
2 |
|||||||
|
4.5. Hình lăng trụ và hình hộp |
1 |
2 |
1 |
3 |
|
|
2 |
|
||||||
|
4.6. Phép chiếu song song. Hình biểu diễn của một hình không gian |
1 |
1 |
1 |
2 |
|
|
2 |
|
||||||
|
Tổng |
|
20 |
25 |
15 |
35 |
2 |
20 |
1 |
10 |
35 |
3 |
90 |
|
|
|
Tỉ lệ (%) |
|
40 |
30 |
20 |
10 |
70 |
30 |
|
100 |
|||||
|
Tỉ lệ chung (%) |
|
70 |
30 |
|
|
|||||||||
Lưu ý:
– Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.
– Số điểm tính cho 1 câu trắc nghiệm là 0,2 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
MÔN: TOÁN, LỚP 11 – THỜI GIAN LÀM BÀI: 90 phút
|
TT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ nhận thức |
|||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC |
1.1. Góc lượng giác. Giá trị lượng giác của góc lượng giác |
Nhận biết: – Nhận biết các khái niệm cơ bản về góc lượng giác. – Nhận biết khái niệm giá trị lượng giác của một góc lượng giác. |
2 |
|
|
|
|
1.2. Các phép biến đổi lượng giác |
Nhận biết: – Nhận biết các công thức biến đổi lượng giác cơ bản. Thông hiểu: – Mô tả các phép biến đổi lượng giác cơ bản: công thức cộng; công thức góc nhân đôi; công thức biến đổi tích thành tổng và công thức biến đổi tổng thành tích. |
1 |
1 |
||||
|
1.3. Hàm số lượng giác và đồ thị
|
Nhận biết: – Nhận biết các khái niệm về hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. – Nhận biết các đặc trưng hình học của đồ thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. – Nhận biết các hàm số lượng giác, thông qua đường tròn lượng giác. Thông hiểu: – Mô tả bảng giá trị của bốn hàm số lượng giác \(y = \sin x,\) \(y = \cos x,\) \(y = \tan x,\) \(y = \cot x\) trên một chu kì. – Mô tả bốn đồ thị hàm số lượng giác \(y = \sin x,\) \(y = \cos x,\) \(y = \tan x,\) \(y = \cot x.\) – Giải thích tập xác định; tập giá trị; tính chất chẵn, lẻ; tính tuần hoàn; chu kì; khoảng đồng biến, nghịch biến của các hàm số lượng giác dựa vào đồ thị. |
1 |
1 |
||||
|
1.4. Phương trình lượng giác cơ bản |
Nhận biết: – Nhận biết khái niệm phương trình tương đương. – Nhận biết công thức nghiệm của phương trình lượng giác cơ bản bằng cách vận dụng đồ thị hàm số lượng giác tương ứng. Thông hiểu: – Giải một số phương trình lượng giác cơ bản và tính nghiệm gần đúng của phương trình lượng giác cơ bản (có sử dụng máy tính cầm tay). |
2 |
1 |
||||
|
2 |
DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN |
2.1. Dãy số |
Nhận biết: – Nhận biết dãy số hữu hạn, dãy số vô hạn. – Nhận biết tính chất tăng, giảm, bị chặn của dãy số trong những trường hợp đơn giản. Thông hiểu: – Thể hiện được cách cho dãy số bằng liệt kê các số hạng; bằng công thức tổng quát; bằng hệ thức truy hồi; bằng cách mô tả. Vận dụng cao: – Giải quyết một số vấn đề gắn với dãy số. |
1 |
1 |
|
1 |
|
2.2. Cấp số cộng |
Nhận biết: – Nhận biết một dãy số là cấp số cộng. – Nhận biết số hạng đầu và công sai của cấp số cộng. Thông hiểu: – Giải thích công thức xác định số hạng tổng quát của cấp số cộng. – Tính toán một số yếu tố trong cấp số cộng khi biết trước các số hạng. – Tính tổng của \(n\) số hạng đầu của cấp số cộng. Vận dụng cao: – Giải quyết một số vấn đề gắn với cấp số cộng. |
1 |
1 |
|
|||
|
2.3. Cấp số nhân |
Nhận biết: – Nhận biết một dãy số là cấp số nhân. – Nhận biết số hạng đầu và công bội của cấp số nhân. Thông hiểu: – Giải thích công thức xác định số hạng tổng quát của cấp số nhân. – Tính toán một số yếu tố trong cấp số nhân khi biết trước các số hạng. – Tính tổng của \(n\) số hạng đầu của cấp số nhân. Vận dụng cao: – Giải quyết một số vấn đề gắn với cấp số nhân. |
1 |
1 |
|
|||
|
3 |
GIỚI HẠN. HÀM SỐ LIÊN TỤC |
3.1. Giới hạn của dãy số |
Nhận biết: – Nhận biết khái niệm giới hạn của dãy số. Thông hiểu: – Giải thích một số giới hạn cơ bản. Vận dụng: – Vận dụng các phép toán giới hạn dãy số để tìm giới hạn của một số dãy số đơn giản. |
1 |
1 |
1 |
|
|
3.2. Giới hạn của hàm số |
Nhận biết: – Nhận biết khái niệm giới hạn hữu hạn của hàm số, giới hạn hữu hạn một phía của hàm số tại một điểm. – Nhận biết khái niệm giới hạn hữu hạn của hàm số tại vô cực. – Nhận biết khái niệm giới hạn vô cực (một phía) của hàm số tại một điểm. Thông hiểu: – Mô tả một số giới hạn hữu hạn của hàm số tại vô cực cơ bản. – Hiểu được một số giới hạn vô cực (một phía) của hàm số tại một điểm cơ bản. Vận dụng: – Tính một số giới hạn hàm số bằng cách vận dụng các phép toán trên giới hạn hàm số. |
1 |
1 |
|
|
||
|
3.3. Hàm số liên tục |
Nhận biết: – Nhận dạng được hàm số liên tục tại một điểm, hoặc trên một khoảng, hoặc trên một đoạn. – Nhận dạng được tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục. – Nhận biết được tính liên tục của một số hàm sơ cấp cơ bản (như hàm đa thức, hàm phân thức, hàm căn thức, hàm lượng giác) trên tập xác định của chúng. Thông hiểu: – Hiểu được các tính chất của hàm số liên tục tại một điểm, hoặc trên một khoảng, hoặc trên một đoạn; tính liên tục của tổng, hiệu, tích thương của hai hàm số liên tục. |
2 |
1 |
|
|
||
|
4 |
ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG |
4.1. Đường thẳng và mặt phẳng trong không gian |
Nhận biết: – Nhận biết các quan hệ liên thuộc cơ bản giữa điểm, đường thẳng, mặt phẳng trong không gian. – Nhận biết được hình chóp, hình tứ diện. Thông hiểu: – Mô tả được ba cách xác định mặt phẳng: qua ba điểm không thẳng hàng; qua một đường thẳng và một điểm không thuộc đường thẳng đó; qua hai đường thẳng cắt nhau. Vận dụng: – Xác định giao tuyến của hai mặt phẳng; giao điểm của đường thẳng và mặt phẳng. – Vận dụng các tính chất về giao tuyến của hai mặt phẳng; giao điểm của đường thẳng và mặt phẳng vào giải bài tập. |
1 |
1 |
1 |
|
|
4.2. Hai đường thẳng song song trong không gian |
Nhận biết: – Nhận biết vị trí tương đối của hai đường thẳng trong không gian: hai đường thẳng trùng nhau, song song, cắt nhau, chéo nhau trong không gian. Thông hiểu: – Giải thích các tính chất cơ bản về hai đường thẳng song song trong không gian. Vận dụng: – Vận dụng các tính chất của hai đường thẳng song song vào giải bài tập. |
1 |
1 |
|
|||
|
4.3. Đường thẳng và mặt phẳng song song |
Nhận biết: – Nhận biết đường thẳng song song với mặt phẳng. Thông hiểu: – Giải thích được điều kiện để đường thẳng song song với mặt phẳng. – Giải thích được tính chất cơ bản về đường thẳng song song với mặt phẳng. Vận dụng: – Xác định vị trí tương đối giữa đường thẳng và mặt phẳng. – Chứng minh một đường thẳng song song với một mặt phẳng. |
2 |
1 |
|
|||
|
4.4. Hai mặt phẳng song song |
Nhận biết: – Nhận biết hai mặt phẳng song song trong không gian. Thông hiểu: – Giải thích điều kiện để hai mặt phẳng song song. – Giải thích tính chất cơ bản về hai mặt phẳng song song. – Giải thích định lí Thalès trong không gian. – Giải thích tính chất cơ bản của lăng trụ và hình hộp. Vận dụng: – Chứng minh hai mặt phẳng song song. – Vận dụng định lí Thalés và các tính chất của hình lăng trụ, hình hộp vào giải bài tập. |
1 |
1 |
|
|||
|
4.5. Hình lăng trụ và hình hộp |
Nhận biết: – Nhận biết hình lăng trụ và hình hộp. Thông hiểu: – Giải thích được tính chất cơ bản của hình lăng trụ và hình hộp Vận dụng: – Vận dụng được kiến thức về quan hệ song song để mô tả một số hình ảnh trong thực tiễn. |
1 |
1 |
|
|||
|
4.6. Phép chiếu song song. Hình biểu diễn của một hình không gian |
Nhận biết: – Nhận biết được khái niệm và các tính chất cơ bản về phép chiếu song song. Thông hiểu: – Mô tả hình ảnh của một điểm, một đoạn thẳng, một tam giác, một đường tròn qua một phép chiếu song song. |
1 |
1 |
|
|||
|
|
|
|
20 |
15 |
2 |
1 |
|
B. Đề kiểm tra cuối học kì 1
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 1)
I. Trắc nghiệm (7 điểm)
Câu 1. Góc lượng giác có số đo \( - 3\,\,060^\circ \) thì có số đo theo rađian là
A. 17.
B. \(8,5\pi .\)
C. \( - 8,5\pi .\)
D. \( - 17\pi .\)
Câu 2. Cho \(\alpha \) thỏa mãn \(\cos \alpha = \frac{{12}}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi .\) Giá trị của \(\sin \alpha \) bằng
A. \(\frac{1}{{13}}.\)
B. \(\frac{5}{{13}}.\)
C. \( - \frac{5}{{13}}.\)
D. \( - \frac{1}{{13}}.\)
Câu 3. Khẳng định nào dưới đây là khẳng định đúng?
A. \(\cos \left( {a + b} \right) = \cos a\sin b - \sin a\cos b.\)
B. \(\sin \left( {a + b} \right) = \sin a\cos b + \sin b\cos a.\)
C. \(\cos \left( {a + b} \right) = \cos a\cos b + \sin a\sin b.\)
D. \(\sin \left( {a + b} \right) = \sin a\sin b + \cos a\cos b.\)
Câu 4. Rút gọn biểu thức \(P = {\left[ {\tan \frac{{17\pi }}{4} + \tan \left( {\frac{{7\pi }}{2} - x} \right)} \right]^2} + {\left[ {\cot \frac{{13\pi }}{4} + \cot \left( {7\pi - x} \right)} \right]^2}\) ta được kết quả là
A. \(\frac{1}{{{{\sin }^2}x}}.\)
B. \(\frac{1}{{{{\cos }^2}x}}.\)
C. \(\frac{2}{{{{\sin }^2}x}}.\)
D. \(\frac{2}{{{{\cos }^2}x}}.\)
Câu 5. Tập giá trị của hàm số \(y = 2\cos 2x + 1\) là
A. \(\left[ { - 3;1} \right].\)
B. \(\left[ {1;3} \right].\)
C. \(\left[ { - 3; - 1} \right].\)
D. \(\left[ { - 1;3} \right].\)
Câu 6. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. \(y = \sqrt 3 \cos 3x.\)
B. \(y = \cos x.\)
C. \(y = \tan x.\)
D. \(y = {x^2}.\)
Câu 7. Công thức nghiệm của phương trình \(\sin x = \sin \alpha \) là
A. \[\left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\].
B. \[\left[ \begin{array}{l}x = \alpha + k\pi \\x = \pi - \alpha + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\].
C. \[x = \pm \alpha + k2\pi \,\left( {k \in \mathbb{Z}} \right).\]
D. \[x = \alpha + k\pi \,\left( {k \in \mathbb{Z}} \right).\]
Câu 8. Nghiệm của phương trình \(\tan \left( {x - \frac{\pi }{3}} \right) = 1\) là
A. \(x = \frac{{7\pi }}{{12}} + k\pi ,\,k \in \mathbb{Z}.\)
B. \(x = \frac{\pi }{4} + k2\pi ,\,k \in \mathbb{Z}.\)
C. \(x = - \frac{\pi }{{12}} + k\pi ,\,k \in \mathbb{Z}.\)
D. \(x = \frac{\pi }{3} + k\pi ,\,k \in \mathbb{Z}.\)
Câu 9. Trong các phương trình sau đây, phương trình nào vô nghiệm?
A. \(\tan x = \pi .\)
B. \(\cot 2x = - 2.\)
C. \(\sin 2x = \frac{{2024}}{{2024}}.\)
D. \(\cos x = \frac{3}{2}.\)
Câu 10. Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{ - n + 1}}{n}.\) Năm số hạng đầu tiên của dãy số \(\left( {{u_n}} \right)\) lần lượt là
A. \( - \frac{1}{2};\,\, - \frac{2}{3};\, - \frac{3}{4};\,\, - \frac{4}{5};\,\, - \frac{5}{6}.\)
B. \(\frac{1}{2};\,\,\frac{2}{3};\,\,\frac{3}{4};\,\,\frac{4}{5};\,\,\frac{5}{6}.\)
C. \(0;\,\, - \frac{1}{2};\,\, - \frac{2}{3};\, - \frac{3}{4};\,\, - \frac{4}{5}.\)
D. \( - \frac{2}{3};\,\, - \frac{3}{4}; - \,\,\frac{4}{5};\,\, - \frac{5}{6};\,\, - \frac{6}{7}.\)
Câu 11. Trong các dãy số \[\left( {{u_n}} \right)\] cho bởi số hạng tổng quát \({u_n}\) sau, dãy số nào là dãy số tăng?
A. \[{u_n} = \frac{1}{{{2^n}}}.\]
B. \[{u_n} = \frac{1}{n}.\]
C. \[{u_n} = \frac{{n + 5}}{{3n + 1}}.\]
D. \[{u_n} = \frac{{2n - 1}}{{n + 1}}.\]
Câu 12. Trong các dãy số sau, dãy số nào là một cấp số cộng?
A. \(1;\,\, - 4;\,\, - 9;\,\, - 14;\,\, - 19.\)
B. \(1;\,\,4;\,\,6;\,\,7;\,\,10.\)
C. \(1;\,\,0;\,\,0;\,\,0;\,\,0.\)
D. \(3;\,\,9;\,\,27;\,\,81;\,\,243.\)
Câu 13. Cho hình vẽ dưới đây. Các số hạng được viết trong các ô vuông từ trái sang phải tạo thành cấp số cộng. Giá trị của \(x\) trong hình vẽ đã cho là
|
\(2\) |
|
|
\(x\) |
\( - 10\) |
A. \( - 4.\) B. 7.
C. 4. D. \( - 7.\)
Câu 14. Cho dãy số \(\left( {{u_n}} \right)\) biết \(\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = 3{u_n}\end{array} \right.,\forall n \in {\mathbb{N}^*}\). Tìm số hạng tổng quát của dãy số \(\left( {{u_n}} \right).\)
A. \({u_n} = {3^{n - 1}}.\)
B. \({u_n} = {3^{n + 1}}.\)
C. \({u_n} = {3^n}.\)
D. \({u_n} = {n^{n - 1}}.\)
Câu 15. Cho ba số \(1;\,\,2;\,\, - 2a\) theo thứ tự lập thành cấp số nhân. Giá trị của \(a\) bằng bao nhiêu?
A. \( - 4.\)
B. \(2.\)
C. \(4.\)
D. \( - 2.\)
Câu 16. Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } \left( {4 + {u_n}} \right) = 1.\) Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\) bằng
A. \( - 3.\)
B. 1.
C. \(4.\)
D. \( - 4.\)
Câu 17. \(\mathop {\lim }\limits_{n \to + \infty } \frac{{n + 1}}{{3n}}\) bằng
A. 1.
B. \( + \infty .\)
C. \( - \infty .\)
D. \(\frac{1}{3}.\)
Câu 18. Cho hàm số \(f\left( x \right)\) và \(g\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 4\) và \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = - 1.\) Giá trị \[\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - g\left( x \right)} \right]\] bằng
A. 5.
B. 3.
C. \( - \frac{1}{4}.\)
D. 0.
Câu 19. Kết quả của giới hạn \[\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 15}}{{x - 2}}\] là
A. \(0\).
B. \(1\).
C. \( + \infty .\)
D. \( - \infty .\)
Câu 20. Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
A. \(y = \sqrt x .\)
B. \(y = \cot x.\)
C. \(y = \tan x.\)
D. \(y = \frac{1}{{{x^2} + 1}}.\)
Câu 21. Cho hàm số \[f\left( x \right) = \frac{{x - 2}}{{\left| {x - 2} \right|}}.\] Hàm số \(f\left( x \right)\) liên tục trên
A. \(\left( { - \infty ; + \infty } \right).\)
B. \(\left[ {2; + \infty } \right).\)
C. \(\left( { - \infty ;2} \right].\)
D. \(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right).\)
Câu 22. Giá trị của \(a\) để hàm số \[f\left( x \right) = \left\{ \begin{array}{l}3x - 1\,\,\,\,\,{\rm{khi}}\,\,x \ne 1\\a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x \ne 1\end{array} \right.\] liên tục tại \(x = 1\) là
A. \(1.\)
B. \( - 1.\)
C. \(0.\)
D. \(2.\)
Câu 23. Yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt.
B. Hai đường thẳng cắt nhau.
C. Bốn điểm phân biệt.
D. Một điểm và một đường thẳng.
Câu 24. Cho hình chóp \(S.ABCD,\) gọi \(O\) là giao điểm của hai đường chéo \(BD\) và \(AC.\) Phát biểu nào dưới đây đúng?
A. Đường thẳng \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {ABCD} \right).\)
B. Đường thẳng \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right).\)
C. Đường thẳng \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBD} \right).\)
D. Đường thẳng \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right).\)
Câu 25. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong không gian, qua một điểm và một đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
B. Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
C. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy.
D. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đôi một song song.
Câu 26. Cho tứ diện \(ABCD.\) Gọi \(M,\,\,N\) lần lượt là các điểm thuộc các cạnh \(AB,\,\,AC\) sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); \(I,\,\,J\) lần lượt là trung điểm của \(BD\) và \(CD.\)
Khẳng định nào sau đây đúng?
A. \(IJ\) cắt \(BC.\)
B. \(IJ\) song song \(MN.\)
C. \(IJ\) và \(MN\) là hai đường thẳng chéo nhau.
D. \(IJ\) và \(MN\) là hai đường thẳng song song hoặc chéo nhau.
Câu 27. Cho đường thẳng \(d\) song song với mặt phẳng \(\left( P \right).\) Mệnh đề nào sau đây là đúng?
A. Đường thẳng \(d\) không có điểm chung với mặt phẳng \(\left( P \right).\)
B. Đường thẳng \(d\) có đúng một điểm chung với mặt phẳng \(\left( P \right).\)
C. Đường thẳng \(d\) có đúng hai điểm chung với mặt phẳng \(\left( P \right).\)
D. Đường thẳng \(d\) có vô số điểm chung với mặt phẳng \(\left( P \right).\)
Câu 28. Cho tứ diện \(ABCD\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC,\,\,CD.\) Đường thẳng \(BD\) song song với mặt phẳng nào dưới đây?
A. \(\left( {AMN} \right).\)
B. \(\left( {ABC} \right).\)
C. \(\left( {ABD} \right).\)
D. \(\left( {CMN} \right).\)
Câu 29. Cho tứ diện \(ABCD.\) Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác \(ABD\) và \[ACD.\] Đường thẳng \({G_1}{G_2}\) song song với mặt phẳng nào dưới đây?
A. \(\left( {ABC} \right).\)
B. \(\left( {ABD} \right).\)
C. \(\left( {ACD} \right).\)
D. \(\left( {A{G_1}{G_2}} \right).\)
Câu 30. Cho mặt phẳng \(\left( R \right)\) cắt hai mặt phẳng song song \(\left( P \right)\) và \[\left( Q \right)\] theo hai giao tuyến \(a\) và \(b.\) Mệnh đề nào sau đây đúng?
A. \(a\) và \(b\) có một điểm chung duy nhất.
B. \(a\) và \(b\) song song.
C. \(a\) và \(b\) trùng nhau.
D. \(a\) và \(b\) song song hoặc trùng nhau.
Câu 31. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O.\) Gọi \(M,\,\,N,\,\,P\) theo thứ tự lần lượt là trung điểm của \(SA,\,\,SB,\,\,SD.\) Khẳng định nào sau đây đúng?
A. \(\left( {MNP} \right){\rm{//}}\left( {ABCD} \right).\)
B. \(\left( {MNP} \right){\rm{//}}\left( {SCD} \right).\)
C. \(\left( {MNP} \right){\rm{//}}\left( {SBC} \right).\)
D. \(\left( {MNP} \right){\rm{//}}\left( {SAB} \right).\)
Câu 32. Số đường chéo trong một hình hộp là:
A. 2.
B. 4.
C. 24.
D. 28.
Câu 33. Cho hình hộp \(ABCD.A'B'C'D'\) có \(AC\) cắt \(BD\) tại \(O\) và \(A'C'\) cắt \(B'D'\) tại \(O'.\) Khi đó \(\left( {AB'D'} \right)\) song song với mặt phẳng nào dưới đây?
A. \(\left( {A'OC'} \right).\)
B. \(\left( {BDA'} \right).\)
C. \(\left( {BDC'} \right).\)
D. \(\left( {BCD} \right).\)
Câu 34. Cho các đường thẳng không song song với phương chiếu. Khẳng định nào sau đây là đúng?
A. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
B. Phép chiếu song song có thể biến hai đường thẳng song song thành hai đường thẳng cắt nhau.
C. Phép chiếu song song có thể biến hai đường thẳng song song thành hai đường thẳng chéo nhau.
D. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song
song hoặc trùng nhau.
Câu 35. Phép chiếu song song biến \(\Delta ABC\) thành \(\Delta A'B'C'\) theo thứ tự đó. Vậy phép chiếu song song nói trên, sẽ biến trung điểm \(M\) của cạnh \(BC\) thành
A. Trung điểm \(M'\) của cạnh \(B'C'.\)
B. Trung điểm \(M'\) của cạnh \(A'C'.\)
C. Trung điểm \(M'\) của cạnh \(A'B'.\)
D. Trung điểm \(M'\) của cạnh \(BC.\)
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{3n - 1}}{{2n + 3}}\); b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 4} - 2}}{x}.\]
Bài 2. (1 điểm) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Trên cạnh \(SC\) và \(AB\) lần lượt lấy hai điểm \(I\) và \(J\) sao cho \(CI = \frac{2}{3}SC\) và \(BJ = \frac{2}{3}AB.\)
a) Tìm giao điểm của đường thẳng \(SD\) và mặt phẳng \(\left( {ABI} \right).\)
b) Chứng minh rằng \(IJ{\rm{//}}\left( {SAD} \right).\)
Bài 3. (1 điểm) Một người chơi nhảy bungee trên một cây cầu với một sợi dây dài 100 m. Sau mỗi lần rơi xuống, người chơi được kéo lên một quãng đường có độ dài bằng \(80\% \) so với lần rơi trước và lại rơi xuống đúng bằng quãng đường vừa được kéo lên. Tính tổng quãng đường đi lên của người đó sau 10 lần được kéo lên.
–––––HẾT–––––
C. Đáp án và hướng dẫn giải đề kiểm tra cuối học kì 1
I. Bảng đáp án trắc nghiệm
|
1. D |
2. B |
3. B |
4. C |
5. D |
6. C |
7. A |
|
8. A |
9. D |
10. C |
11. D |
12. A |
13. D |
14. C |
|
15. D |
16. A |
17. D |
18. A |
19. D |
20. D |
21. D |
|
22. D |
23. B |
24. B |
25. B |
26. B |
27. A |
28. A |
|
29. A |
30. B |
31. A |
32. B |
33. C |
34. D |
35. A |
II. Hướng dẫn giải tự luận
Bài 1. (1 điểm)
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{3n - 1}}{{2n + 3}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{n\left( {3 - \frac{1}{n}} \right)}}{{n\left( {2 + \frac{3}{n}} \right)}}\) \( = \mathop {\lim }\limits_{n \to + \infty } \frac{{3 - \frac{1}{n}}}{{2 + \frac{3}{n}}} = \frac{3}{2}\).
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 4} - 2}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {\sqrt {{x^2} + 4} - 2} \right).\left( {\sqrt {{x^2} + 4} + 2} \right)}}{{x\left( {\sqrt {{x^2} + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} + 4 - 4}}{{x\left( {\sqrt {{x^2} + 4} + 2} \right)}}\]
\( = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2}}}{{x\left( {\sqrt {{x^2} + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{x}{{\sqrt {{x^2} + 4} + 2}} = \frac{0}{{\sqrt {0 + 4} + 2}} = 0.\)
Bài 2. (1 điểm)
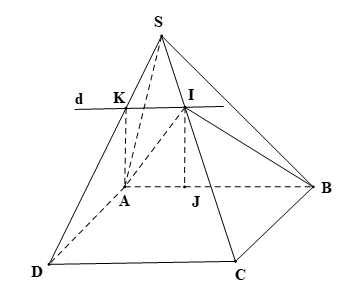
a) Ta có: \(I \in SC\) mà \(SC \subset \left( {SCD} \right) \Rightarrow I \in \left( {SCD} \right).\)
Mà \(I \in \left( {ABI} \right).\)
\( \Rightarrow I \in \left( {ABI} \right) \cap \left( {SCD} \right).\)
Hơn nữa: \(AB{\rm{//}}CD;\) \(AB \subset \left( {ABI} \right)\) và \(CD \subset \left( {SCD} \right).\)
\( \Rightarrow d = \left( {ABI} \right) \cap \left( {SCD} \right)\) sao cho \(d\) đi qua \(I\) và song song với \(AB,\,CD.\)
Trong \(\left( {SCD} \right)\) gọi \(K = d \cap SD.\)
Khi đó \(K \in d\) mà \[d \subset \left( {ABI} \right).\]
\( \Rightarrow K = SD \cap \left( {ABI} \right).\)
b) Ta có: \(CI = \frac{2}{3}SC \Rightarrow SI = \frac{1}{3}SC \Rightarrow \frac{{SI}}{{SC}} = \frac{1}{3};\)
\(BJ = \frac{2}{3}AB \Rightarrow AJ = \frac{1}{3}AB \Rightarrow \frac{{AJ}}{{AB}} = \frac{1}{3}.\)
\( \Rightarrow \frac{{SI}}{{SC}} = \frac{{AJ}}{{AB}} = \frac{1}{3}.\)
Lại có: \(KI{\rm{//}}CD\) (do \(d{\rm{//}}CD\)) nên theo hệ quả định lí Thalés có:
\(\frac{{KI}}{{CD}} = \frac{{SI}}{{SC}} \Rightarrow \frac{{KI}}{{CD}} = \frac{{AJ}}{{AB}}.\)
Mặt khác \(CD = AB\) (do \(ABCD\) là hình bình hành).
\( \Rightarrow KI = AJ.\)
Mà \(KI{\rm{//}}AJ\) (do \(d{\rm{//AB}}\))
Suy ra \(AKIJ\) là hình bình hành.
\( \Rightarrow IJ{\rm{//}}AK.\)
Hơn nữa: \(AK \subset \left( {SAD} \right)\) và \(IJ \not\subset \left( {SAD} \right).\)
Từ đó ta có \(IJ{\rm{//}}\left( {SAD} \right).\)
Bài 3. (1 điểm)
Gọi \({u_n}\) là quãng đường đi lên của người đó sau \(n\) lần kéo lên \(\left( {n \in {\mathbb{N}^*}} \right).\)
Sau lần kéo lên đầu tiên quãng đường đi lên của người đó là:
\({u_1} = 100.80\% = 100.0,8 = 80\) (m).
Sau lần kéo lên thứ hai quãng đường đi lên của người đó là:
\({u_2} = 80.80\% = 80.0,8\) (m).
Sau lần kéo lên thứ ba quãng đường đi lên của người đó là:
\({u_3} = 80.0,8.80\% = 80.0,8.0,8 = 80.0,{8^2}\) (m).
Khi đó, dãy số \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = 80\) và công bội \(q = 0,8.\)
Ta có công thức tổng quát \({u_n} = 80.{\left( {0,8} \right)^{n - 1}}\) (m).
Tổng quãng đường người đó đi được sau 10 lần kéo lên là:
\({S_{10}} = \frac{{80\left( {1 - 0,{8^{10}}} \right)}}{{1 - 0,8}} \approx 357,05\,\,\left( {\rm{m}} \right).\)
–––––HẾT–––––
Đề thi học kì 1 Toán 11 Cánh diều có đáp án - Đề 2
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 2)
I. Trắc nghiệm (7 điểm)
Câu 1. Trên đường tròn lượng giác, gọi là điểm biểu diễn cho góc lượng giác có số đo . Mệnh đề nào đúng trong các mệnh đề sau?
A. .
B. .
C. .
D. .
Câu 2. Chọn mệnh đề đúng trong các mệnh đề sau.
A. .
B. .
C. .
D. .
Câu 3. Trong các mệnh đề sau, mệnh đề nào sai?
A. .
B. .
C. .
D. .
Câu 4. Cho . Giá trị của biểu thức P = sin 2x.cos x bằng
A. .
B. .
C. .
D. .
Câu 5. Tập xác định của hàm số là
A. .
B. .
C. .
D. .
Câu 6. Hàm số nào sau đây là một hàm số chẵn?
A. .
B. .
C. .
D. .
Câu 7. Công thức nghiệm của phương trình là
A. .
B. .
C. .
D. .
Câu 8. Nghiệm của phương trình là
A. .
B. .
C. .
D. .
Câu 9. Với những giá trị nào của m thì phương trình có nghiệm?
A. .
B. .
C. .
D. .
Câu 10. Dãy số nào sau đây là dãy số tăng?
A. -1; 0; 3; 8; 16.
B. 1; 4; 16; 9; 25.
C. 0; 3; 8; 24; 15.
D. 0; 3; 12; 9; 6.
Câu 11. Cho dãy số , biết với . Số hạng thứ 3 của dãy số đó là:
A. 4.
B. 6.
C. 3.
D. 5.
Câu 12. Cho cấp số cộng với và . Công sai của cấp số cộng đã cho bằng
A. 4.
B. -4.
C. 6.
D. Không xác định.
Câu 13. Cho tam giác ABC có số đo của ba góc lập thành cấp số cộng và số đo góc nhỏ nhất bằng 30°. Góc có số đo lớn nhất trong ba góc của tam giác này là
A. 120°.
B. 90°.
C. 60°.
D. 100°.
Câu 14. Cho cấp số nhân có các số hạng lần lượt là 2; 4; 8; 16;... Số hạng tổng quát của cấp số nhân đó là
A. .
B. .
C. .
D. .
Câu 15. Cho cấp số nhân có số hạng đầu và công bội . Số hạng thứ 10 của cấp số nhân là
A. .
B. .
C. .
D. .
Câu 16. Cho hai dãy và thỏa mãn và . Giá trị của bằng
A. -1.
B. 1.
C. .
D. .
Câu 17. Biết với a là tham số. Khi đó bằng
A. -4.
B. -6.
C. -2.
D. 0.
Câu 18. Cho hàm số f(x) và g(x) thỏa mãn và . Giá trị bằng
A. .
B. 2.
C. 7.
D. 0.
Câu 19. Kết quả của giới hạn là
A. 0.
B. .
C. 1.
D. .
Câu 20. Hàm số y = f(x) có đồ thị như hình dưới đây:
Hàm số gián đoạn tại điểm
A. x = 1.
B. x = 3.
C. x = 0.
D. x = 2.
Câu 21. Cho các hàm số , và . Hàm số nào liên tục trên ℝ?
A. .
B. .
C. .
D. .
Câu 22. Tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục trên đoạn [a; b] và thì phương trình f(x) = 0 có nghiệm.
II. f(x) không liên tục trên [a; b] và thì phương trình f(x) = 0 vô nghiệm.
A. Chỉ I đúng.
B. Chỉ II đúng.
C. Cả I và II đúng.
D. Cả I và II sai.
Câu 23. Cho hình chóp tứ giác S.ABCD. Gọi O là giao điểm của AC và BD. Trong các mặt phẳng sau, điểm O không nằm trên mặt phẳng nào?
A. .
B. .
C. .
D. .
Câu 24. Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
C. Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Câu 25. Cho tứ diện ABCD vị trí tương đối của hai đường thẳng AC và BD là
A. Cắt nhau.
B. Song song.
C. Chéo nhau.
D. Trùng nhau.
Câu 26. Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và ABD. Khẳng định nào sau đây đúng?
A. IJ cắt AB.
B. IJ song song AB.
C. IJ và CD là hai đường thẳng chéo nhau.
D. IJ song song CD.
Câu 27. Cho đường thẳng a và mặt phẳng (P) không có điểm chung. Kết luận nào sau đây đúng?
A. a cắt (P).
B. a cắt (P) hoặc a chéo (P).
C. .
D. a chứa trong (P).
Câu 28. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Khẳng định nào sau đây sai?
A. .
B. .
C. .
D. .
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với mặt phẳng nào sau đây?
A. (ABCD).
B. (SAB).
C. (SCD).
D. (SBD).
Câu 30. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai mặt phẳng phân biệt không cắt nhau thì song song.
B. Qua một điểm nằm ngoài một mặt phẳng cho trước có vô số mặt phẳng song song với mặt phẳng đã cho.
C. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau.
D. Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, SD, AB. Khẳng định nào sau đây đúng?
A. .
B. .
C. .
D. .
Câu 32. Hình lăng trụ có đáy là hình bình hành được gọi là
A. Hình lăng trụ tam giác.
B. Hình hộp chữ nhật.
C. Hình hộp.
D. Hình lập phương.
Câu 33. Cho hình lăng trụ . Trong các khẳng định sau, khẳng định nào sai?
A. .
B. .
C. .
D. là hình chữ nhật.
Câu 34. Có bao nhiêu hình biểu diễn cho hình tứ diện trong bốn hình dưới đây?
A. 1.
B. 2.
C. 3.
D. 4.
Câu 35. Phép chiếu song song biến ba đường thẳng song song thành
A. Ba đường thẳng đôi một song song với nhau.
B. Một đường thẳng.
C. Hai đường thẳng song song.
D. Cả ba phương án A, B, C.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Tính các giới hạn sau:
a) .
b) .
Bài 2. (1 điểm) Cho hình lăng trụ tam giác . Gọi M, N lần lượt là trung điểm của và AB.
a) Chứng minh .
b) Mặt phẳng (P) đi qua N song song với hai cạnh và . Tìm giao tuyến của hai mặt phẳng (P) và .
Bài 3. (1 điểm)Cho hình vuông (C1) có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông (C2) (xem hình vẽ). Từ hình vuông (C2) lại tiếp tục làm như trên ta nhận được dãy các hình vuông . Gọi là diện tích của hình vuông . Đặt . Biết , tính a.
–––––HẾT–––––
ĐÁP ÁN
I. Bảng đáp án trắc nghiệm
|
1. A |
2. A |
3. C |
4. A |
5. A |
6. C |
7. B |
|
8. A |
9. D |
10. A |
11. A |
12. B |
13. B |
14. C |
|
15. A |
16. A |
17. B |
18. A |
19. A |
20. A |
21. B |
|
22. A |
23. B |
24. A |
25. C |
26. D |
27. C |
28. D |
|
29. A |
30. B |
31. B |
32. C |
33. D |
34. C |
35. D |
II. Hướng dẫn giải tự luận
Bài 1. (1 điểm) Tính các giới hạn sau:
a) .
b) .
Hướng dẫn giải
Bài 2. (1 điểm) Cho hình lăng trụ tam giác . Gọi M, N lần lượt là trung điểm của và AB.
a) Chứng minh .
b) Mặt phẳng (P) đi qua N song song với hai cạnh và . Tìm giao tuyến của hai mặt phẳng (P) và .
Hướng dẫn giải
a)
b)
Trong mặt phẳng , kẻ đường thẳng qua N song song với , cắt tại E.
Trong mặt phẳng , kẻ đường thẳng qua N song song với , cắt tại Q.
Khi đó, mặt phẳng (P) chính là mặt phẳng (NQE).
Vì nên ; vì nên . Do đó, .
Vậy hay .
Bài 3. (1 điểm)Cho hình vuông (C1) có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông (C2) (xem hình vẽ). Từ hình vuông (C2) lại tiếp tục làm như trên ta nhận được dãy các hình vuông . Gọi là diện tích của hình vuông . Đặt . Biết , tính a.
Hướng dẫn giải
Hình vuông đầu tiên (C1) có cạnh bằng a và diện tích là S1 = a2.
Lý luận tương tự ta có tạo thành một dãy cấp số nhân và công bội .
Vì nên là một cấp số nhân lùi vô hạn với và công bội .
Tổng của cấp số nhân lùi vô hạn này là
.
Mà nên . Suy ra a = 2 (do độ dài cạnh là số dương).
–––––HẾT–––––
Đề thi học kì 1 Toán 11 Cánh diều có đáp án - Đề 3
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 3)
Câu 1 : Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
Câu 2 : Chọn câu đúng
Câu 3 : Khi biểu diễn trên đường tròn lượng giác, góc lượng giác nào trong các góc lượng giác dưới đây có cùng điểm cuối, cùng điểm đầu với góc lượng giác có số đo .
Câu 4 : Nếu thì thuộc góc phần tư nào?
Câu 5 : Chọn đáp án đúng:
Câu 6 : Cấp số cộng với công sai d được cho bởi hệ thức:
Câu 7 : Dãy số gồm các số khác 0 thỏa mãn tỉ số không đổi thì dãy số là:
Câu 8 : Cho dãy số với . Tính .
Câu 9 : khi và chỉ khi:
Câu 10 : Cho hàm số liên tục trên đoạn . Mệnh đề nào đúng?
Câu 12 : Nếu thì:
Câu 13 : Cho hình chóp S. ABCD có O là giao điểm của AC và BD. Gọi M, I lần lượt là trung điểm của BD, SD. Điểm nào dưới đây thuộc mặt phẳng (SOC)?
Câu 14 : Chọn đáp án sai.
Câu 15 : Với điều kiện nào dưới đây thì đường thẳng d song song với mặt phẳng (P)?
Câu 16 : Nếu đường thẳng d và mặt phẳng (P) có … điểm chung thì d cắt mặt phẳng (P).
Từ (cụm từ) thích hợp điền vào “…” để được câu đúng là:
Câu 17 : Hình chóp S. ABCD có bao nhiêu đỉnh?
Câu 18 : Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa a và cắt mặt phẳng (P) theo giao tuyến b. Kết luận nào sau đây đúng?
Câu 19 : Cho và . Chọn đáp án đúng.
Câu 20 : Rút gọn biểu thức
Câu 21 : Giá trị của biểu thức bằng:
Câu 22 : Cho cấp số cộng có và với , . Số hạng tổng quát của cấp số cộng đã cho là:
Câu 23 : Theo ước tính, kể từ lúc mới mua, cứ sau mỗi 200 lần sạc thì pin của điện thoại X sẽ giảm 4% so với chu kỳ 200 lần sạc trước đó. Hỏi sau 1 200 lần sạc thì pin của điện thoại X còn lại bao nhiêu phần trăm so với lúc mới mua? (làm tròn đến chữ số thập phân thứ hai)
Câu 24 : Cho dãy số với . Chọn khẳng định đúng:
Câu 25 : Tìm số thực a khác 0 sao cho
Câu 26 : Giới hạn bằng:
Câu 27 : Biểu diễn số thập phân vô hạn tuần hoàn 3,333… dưới dạng phân số ta được:
Câu 28 : Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của BC, I là giao điểm của AM và BD, là mặt phẳng qua A, M và song song với SD. Mặt phẳng cắt SB tại N. Tỉ số là:
Câu 29 : Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD, P là điểm thuộc SA. Giao tuyến của hai mặt phẳng (SAD) và (PMN) là đường thẳng:
Câu 30 : Cho tứ diện ABCD và điểm M thuộc miền trong tam giác ACD. Gọi I và J lần lượt là hai điểm trên cạnh BC và BD sao cho IJ sao cho IJ không song song với CD. Gọi H là giao điểm của IJ với CD, K là giao điểm của MH và AC. Giao tuyến của hai mặt phẳng (ACD) và (IJM) là:
Câu 1 : Tìm các giá trị của tham số a để .
Câu 2 : Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi M là trung điểm của SA. J, K lần lượt thuộc BC, AD sao cho . Chứng minh rằng SC//( MJK).
Câu 3 : Cho hàm số . Chứng minh rằng
Câu 4 : Cho dãy số . Tìm số hạng tổng quát của dãy số trên.
ĐÁP ÁN
I. Bảng đáp án trắc nghiệm
| 1. A | 2. B | 3. C | 4. B | 5. A | 6. D |
| 7. B | 8. B | 9. A | 10. D | 11. A | 12. C |
| 13. A | 14. A | 15. C | 16. A | 17. B | 18. D |
| 19. C | 20. B | 21. D | 22. B | 23. A | 24. A |
| 25. D | 26. B | 27. A | 28. C | 29. B | 30. D |
Câu 1 :
Ta có:
Để thì
Câu 2 :
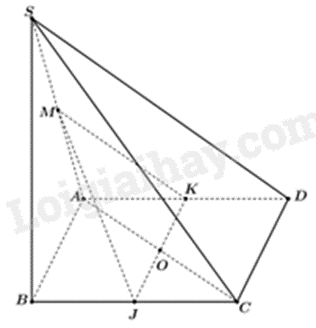
Vì và nên ,
Gọi O là giao điểm của AC và JK.
Tam giác JOC có JC//AK nên: , suy ra O là trung điểm của AC.
Vì M, O lần lượt là trung điểm của SA và AC nên MO là đường trung bình của tam giác SAC.
Do đó, MO//SC, mà nên SC//(MJK).
Câu 3 :
Gọi là một giá trị của hàm số. Khi đó, phương trình có nghiệm.
Ta có: (1)
Phương trình (1) có nghiệm
Vậy .
Câu 4 :
Với mọi ta có:
Đặt với mọi
Do đó, là một cấp số nhân với số hạng đầu và công bội
Số hạng tổng quát của là:
Vậy số hạng tổng quát của dãy số đã cho là: