Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 11 sách Cánh diều năm 2024 - 2025. Tài liệu gồm 10 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 11. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 11 Cánh diều bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi giữa kì 1 Toán 11 Cánh diều có đáp án năm 2024
Đề thi giữa kì 1 Toán 11 Cánh diều có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 1)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Nếu một góc lượng giác có số đo là thì số đo radian của nó là
A. ;
B. ;
C. ;
D. .
Câu 2. Điểm cuối của góc lượng giác ở góc phần tư thứ mấy nếu cùng dấu?
A. Thứ II;
B. Thứ IV;
C. Thứ II hoặc IV;
D. Thứ I hoặc III.
Câu 3. Cho góc lượng giác có số đo là . Số đo của các góc lượng giác nào sau đây có cùng tia đầu là và tia cuối là ?
A. ;
B. ;
C. ;
D. .
Câu 4. Cho . Khi đó bằng
A. ;
B. ;
C. ;
D. .
Câu 5. Cho góc thỏa mãn . Giá trị của là
A. ;
B. ;
C. ;
D. .
Câu 6. Rút gọn biểu thức ta được
A. ;
B. ;
C. ;
D.
Câu 7. Khẳng định nào sau đây là sai?
A. Hàm số là hàm số lẻ;
B. Hàm số là hàm số lẻ;
C. Hàm số là hàm số lẻ;
D. Hàm số là hàm số lẻ.
Câu 8. Hàm số có tập xác định là hàm số tuần hoàn nếu tồn tại một số khác 0sao cho ta có và
A. ;
B. ;
C. ;
D. .
Câu 9. Cho hàm số có đồ thị như hình vẽ dưới đây:
Hàm số nghịch biến trên khoảng nào?
A. ;
B. ;
C. ;
D. .
Câu 10. Tập xác định Dcủa hàm số là
A. ;
B. ;
C. ;
D. .
Câu 11. Giá trị lớn nhất của hàm số là
A. M = 3;
B. M = 2;
C. M = 1;
D. M = 0.
Câu 12. Công thức nghiệm với là công thức nghiệm của phương trình nào sau đây?
A. ;
B. ;
C. ;
D.
Câu 13. Nghiệm đặc biệt nào sau đây là sai?
A. ;
B. ;
C. ;
D. .
Câu 14. Các giá trị của tham số mđể phương trình vô nghiệm là
A. ;
B. ;
C. ;
D..
Câu 15. Nghiệm của phương trình là
A. ;
B. ;
C. ;
D. .
Câu 16. Với , cho dãy số có số hạng tổng quát . Năm số hạng đầu tiên của dãy số này là
A. ;
B. ;
C. ;
D. .
Câu 17. Với , cho dãy số gồm các số nguyên dương chia hết cho 7 là 7,14, 21, … Công thức số hạng tổng quát của dãy số này là
A. ;
B. ;
C. ;
D. .
Câu 18. Cho dãy số biết . Dãy số bị chặn trên bởi số nào dưới đây?
A. 0;
B. ;
C. ;
D. 1.
Câu 19. Cho cấp số cộng có số hạng đầu bằng và công sai bằng Công thức số hạng tổng quát là
A. ;
B. ;
C. ;
D. .
Câu 20. Cho dãy số là cấp số cộng với
A. số hạng đầu tiên là và công sai là ;
B. số hạng đầu tiên là và công sai là ;
C. số hạng đầu tiên là 0 và công sai là ;
D. số hạng đầu tiên là 0 và công sai là .
Câu 21. Tổng của bao nhiêu số hạng đầu của cấp số cộng bằng ?
A. 98;
B. 99;
C. 100;
D. 101.
Câu 22. Cho hai đường thẳng avà chéo nhau. Có bao nhiêu mặt phẳng chứa avà song song với ?
A. 0;
B. 1;
C. 2;
D. vô số.
Câu 23. Cho hình chóp (hình vẽ). Gọi O là giao điểm của AC và BD. Điểm Okhông thuộc mặt phẳng nào sau đây?
A. ;
B. ;
C. ;
D. .
Câu 24. Hình chóp lục giác có bao nhiêu mặt bên?
A. 4;
B. 5;
C. 6;
D. 7.
Câu 25. Khẳng định nào sau đây là đúng về hình tứ diện đều?
A. Mặt đáy là hình thoi;
B. Mặt đáy là hình vuông;
C. Mặt bên là tam giác cân;
D. Mặt bên luôn là tam giác đều.
Câu 26. Cho hình chóp A.BCD có là trọng tâm tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là
A. AN với N là trung điểm của CD;
B. AM với Mlà trung điểm của AB;
C. AH với Hlà hình chiếu của B trên CD;
D. AK với là hình chiếu của C trên .
Câu 27. Cho tứ diện ABCD có M, lần lượt là trung điểm của BC, . Gọi Glà trọng tâm của tam giác BCD. Gọi Ilà giao điểm của NGvới mặt phẳng (ABC). Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D.
Câu 28. Cho ba mặt phẳng phân biệt có , , . Khi đó ba đường thẳng sẽ
A. đôi một cắt nhau;
B. đôi một song song;
C. đồng quy;
D. đôi một song song hoặc đồng quy.
Câu 29. Trong không gian, cho ba đường thẳng biết và a, c chéo nhau. Khi đó hai đường thẳng b và csẽ
A. trùng nhau hoặc chéo nhau;
B. cắt nhau hoặc chéo nhau;
C. chéo nhau hoặc song song;
D. song song hoặc trùng nhau.
Câu 30. Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Khẳng định nào sau đây là đúng?
A. IJ song song với CD;
B. IJ song song với AB;
C. IJ chéo CD;
D. IJ cắt AB.
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là CD. Gọi M là trung điểm của SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây đúng?
A. MN và SD cắt nhau;
B. MN // CD;
C. MN và SC cắt nhau;
D. MN và CD chéo nhau.
Câu 32. Cho đường thẳng asong song với mặt phẳng . Nếu mặt phẳng chứa a và cắt theo giao tuyến b thì b và a là hai đường thẳng
A. cắt nhau;
B. trùng nhau;
C. chéo nhau;
D. song song với nhau.
Câu 33. Cho các giả thiết sau. Giả thiết nào kết luận đường thẳng asong song với mặt phẳng ?
A. a // b và ;
B. a // b và ;
C. a // b và ;
D. .
Câu 34. ABCD. Gọi M, N lần lượt là trung điểm của AB và AC. Đường thẳng MN song song với mặt phẳng
A. (ACD);
B. (ABD);
C. (BCD);
D. (ABC).
Câu 35. Cho tứ diện ABCD có G là trọng tâm của tam giác ABD, Q thuộc cạnh AB sao cho AQ = 2QB, P là trung điểm của AB. Khi đó
A. MN // (BCD);
B. GQ // (BCD);
C. MN cắt (BCD);
D. Q thuộc mặt phẳng (CDP).
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Giải các phương trình lượng giác:
a) ;b) .
Bài 2. (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thang (hai đáy AB > CD). Gọi M, N lần lượt là trung điểm của SA, SB.
a) Tìm giao điểm P của SC và mp (ADN).
b) Biết AN cắt DP tại I. Chứng minh SI // AB. Tứ giác SABI là hình gì?
Bài 3. (1,0 điểm) Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình , với t là thời gian tính bằng giây và x là quãng đường tính bằng cm. Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
-----HẾT-----
ĐÁP ÁN ĐỀ SỐ 01
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
Đáp án |
|
Câu |
Đáp án |
|
Câu |
Đáp án |
|
Câu |
Đáp án |
|
Câu 1 |
B |
|
Câu 11 |
C |
|
Câu 21 |
C |
|
Câu 31 |
B |
|
Câu 2 |
D |
|
Câu 12 |
D |
|
Câu 22 |
B |
|
Câu 32 |
D |
|
Câu 3 |
D |
|
Câu 13 |
A |
|
Câu 23 |
C |
|
Câu 33 |
D |
|
Câu 4 |
C |
|
Câu 14 |
A |
|
Câu 24 |
C |
|
Câu 34 |
C |
|
Câu 5 |
B |
|
Câu 15 |
D |
|
Câu 25 |
D |
|
Câu 35 |
B |
|
Câu 6 |
B |
|
Câu 16 |
C |
|
Câu 26 |
A |
|
|
|
|
Câu 7 |
B |
|
Câu 17 |
C |
|
Câu 27 |
A |
|
|
|
|
Câu 8 |
A |
|
Câu 18 |
D |
|
Câu 28 |
D |
|
|
|
|
Câu 9 |
B |
|
Câu 19 |
B |
|
Câu 29 |
B |
|
|
|
|
Câu 10 |
C |
|
Câu 20 |
B |
|
Câu 30 |
A |
|
|
|
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm)
a)
b)
Bài 2. (1,0 điểm)
a) Gọi
Khi đó nên .
b) HS tự chứng minh SI // AB // CD. Tứ giác SABI là hình bình hành.
Bài 3. (1,0 điểm)
Trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng 20 lần.
Đề thi giữa kì 1 Toán 11 Cánh diều có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 2)
Phần trắc nghiệm (5 điểm)
Câu 1: Giá trị biểu thức là:
|
A. |
B. |
|
C. |
D. |
Câu 2: Cho . Chọn đáp án đúng.
|
A. |
B. |
|
C. |
D. |
Câu 3: Chọn khẳng định đúng:
|
A. |
B. |
|
C. |
D. Cả A, B, C đều sai. |
Câu 4: Chọn đáp án đúng.
A. Hàm số với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại 1 số T khác 0 sao cho thì và
B. Hàm số với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại 1 số T khác 0 sao cho thì và
C. Hàm số với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại 1 số T khác 0 sao cho thì và
D. Hàm số với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại 1 số T khác 0 sao cho thì và
Câu 5: Nhiệt độ ngoài trời T (tính bằng oC) vào thời điểm t giờ trong một ngày ở thành phố X được cho bởi hàm số . Để bảo quản các tác phẩm nghệ thuật, hệ thống điều hòa của một bảo tàng tự động bật khi nhiệt độ ngoài trời từ 24oC trở lên. Dựa vào đồ thị của hàm số sin, xác định khoảng thời gian t trong ngày hệ thống điều hòa được bật.
|
A. 12 giờ đến 20 giờ |
B. 11 giờ đến 20 giờ |
|
C. 11 giờ đến 19 giờ |
D. 12 giờ đến 19 giờ |
Câu 6: Sử dụng máy tính cầm tay để giải phương trình với kết quả là radian (làm tròn kết quả đến hàng phần trăm) là:
|
A. |
B. |
|
C. Cả A và B đều đúng |
D. Cả A và B đều sai |
Câu 7: Phương trình có nghiệm khi:
|
A. |
B. |
|
C. |
D. |
Câu 8:
|
Một chồng cột gỗ được xếp thành các hàng, hai hàng liên tiếp hơn kém nhau 1 cột gỗ (hình bên). Gọi là số cột gỗ nằm ở hàng thứ n tính từ trên xuống và cho biết hàng trên cùng có 14 cột gỗ. Công thức số hạng tổng quát của dãy số là: |
 |
|
A. |
B. |
|
C. |
D. |
Câu 9: Cho dãy số với . Với giá trị nào của a thì là dãy số giảm?
|
A. |
B. |
|
C. |
D. |
Câu 10: Trong các dãy số sau, dãy nào là cấp số cộng với công sai âm?
|
A. |
B. |
|
C. |
D. Cả A, B, C đều sai |
Câu 11: Một cấp số cộng có số hạng thứ tám là 75 và số hạng thứ hai mươi là 39. Công thức tổng quát của cấp số cộng là:
|
A. |
B. |
|
C. |
D. |
Câu 12:

Một bức tường trang trí có dạng hình thang, rộng 4,8m ở đáy và rộng 2,4m ở đỉnh (hình vẽ bên). Các viên gạch hình vuông có kích thước phải được đặt sao cho mỗi hàng ở phía trên chứa ít hơn một viên so với hàng ở ngay phía dưới nó. Hỏi sẽ cần bao nhiêu viên gạch hình vuông như vậy để ốp hết bức tường?
|
A. 232 viên gạch |
B. 233 viên gạch |
|
C. 234 viên gạch |
D. 235 viên gạch |
Câu 13: Dãy số nào sau đây là dãy số tăng?
|
A. |
B. |
|
C. |
D. |
Câu 14: Cho hình chóp S. ABCD, khi đó mặt đáy của hình chóp là:
|
A. SAB |
B. SAC |
|
C. SBC |
D. ABCD |
Câu 15: Cho hai đường thẳng m, n cắt nhau và không đi qua điểm P. Xác định được nhiều nhất bao nhiêu mặt phẳng bởi m, n và P?
|
A. 1 mặt phẳng |
B. 2 mặt phẳng |
|
C. 3 mặt phẳng |
D. 4 mặt phẳng |
Câu 16: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SC. Giao điểm I của đường thẳng AM và mặt phẳng (SBD) là:
|
A. Trọng tâm tam giác SAC |
B. Trọng tâm của tam giác SBD |
|
C. Trực tâm tam giác SAC |
D. Trung điểm của SO |
Câu 17: Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
|
A. 1 |
B. 2 |
|
C. 3 |
D. 4 |
Câu 18: Cho hình bình hành ABCD và một điểm S không nằm trong mặt phẳng (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng nào sau đây?
|
A. AD |
B. AB |
|
C. AC |
D. BC |
Câu 19: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, CD. Gọi d là giao tuyến của hai mặt phẳng (SAD) và mặt phẳng (SBC). Trong các đường thẳng AD, MN, CB, AC, BD, đường thẳng d song song với bao nhiêu đường thẳng?
|
A. 1 |
B. 2 |
|
C. 3 |
D. 4 |
Câu 20: Để tích lũy tiền cho việc học đại học của con gái, cô H quyết định hằng tháng bỏ ra 600 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô H sẽ tích lũy được bao nhiêu tiền vào thời điểm gửi khoản tiền thứ 185?
|
A. 180,9275 triệu đồng |
B. 182,9275 triệu đồng |
|
C. 185,9275 triệu đồng |
D. 181,9275 triệu đồng |
Phần tự luận (5 điểm)
Bài 1. (1,5 điểm)
1) Giải các phương trình sau:
a)
b)
2) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3) Giải phương trình: Giải phương trình
Bài 2. (1,5 điểm)
a) Vào năm 2020, dân số của một thành phố là khoảng 1,4 triệu người. Giả sử mỗi năm, dân số của thành phố này tăng thêm khoảng 40 nghìn người. Hãy ước tính dân số của thành phố này vào năm 2030.
b) Một công ty dược phẩm đang thử nghiệm một loại thuốc mới. Một thí nghiệm bắt đầu với vi khuẩn. Một liều thuốc được sử dụng sau mỗi bốn giờ có thể tiêu diệt được vi khuẩn. Giữa các liều thuốc, số lượng vi khuẩn có thể tăng lên 25%. Viết công thức truy hồi cho lượng vi khuẩn sống trước mỗi lần sử dụng.
Bài 3. (1,0 điểm) Cho hình chóp S. ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD. Tìm giao tuyến của mặt phẳng (ABM) và mặt phẳng (SAC).
Bài 4. (1,0 điểm)
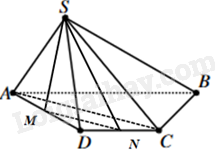
a) Cho hình chóp S. ABCD có đáy là hình thang, đáy lớn AB. Các điểm M, N lần lượt là trung điểm của AD, CD. Tìm giao tuyến của mặt phẳng (SAC) và mặt phẳng (SMN).
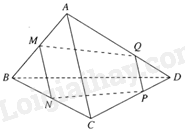
b) Cho tứ diện ABCD. Gọi M, N theo thứ tự là trung điểm của AB, BC và Q là một điểm nằm trên cạnh AD và P là giao điểm của CD với mặt phẳng (MNQ). Chứng minh rằng PQ//CA.
-------- Hết --------
ĐÁP ÁN
Phần trắc nghiệm (5 điểm)
|
Câu 1: B |
Câu 2: A |
Câu 3: C |
Câu 4: D |
Câu 5: A |
|
Câu 6: C |
Câu 7: D |
Câu 8: C |
Câu 9: B |
Câu 10: A |
|
Câu 11: D |
Câu 12: C |
Câu 13: A |
Câu 14: D |
Câu 15: C |
|
Câu 16: A |
Câu 17: C |
Câu 18: B |
Câu 19: C |
Câu 20: D |
Câu 1:
Đáp án B
Câu 2:
Mà
Nên
Đáp án A
Câu 3:
Ta có
Đáp án C
Câu 4:
Hàm số với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại 1 số T khác 0 sao cho thì và
Đáp án D
Câu 5:
Ta có: nên hay
Vì nên .
Xét đồ thị hàm số trên đoạn :
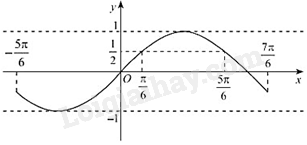
Ta thấy hay
Vậy hệ thống điều hòa được bật trong khoảng thời gian từ 12 giờ đến 20 giờ trong ngày.
Đáp án A
Câu 6:
Ta có:
Sau khi chuyển máy tính sang chế độ “radian”. Bấm liên tiếp
|
SHIFT |
sin |
0 |
. |
6 |
= |
Ta được kết quả gần đúng là 0,64.
Vậy phương trình có nghiệm là ;
Đáp án C
Câu 7:
Phương trình (1) có nghiệm khi và chỉ khi
Đáp án D
Câu 8:
Ta có:
Khi đó, số hạng tổng quát của dãy số là .
Đáp án C
Câu 9:
Ta có:
Xét:
Để là dãy số giảm thì với mọi , tức là với mọi
Mà với mọi nên
Vậy là dãy số giảm khi
Đáp án B
Câu 10:
Xét dãy số: , ta có:
Do đó, dãy số là cấp số cộng với công sai
Đáp án A
Câu 11:
Ta có:
Vậy số hạng tổng quát là:
Đáp án D
Câu 12:
Đổi
Số viên gạch ở hàng đầu tiên (ứng với đáy lớn là) (viên)
Số gạch ở hàng trên cùng (ứng với đáy nhỏ) là: (viên)
Vì mỗi hàng ở phía trên chứa ít hơn một viên so với hàng ở ngay phía dưới nó nên ta thu được cấp số cộng có công sai
Như vậy,
Vậy số viên gạch hình vuông cần thiết để ốp hết bức tường đó là:
(viên gạch)
Đáp án C
Câu 13:
Vì nên dãy số là dãy số tăng.
Đáp án A
Câu 14:
Hình chóp S. ABCD có mặt đáy là ABCD
Đáp án D
Câu 15:
Ta xác định được các mặt phẳng là: mặt phẳng (m, n), mặt phẳng (S, m), mặt phẳng (S, n). Vậy tạo được nhiều nhất ba mặt phẳng bởi m, n và P.
Đáp án C
Câu 16:
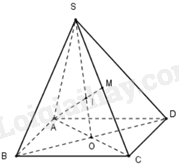
Trong mặt phẳng (SAC): Gọi I là giao điểm của AM và SO.
Mà nên I là giao điểm của AM và mặt phẳng (SBD).
Vì ABCD là hình bình hành nên O là trung điểm của AC.
Tam giác SAC có hai đường trung tuyến SO và AM cắt nhau tại I. Khi đó, I là trọng tâm của tam giác SAC
Đáp án A
Câu 17:
Hai đường thẳng phân biệt có ba vị trí tương đối là: song song, cắt nhau, chéo nhau.
Đáp án C
Câu 18:
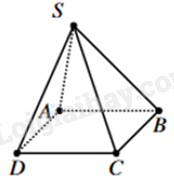
Vì ABCD là hình bình hành nên AB//CD
Mà và S thuộc cả hai mặt phẳng (SAB) và (SCD) nên giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song đi qua S và song song với AB.
Đáp án B
Câu 19:
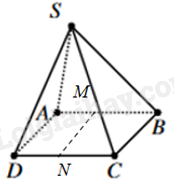
Vì ABCD là hình bình hành nên AD//CB
Mà và S thuộc cả hai mặt phẳng (SAD) và (SCB) nên giao tuyến d của hai mặt phẳng (SAD) và (SCB) là một đường thẳng song song đi qua S và song song với AD, CB.
Lại có, M, N lần lượt là trung điểm của AB, CD trong hình bình hành ABCD nên MN//AD//BC. Suy ra: d// MN//AD//BC
Vậy đường thẳng d song song với 3 đường thẳng là: MN, AD, BC.
Đáp án C
Câu 20:
Gọi là số triệu đồng mà cô H có ở tài khoản tiết kiệm tích lũy gửi lần thứ n (vào đầu tháng thứ n). Kí hiệu triệu đồng,
Số tiền của cô H ở tài khoản tiết kiệm ở đầu tháng thứ 1 là: .
Số tiền của cô H ở tài khoản tiết kiệm ở đầu tháng thứ 2 là: .
Số tiền của cô H ở tài khoản tiết kiệm ở đầu tháng thứ 3 là:
.
Tương tự cho các tháng tiếp theo, suy ra số tiền cô H ở tài khoản tiết kiệm ở đầu tháng thứ n là:
Vào thời điểm gửi khoản tiền thứ 185, cô H sẽ tích lũy được: (triệu đồng)
Đáp án D
Phần tự luận (5 điểm)
Bài 1. (1,5 điểm)
1) a)
Vậy phương trình đã cho có họ nghiệm là
b)
Vậy phương trình đã cho có họ nghiệm là
2) Ta có:
Vì nên vì vậy với mọi .
Giá trị lớn nhất của hàm số là 1, đạt được khi
Và giá trị nhỏ nhất của hàm số là , đạt được khi
3) Điều kiện:
Đặt , điều kiện , khi đó , thay vào phương trình (1) ta có:
(thỏa mãn điều kiện)
Với thì
(tmđk)
Vậy phương trình đã cho có họ nghiệm là:
Bài 2. (1,5 điểm)
a) Ta có: 1,4 triệu người nghìn người
Dân số mỗi năm của thành phố từ năm 2020 đến năm 2030 lập thành một cấp số cộng gồm 11 số hạng, số hạng đầu , công sai nên số hạng tổng quát của cấp số cộng là:
Do đó, (nghìn người)
Vậy dân số của thành phố vào năm 2030 là 1,8 triệu người.
b) Gọi là số vi khuẩn tại thời điểm ban đầu và là số vi khuẩn trước lần dùng thuốc lần thứ n.
Do mỗi liều thuốc được sử dụng sau bốn giờ có thể tiêu diệt vi khuẩn và giữa các liều thuốc, số lượng vi khuẩn có thể tăng lên 25% nên ta có
Bài 3. (1,0 điểm)
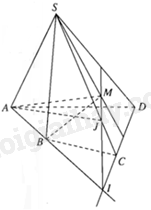
Trong mặt phẳng (ABCD), gọi I là giao điểm của AB và CD.
Vì
Trong mặt phẳng (SAC), gọi J là giao điểm của IM và SC.
Ta có:
Lại có: .
Do đó, giao tuyến của mặt phẳng (ABM) và mặt phẳng (SAC) là đường thẳng AJ.
Bài 4. (1,0 điểm)
|
a) Vì M, N lần lượt là trung điểm của AD, CD nên MN là đường trung bình của tam giác ACD. Do đó, AC//MN. Mà mặt phẳng (SAC) đi qua AC, mặt phẳng (SMN) đi qua MN và điểm S là điểm chung của mặt phẳng (SAC) và mặt phẳng (SMN). Do đó, giao tuyến của mặt phẳng (SAC) và mặt phẳng (SMN) là đường thẳng qua S song song với AC và MN. |
 |
|
b) Vì M, N theo thứ tự là trung điểm của AB, BC nên MN là đường trung bình của tam giác ABC. Do đó, MN//AC. Ba mặt phẳng (ABC), (ACD) và (MNQ) lần lượt cắt nhau theo các giao tuyến AC, MN và PQ. Mà MN//AC nên PQ//MN//AC |
 |