Tailieumoi.vn xin giới thiệu bộ đề thi học kì 2 môn Toán lớp 11 sách Chân trời sáng tạo năm 2024 – 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 2 Toán 11. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 11 Chân trời sáng tạo bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi học kì 2 Toán 11 Chân trời sáng tạo có đáp án năm 2025
Đề thi học kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 1
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 1)
I. Trắc nghiệm (7 điểm)
Câu 1. Biểu thức nào là luỹ thừa với số mũ thực
A. .
B. 2-x.
C. x-2.
D. 2x.
Câu 2. Cho a là số thực dương. Giá trị rút gọn của biểu thức là:
A. 2a.
B. a.
C. 1 - a.
D. 1 + a.
Câu 3. Cho hai số dương a, b với a ≠ 1. Số α thoả mãn aα = b, khi đó α bằng
A. .
B. .
C. .
D. .
Câu 4. Hàm số nào sau đây là hàm số mũ
A. .
B. y = -2x.
C. y = x-2.
D. y = x2.
Câu 5. Trong các hình sau, hình nào là dạng đồ thị của hàm số
A. (I).
B. (II).
C. (IV).
D. (III).
Câu 6. Một sinh viên gửi tiết kiệm ngân hàng lãi suất 13%/năm với hình thức lãi kép. Hỏi sau bao nhiêu năm sinh viên đó thu được gấp ba lần số tiền ban đầu, biết lãi suất cố định trong các năm.
A. 8 năm 9 tháng.
B. 15 năm 5 tháng.
C. 8 năm.
D. 9 năm.
Câu 7. Tổng các nghiệm thực của phương trình bằng
A. -7.
B. 5.
C. 6.
D. 7.
Câu 8. Tổng các giá trị nghiệm của phương trình bằng
A. 10.
B. .
C. 5.
D. .
Câu 9. Cho hàm số y = f(x) có đồ thị (C) và đạo hàm f'(2) = 6. Hệ số góc của tiếp tuyến của (C) tại điểm M(2;f(2)) bằng
A. 2.
B. 3.
C. 6.
D. 12.
Câu 10. Hàm số . Khi đó với thì khẳng định nào đúng ?
A. f'(a) = 2a + 3.
B. f'(a) = a2 + 1.
C. f'(a) = 2a + 2.
D. f'(a) = 2a.
Câu 11. Đạo hàm của hàm số y = 3x là
A. .
B. .
C. .
D. .
Câu 12. Một chất điểm chuyển động có phương trình s(t) = t + 1 (t tính bằng giây, s tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm t = 3s bằng
A. 1m/s.
B. 15m/s.
C. 4m/s.
D. 0m/s.
Câu 13. Hàm số y = x5 có đạo hàm cấp 2 là
A. 5x4.
B. 20x.
C. 20x3.
D. 5x3.
Câu 14. Cho f(x) = 201. Tính f''(x).
A. f''(x) = 2.
B. f''(x) = x.
C. f''(x) = 0.
D. f''(x) = 1.
Câu 15. Hàm số có đạo hàm cấp hai tại x = 1 là
A. .
B. .
C. .
D. .
Câu 16. Hàm số y = cot x có đạo hàm là:
A. .
B. .
C. .
D. .
Câu 17. Đạo hàm của hàm số y = 3x là
A. .
B. .
C. .
D. .
Câu 18. Cho . Biểu thức f'(1) có giá trị là bao nhiêu?
A. -1.
B. -2.
C. -12.
D. 1.
Câu 19. Đạo hàm của hàm số bằng biểu thức nào sau đây?
A. .
B. .
C. .
D. .
Câu 20. Tung một con xúc xắc, gọi A là biến cố: "Xuất hiện mặt có số chấm lớn hơn hoặc bằng 4", B là biến cố: " Xuất hiện mặt có số chấm nhỏ hơn hoặc bằng 2". Khẳng định nào sau đây là đúng?
A. A và B là hai biến cố xung khắc.
B. A và B là hai biến cố đối.
C. Cả A và B đều đúng.
D. Không đủ thông tin để kết luận.
Câu 21. Cho A, B là hai biến cố xung khắc. Biết P(A) = , P(B) = . Tính .
A. .
B. .
C. .
D. .
Câu 22. Hai xạ thủ M và N cùng bắn súng vào một tấm bia. Biết rằng xác suất bắn trúng của xạ thủ M là 0,3, của xạ thủ N là 0,2. Khả năng bắn trúng của hai xạ thủ là độc lập. Xác suất của biến cố "Cả hai xạ thủ đều bắn trúng" là
A. 0,05.
B. 0,06.
C. 0,07.
D. 0,08.
Câu 23. Gọi S là tập các số tự nhiên có 4 chữ số khác nhau được tạo từ tập E = {1;2;3;4;5}. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chẵn?
A. .
B. .
C. .
D. .
Câu 24. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi A là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và B là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố .
A. .
B. .
C. .
D. .
Câu 25. Cho A, B là hai biến cố độc lập. Biết P(A) = 0,5; P(A ∩ B) = 0,2. Tính .
A. 0,3.
B. 0,5.
C. 0,6.
D. 0,7.
Câu 26. Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng A'C' và BD bằng.
A. 60°.
B. 30°.
C. 45°.
D. 90°.
Câu 27. Cho hình lập phương ABCD.A'B'C'D' như hình vẽ
Khẳng định nào sau đây đúng
A. .
B. .
C. .
D. .
Câu 28. Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là:
A. Bh.
B. Bh.
C. Bh.
D. 3Bh.
Câu 29. Cho hình chóp S.ABCD có ABCD là hình chữ nhật và SA ⊥ (ABCD). Mệnh đề nào dưới đây đúng ?
A. AB ⊥ (SAD).
B. BC ⊥ (SAD).
C. AC ⊥ (SAD).
D. BD ⊥ (SAD).
Câu 30. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng và tam giác SAC đều. Thể tích của khối chóp đã cho bằng
A. .
B. .
C. .
D. .
Câu 31. Cho hai mặt phẳng (P) và (Q) cắt nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?
A. 1.
B. 2.
C. 3.
D. Vô số.
Câu 32. Cho hình chóp S.ABCD có ABCD là hình vuông, SA vuông góc với mặt phẳng đáy. Mặt phẳng (ABCD) vuông góc với mặt phẳng nào dưới đây ?
A. (SAC).
B. (SBD).
C. (SCD).
D. (SBC).
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD). Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
A. .
B. .
C. .
D. .
Câu 34. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) khi a và b song song (hoặc a trùng với b).
C. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
D. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì a song song với b.
Câu 35. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = 2a, tam giác ABC vuông tại B, AB = và BC = a (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng
A. 90°.
B. 45°.
C. 30°.
D. 60°.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) a) Tính đạo hàm cấp hai của hàm số y = sinax (a là hằng số).
b) Một chất điểm chuyển động có quãng đường được cho bởi phương trình , trong đó t > 0 với t tính bằng giây (s) và s tính bằng mét (m). Tính vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất.
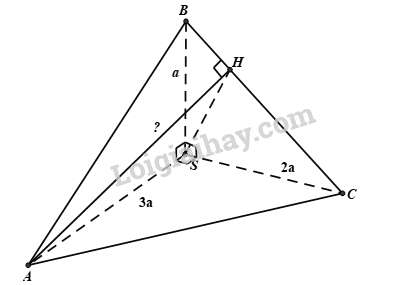
Bài 2. (1 điểm) Cho hình chóp S.ABCD có đáy là tam giác vuông cân tại A, SA ⊥ (ABC) và AB = a; SA = . Gọi H là trung điểm cạnh BC.
a) Chứng minh: BC ⊥ (SAH).
b) Tính góc giữa đường thẳng SH và mặt phẳng (ABC).
Bài 3. (1 điểm) Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc A. Tính xác suất để số tự nhiên được chọn chia hết cho 25.
-----HẾT-----
ĐÁP ÁN
I. Bảng đáp án trắc nghiệm
|
1. A |
2. D |
3. A |
4. A |
5. D |
6. D |
7. D |
|
8. D |
9. C |
10. C |
11. B |
12. A |
13. C |
14. C |
|
15. D |
16. B |
17. B |
18. B |
19. D |
20. A |
21. B |
|
22. B |
23. B |
24. C |
25. D |
26. D |
27. C |
28. B |
|
29. A |
30. C |
31. A |
32. A |
33. B |
34. B |
35. B |
II. Hướng dẫn giải tự luận
Bài 1. (1 điểm)
a)
.
b) Gọi v(t), a(t) lần lượt là vận tốc và gia tốc của chất điểm.
Ta có .
Mà với mọi t, dấu “=” xảy ra khi chỉ khi t = 1.
Suy ra gia tốc chuyển động của chất điểm nhỏ nhất bằng 2m/s2 khi t = 1.
Vận tốc chuyển động của chất điểm tại thời điểm gia tốc nhỏ nhất là
(m/s).
Bài 2. (1 điểm)
Bài 3. (1 điểm)
Số phần tử không gian mẫu .
Gọi A là biến cố chọn được số chia hết cho 25.
Đề thi học kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 2
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 11
Thời gian làm bài: phút
(Đề số 2)
Câu 1 : Tính giá trị của biểu thức :
Câu 2 : Trong các hình sau, hình nào là dạng đồ thị của hàm số
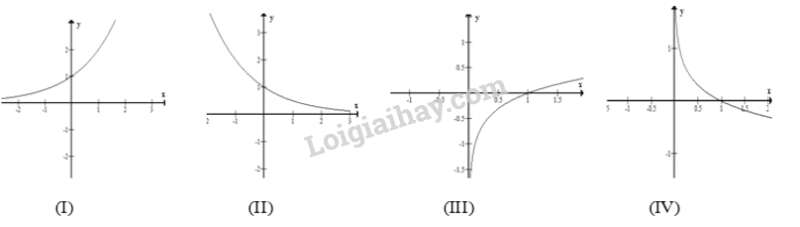
A.(I).
B.(II).
C.(IV).
D.(III).
Câu 3 : Cho hình chóp có Gọi lần lượt là trực tâm các tam giác và. Mệnh đề nào sai trong các mệnh đề sau?

đồng quy tại một điểm
Câu 4 : Cho tứ diện trong đó, , vuông góc với nhau từng đôi một và, ,. Khoảng cách từ đến đường thẳng bằng
Câu 5 : Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:
Câu 6 : Cho hàm số có đồ thị Phương trình tiếp tuyến của tại giao điểm của với trục tung là
Câu 7 : Cho hàm số . Khi đó đạo hàm y’ là
Câu 8 : Hàm số có đạo hàm . Khi đó có kết quả bằng
Câu 9 : Hàm số có đạo hàm . Khi đó có kết quả là:
Câu 10 : Một chất điểm chuyển động có phương trình ( tính bằng giây, tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm bằng
Câu 11 : Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng:
Câu 12 : Hàm số có đạo hàm là:
Một chất điểm chuyển động có phương trình chuyển động là (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số tại thời điểm là:
b) Tính vận tốc tức thời của chuyển động tại thời điểm là
c) Tính gia tốc tức thời của chuyển động tại thời điểm là
d) Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là t = 2 (s)
Cho hàm số có đồ thị (C):
a) Phương trình tiếp tuyến của (C) tại giao điểm của với trục Oy là:
b) Phương trình tiếp tuyến của (C) tại giao điểm của với trục Ox là là
c) Phương trình tiếp tuyến của (C) tại giao điểm của tại giao điểm của với đường thẳng là:
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến là và
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC. AH, IJ là đường cao tam giác AID.
a)
b)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là
Câu 1 : Tính giới hạn:
Câu 2 : Cho hàm số : . Tính .
Câu 3 : Cho hình chóp tứ giác đềucó tất cả các cạnh bằng . Tính khoảng cách từ đỉnh đến mặt phẳng
Câu 4 : Cho hình chóp có đáy là hình vuông cạnh .Cạnh bên vuông góc với mặt phẳng và .Góc giữa đường thẳng và mặt phẳng bằng
Câu 5 : Cho hàm số với . Biết rằng đồ thị hàm số đi qua hai điểm và , đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng có hệ số góc bằng 2. Tính tổng .
Câu 6 : Cho hàm số có đồ thị Tìm điểm trên đồ thị sao cho tiếp tuyến của tại tạo với hai trục tọa độ một tam giác có diện tích bằng