Với giải HĐ7 trang 62 Chuyên đề Toán 11 Kết nối tri thức chi tiết trong Bài 11: Hình chiếu vuông góc và hình chiếu trục đo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:

Giải Chuyên đề Toán 11 Bài 11: Hình chiếu vuông góc và hình chiếu trục đo

HĐ7 trang 62 Chuyên đề Toán 11: Cho hình tứ diện vuông OABC có các cạnh OA, OB, OC bằng nhau và lần lượt nằm trên các trục Ox, Oy, Oz đôi một vuông góc. Xét phép chiếu vuông góc lên mặt phẳng (P) đi qua O sao cho các trục Ox, Oy, Oz tạo với (P) các góc bằng nhau (H.3.23a). Gọi A', B', C' lần lượt là hình chiếu của A, B, C.

a) Chứng minh rằng ABC là tam giác đều.

b) Giải thích tại sao các khoảng cách từ A, B, C đến (P) bằng nhau, từ đó suy ra mặt phẳng (ABC) song song với mặt phẳng (P).

c) Gọi I là tâm tam giác đều ABC. Giải thích tại sao $\widehat{A\text{'}OB\text{'}}=\widehat{AIB}$ , từ đó suy ra $\widehat{A\text{'}O\text{'}B\text{'}}=\widehat{B\text{'}O\text{'}C\text{'}}=\widehat{A\text{'}O\text{'}C\text{'}}=120°$ .

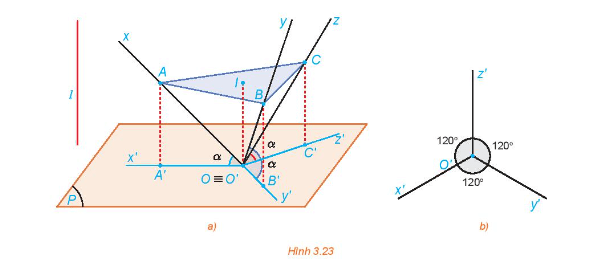
Lời giải:

a) Ta có: OA = OB = OC, $\widehat{AOB}=\widehat{BOC}=\widehat{COA}=90°$ .

Suy ra các tam giác AOB, BOC và COA bằng nhau từng đôi một.

Từ đó suy ra AB = BC = CA nên tam giác ABC là tam giác đều.

b) Ta có: OA = OB = OC;$\widehat{AA\text{'}O}=\widehat{BB\text{'}O}=\widehat{CC\text{'}O}=90°$ ; $\widehat{AOA\text{'}}=\widehat{BOB\text{'}}=\widehat{COC\text{'}}=\alpha$ .

Do đó, các tam giác AA'O, BB'O và CCO' bằng nhau từng đôi một.

Từ đó suy ra AA' = BB' = CC'.

Do đó, khoảng cách từ A, B, C đến (P) bằng nhau.

Ta có: AA' = BB', AA' // BB' nên ABB'A' là hình bình hành.

Suy ra: AB // A'B'.

Tương tự ta chứng minh BC // B'C'; CA // C'A'

Mà A'B', B'C', C'A' thuộc (P)

Suy ra: (ABC) song song với (P).

c) Dễ dàng chứng minh được IA = O'A' (AIO'A' là hình bình hành).

Tương tự IB = O'B', AB = A'B'.

Do đó ∆IAB = ∆O'A'B' (c.c.c).

Suy ra $\widehat{A\text{'}O\text{'}B\text{'}}=\widehat{AIB}$ .

Tương tự, ta chứng minh được $\widehat{A\text{'}O\text{'}C\text{'}}=\widehat{CIA};\widehat{B\text{'}O\text{'}C\text{'}}=\widehat{BIC}.$

Do I là tâm tam giác đều ABC nên dễ dàng chứng minh được $\widehat{AIB}=\widehat{BIC}=\widehat{CIA}=120°$ .

Nên suy ra $\widehat{AIB}=\widehat{BIC}=\widehat{CIA}=\widehat{A\text{'}O\text{'}B\text{'}}=\widehat{B\text{'}O\text{'}C\text{'}}=\widehat{A\text{'}O\text{'}C\text{'}}$ .

Vậy $\widehat{A\text{'}O\text{'}B\text{'}}=\widehat{B\text{'}O\text{'}C\text{'}}=\widehat{A\text{'}O\text{'}C\text{'}}=120°$ .