Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chùm toán hình học THCS, tài liệu bao gồm 157 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu gồm có:

I. Lý thuyết

II. Bài tập

CÁC CHÙM BÀI TẬP THƯỜNG GẶP

I. Chùm bài tập xuất phát từ ba đường cao của một tam giác:

Bài 1: Cho tam giác ABC nhọn nội tiếp đường tròn (O;R) cố định. Kẻ các đường thằn AD, BE, CF cắt nhau tại H. BE, CF cắt (O) tại điểm thứ hai lần lượt là M và N. Gọi I là trung điểm BC. Kẻ đường kính AK của (O).

1) Chứng minh các tứ giác BFEC, AFHE,… nội tiếp.

2)

2.1. Chứng minh tứ giác BHCK là hình bình hành.

2.2. Chứng minh DC.DB = DH.DA

2.3. Chứng minh AF.AB = AE.AC

2.4. Chứng minh H và M đối xừn nhau qua AC

2.5. Chứng minh EF//MN

2.6. Chứng minh AB.AC = 2R.AD

3)

3.1. Chứng minh EF = BC. cosBAC.

3.2. Chứng minh \(BH.BE + CH.CF = B{C^2}\)B

3.3 Chứng minh

\(\begin{array}{l}BH.BE + CH.CF + AH.AD\\ = \frac{1}{2}\left( {A{B^2} + B{C^2} + A{C^2}} \right)\end{array}\)

3.4 Chứng minh \(AO \bot EF\)

3.5 Gọi P và Q lần lượt là hình chiếu của D trên BH và CH. Chứng minh PQ//EF

3.6 Gỉa sử \(\widehat {BAC} = {45^o}\), \({S_{ABC}} = 100c{m^2}\). Tính diện tích \(\Delta AFE\).

3.7 Chứng minh H là tâm đường tròn nội tiếp tam giác EFD.

3.8 Chứng minh IF là tiếp tuyến của đường tròn ngoại tiếp tam giác HEF.

3.9 Tính tỉ số \(\frac{{OI}}{{AH}}\)

3.10 Qua A kẻ đường thẳng xy song song với EF. Chứng minh xy là tiếp tuyến của (O;R).

3.11 Gọi L là điểm đối xứng với K qua B. Chứng minh L thuộc đường tròn ngoại tiếp tam giác AHB.

3.12 Gọi S là điểm đối xứng với K qua C. Chứng minh H là trung điểm của LS.

3.13 Chứng minh FEID là tứ giác nối tiếp.

Hướng dẫn giải

   Bài 1:

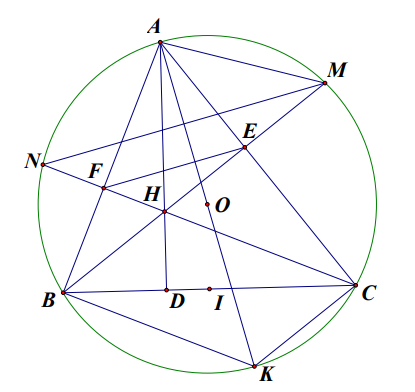
1) Xét tứ giác BFEC:  mà hai góc ở hai đỉnh kề nhau cùng nhìn cạnh BC

\( \Rightarrow \) tứ giác BFEC nội tiếp (dhnb)

Xét tứ giác BFHE: \(\widehat {AFH} + \widehat {AEH} = {90^o} + {90^o} = {180^o}\) mà hai góc ở hai đỉnh đối nhau

\( \Rightarrow \)tứ giác BFHE nội tiếp (dhnb)

2)

2.1. Xét (O): \(\widehat {ABK}\), \(\widehat {ACK}\) nội tiếp chắn cung AK, mà AK là đường kính

Vì \(\left. {\begin{array}{*{20}{c}}{BE \bot AC}\\{KC \bot AC}\end{array}} \right\} \Rightarrow BE//KC\)

Vì \(\left. {\begin{array}{*{20}{c}}{CF \bot AB}\\{BK \bot AB}\end{array}} \right\} \Rightarrow CF//BK\)

Xét tứ giác BHCK: \(\left. {\begin{array}{*{20}{c}}{BH//CK}\\{CH \bot BK}\end{array}} \right\} \Rightarrow \) tứ giác BHCK là hình bình hành (dhnb)

2.2. Có \(\widehat {ABD} + \widehat {BAD} = {90^o}\) và \(\widehat {ABD} + \widehat {HCD} = {90^o} \Rightarrow \widehat {BAD} = \widehat {HCD}\)

Xét \(\Delta ABD\) và \(\Delta CHD\)

\(\left. {\begin{array}{*{20}{c}}{\widehat {ABD} = \widehat {DHC}}\\{\widehat {ADB} = \widehat {CDH}\left( { = {{90}^o}} \right)}\end{array}} \right\} \Rightarrow \Delta ABD\)$~\Delta CHD$(g.g)

\( \Rightarrow \frac{{DB}}{{DA}} = \frac{{DH}}{{DC}} \Rightarrow DB.DC = DH.DA\)

2.3.

Xét \(\Delta AFC\) và \(\Delta AEB\)

\(\left. {\begin{array}{*{20}{c}}{\widehat {BAC}chung}\\{\widehat {AFC} = \widehat {AEB}\left( { = {{90}^o}} \right)}\end{array}} \right\} \Rightarrow \Delta AFC\)$~\Delta AEB$(g.g)

\( \Rightarrow \frac{{AF}}{{AC}} = \frac{{AE}}{{AB}} \Rightarrow AF.AB = AE.AC\)

2.4. Có \(\widehat {HBD} + \widehat {BHD} = {90^o}\)

và \(\widehat {HBD} + \widehat {ECB} = {90^o} \Rightarrow \widehat {BHD} = \widehat {ACB}\)

mà \(\widehat {BHD} = \widehat {AHE}\)(dd) \( \Rightarrow \widehat {AHE} = \widehat {ACB}\)

Xét (O): \(\widehat {AMH} = \widehat {ACB}\) (góc nội tiếp chắn cung AB) mà \(\widehat {AHE} = \widehat {ACB}\) (cmt)

\( \Rightarrow \widehat {AMH} = \widehat {AHM} \Rightarrow \Delta AHM\) cân tại A có \(AE \bot HM\)\( \Rightarrow AE\)là trung trực của HM hay H và M đối xứng với nhau qua E (dpcm)

2.5. Xét (O): \(\widehat {NMB} = \widehat {NCB}\) (góc nội tiếp chắn cung NB)

Xét tứ giác nội tiếp BFEC: \(\widehat {FCB} = \widehat {FEB}\) (góc nội tiếp chắn cung FB)

\( \Rightarrow \widehat {NME} = \widehat {FEB}\) mà hai góc ở vị trí đồng vị \( \Rightarrow MN//EF\) (dhnb)

2.6. Xét (O): \(\widehat {AKB} = \widehat {ACB}\) (góc nội tiếp chắn cung AB)

Xét \(\Delta AKB\) và \(\Delta ACD\)

\(\left. {\begin{array}{*{20}{c}}{\widehat {AKB} = \widehat {ACD}}\\{\widehat {ABK} = \widehat {ADC}\left( { = {{90}^o}} \right)}\end{array}} \right\} \Rightarrow \Delta AKB\)$~\Delta ACD$(g.g)\( \Rightarrow \frac{{AK}}{{AC}} = \frac{{AB}}{{AD}} \Rightarrow AK.AD = AB.AC \Rightarrow AB.AC = 2R.AD\)

3)

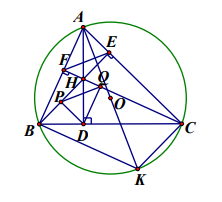
3.1 Do BFEC là tứ giác nội tiếp nên

\(\widehat {AEF} = \widehat {ABC}\) (cùng phụ với \(\widehat {FEC}\) )

Xét \(\Delta AEF\)và \(\Delta ABC\) có: \(\widehat {BAC}\) chung, \(\widehat {AEF} = \widehat {ABC}\)

\(\Delta AEF\)$\Delta ABC$ (g.g)

\( \Rightarrow \frac{{FE}}{{BC}} = \frac{{AF}}{{AC}} \Rightarrow EF = BC.\frac{{AF}}{{AC}}\)

Lại có \(\cos \widehat {BAC} = \frac{{AF}}{{AC}} \Rightarrow EF = BC.\cos \widehat {BAC}\)

3.2 Xét \(\Delta BEC\) và \(\Delta BDH\) có: \(\widehat B\) chung, \(\widehat {BEC} = \widehat {BDH} = {90^o}\)

\( \Rightarrow \Delta BEC\)$~\Delta BDH$(g.g)

\( \Rightarrow \frac{{BE}}{{BD}} = \frac{{BC}}{{BH}} \Rightarrow BH.BE = BD.BC\)

Chứng minh tương tự ta có: \(CH.CF = CD.BC\)

Suy ra: \(BH.BE + CH.CF = \left( {BD + CD} \right)BC = B{C^2}\)

3.3 Chứng minh tương tự ý 3.2 ta có: \(BH.BE + AH.AD = A{B^2}\); \(AH.AD + CH.CF = A{C^2}\)

Suy ra:

\(\begin{array}{l}2BH.BE + 2CH.CF + 2AH.AD\\ = B{C^2} + A{B^2} + A{C^2}\end{array}\)

Suy ra:

\(\begin{array}{l}BH.BE + CH.CF + AH.AD\\ = \frac{1}{2}\left( {A{B^2} + B{C^2} + A{C^2}} \right)\end{array}\)

3.4 Do AK là đường kính nên \(\widehat {ACK} = {90^o}\) (góc n)ội tiếp chắn nửa đường tròn)

\[ \Rightarrow \widehat {AKC} + \widehat {CAK} = {90^o}\] hay \(\widehat {AKC} + \widehat {EAO} = {90^o}\) (1)

Lại có \(\widehat {AKC} = \widehat {ABC}\) (hai góc nội tiếp cùng chắn một cung)

Mà \(\widehat {ABC} = \widehat {AEF}\) (ý b) \( \Rightarrow \widehat {AKC} = \widehat {AEF}\) (2)

Từ (1) và (2) \( \Rightarrow \widehat {AEF} + \widehat {EAO} = {90^o} \Rightarrow AO \bot EF\)

3.5 Do DPHQ là tứ giác nội tiếp (tổng hai góc đối bằng 180^o) nên

\(\widehat {HPQ} = \widehat {HDQ}\) (hai góc nội tiếp cùng chắn 1 cung)

Mà DQ//AB (cùng vuông góc với CF) \( \Rightarrow \widehat {FAH} = \widehat {HDQ}\)

Suy ra: \(\widehat {HPQ} = \widehat {FAH}\)

Lại có AEHF nội tiếp nên \(\widehat {FAH} = \widehat {FEH}\) (hai góc nội tiếp cùng chắn 1 cung)

Do đó: \(\widehat {HPQ} = \widehat {FEH}\)

Mà hai góc ở vị trí so le trong nên EF//PQ

3.6 Ta có: \(\Delta AEF\)$\Delta ABC$ (ý 3.1)

 \( \Rightarrow \frac{{{S_{AEF}}}}{{{S_{ABC}}}} = {\left( {\frac{{AE}}{{AB}}} \right)^2} = {\cos ^2}{45^o} = \frac{1}{2}\)

\( \Rightarrow {S_{AEF}} = \frac{1}{2}{S_{ABC}} = 50c{m^2}\)

3.7 Do \(\widehat {FAH} = \widehat {FEH}\)(cm ý 3.5)

Mà \(\widehat {FAH} = \widehat {HCD}\) (cùng phụ với \(\widehat {ABC}\)) (3)

Mặt khác CDHE nội tiếp (tổng hai góc đối bằng 90^o)

Nên \(\widehat {HED} = \widehat {HCD}\) (4) (hai góc nội tiếp cùng chắn 1 cung)

Từ (3), (4) \( \Rightarrow \widehat {FEH} = \widehat {HED}\)

\( \Rightarrow EH\) là phân giác của \(\widehat {FED}\)

Tương tự DH là phân giác của \(\widehat {FDE}\)

Xét \(\Delta DEF\) có H là giao điểm ba đường phân giác nên H là tâm đường tròn nội tiếp \(\Delta DEF\).