Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tổng hợp các đề ôn thi HSG Toán lớp 8 với lời giải chi tiết, tài liệu bao gồm 105 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu gồm có
I. Đề ôn thi.
ĐỀ SỐ 1
(Thời gian làm bài 150 phút)
Bài 1: (2 điểm)
a) Tính giá trị của biểu thức:
\(A = {2018^2} + {2016^2} + {2014^2} + ... + {4^2} + {2^2} - \left( {{{2017}^2} + {{2015}^2} + {{2013}^2} + ... + {3^2} + 1} \right)\).
b) Cho \(x + y + z = 0\) và \({x^2} + {y^2} + {z^2} = 4\). Tính giá trị của biểu thức \(B = {x^4} + {y^4} + {z^4}\).
Bài 2: (4 điểm)
1. Với n![]() N. Chứng minh rằng:
N. Chứng minh rằng:
a) \(C = {n^4} + 6{n^3} + 11{n^2} + 6n + 1\) là số chính phương.
b) \(D = {5^{n + 2}} + {26.5^n} + {8^{2n + 1}}\) chia hết cho 59.
2. Tìm n![]() N để \({n^5} + 1\) chia hết cho \({n^3} + 1\).
N để \({n^5} + 1\) chia hết cho \({n^3} + 1\).
Bài 3: (4 điểm)
a) Giải phương trình:
\(\begin{array}{l}\frac{{2009 - x}}{7} + \frac{{2007 - x}}{9} + \frac{{2005 - x}}{{11}} + \frac{{2003 - x}}{{13}}\\ = \frac{{x - 17}}{{ - 1999}} + \frac{{x - 15}}{{ - 2001}} + \frac{{x - 13}}{{ - 2003}} + \frac{{x - 11}}{{ - 2005}}\end{array}\).
b) Xác định m để phương trình \(\frac{{x + m}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) có nghiệm duy nhất.
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = \frac{{8x + 3}}{{4{x^2} + 1}}\).
d) Tìm giá trị của \(x\)để \(Q = 2019 - (x - 1)\left( {x + 2} \right)\left( {x + 3} \right)\left( {x + 6} \right)\) đạt giá trị lớn nhất.
Bài 4: (2 điểm)
Chứng minh rằng \(f\left( x \right) = \frac{{19{x^5}}}{5} + \frac{{8{x^3}}}{3} + \frac{{27{x^2}}}{2} - \frac{{29x}}{{30}}\) nhận giá trị nguyên khi x là số nguyên.
Bài 5: (4 điểm)
1. Cho tam giác ABC, ba đường phân giác AM, BN, CP đồng quy tại I.
Chứng minh rằng \(\frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = \frac{{IM}}{{AM}} + \frac{{IN}}{{BN}} + \frac{{IP}}{{CP}}\).
2. Cho tam giác ABC vuông tại A, đường phân giác BD. Qua D kẻ đường thẳng song song với AB cắt BC tại E. Gọi F là giao điểm của AE và BD.
a) Chứng minh rằng đường thẳng CF đi qua trung điểm của AB.
b) Tính độ dài đoạn thẳng DE, biết AD = 3cm, DC = 5cm.
Bài 6: (4 điểm)
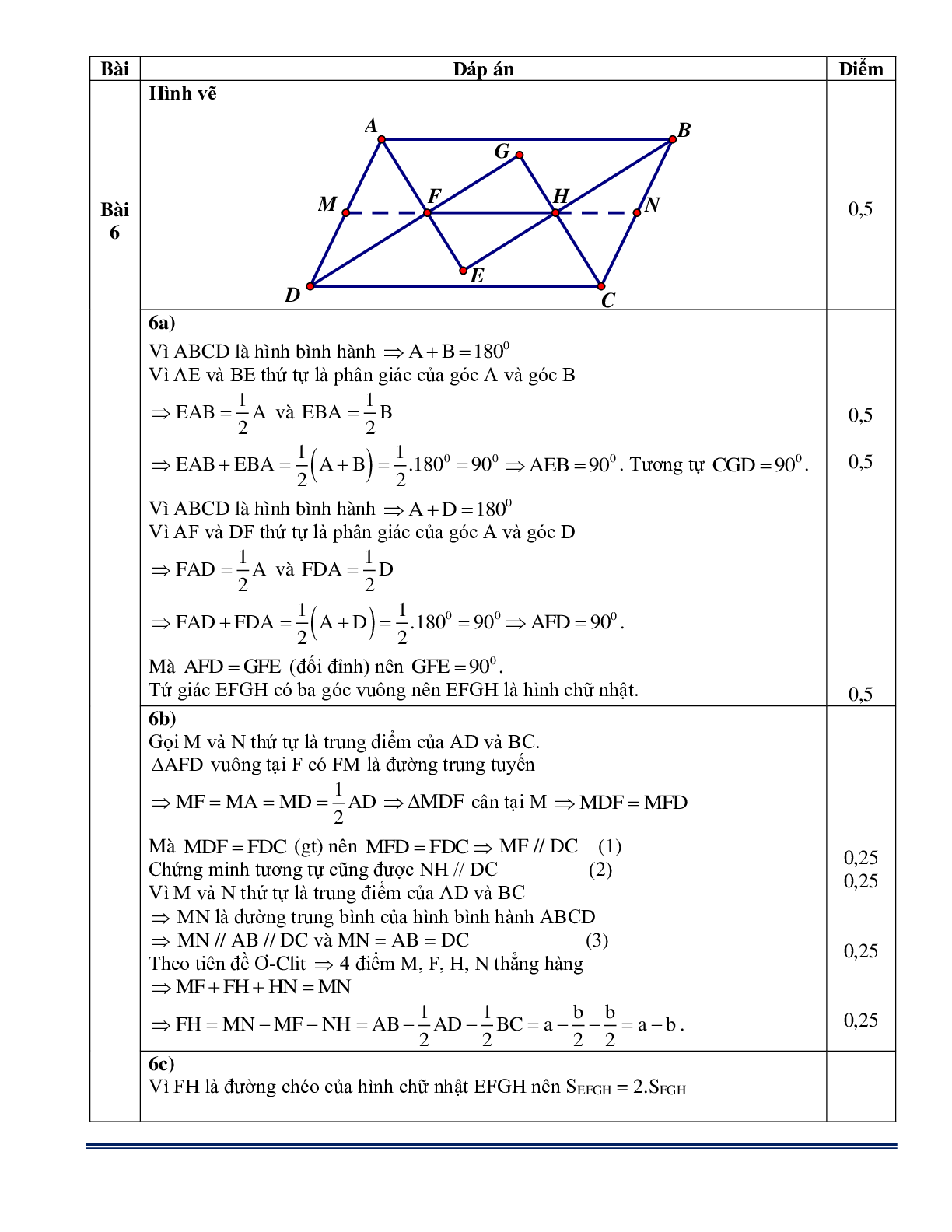
Cho hình bình hành ABCD. Tia phân giác góc A cắt các tia phân giác góc B và góc D thứ tự ở E và F; Tia phân giác góc C cắt các tia phân giác của góc B và góc D thứ tự ở H và G.
a) Chứng minh rằng tứ giác EFGH là hình chữ nhật.
b) Cho AB = a, BC = b (a>b). Tính HF theo a và b.
c. Hình bình hành ABCD cần thêm điều kiện gì để diện tích EFGH bằng \(\frac{{{{(a - b)}^2}}}{2}\).
ĐỀ SỐ 1
(Thời gian làm bài 150 phút)
HƯỚNG DẪN CHẤM
Bài 1: (2 điểm)
a) Tính giá trị của biểu thức:
\(A = {2018^2} + {2016^2} + {2014^2} + ... + {4^2} + {2^2} - \left( {{{2017}^2} + {{2015}^2} + {{2013}^2} + ... + {3^2} + 1} \right)\).
b) Cho \(x + y + z = 0\) và \({x^2} + {y^2} + {z^2} = 4\). Tính giá trị của biểu thức \(B = {x^4} + {y^4} + {z^4}\).
|
Bài |
Đáp án |
Điểm |
|
Bài 1 |
1a) \(A = {2018^2} + {2016^2} + {2014^2} + ... + {4^2} + {2^2} - \left( {{{2017}^2} + {{2015}^2} + {{2013}^2} + ... + {3^2} + 1} \right)\) \(A = \left( {{{2018}^2} - {{2017}^2}} \right) + \left( {{{2016}^2} - {{2015}^2}} \right) + \left( {{{2014}^2} - {{2013}^2}} \right) + ... + \left( {{2^2} - {1^2}} \right)\) \(A = 2018 + 2017 + 2016 + 2015 + 2014 + 2013 + ... + 2 + 1\) \(A = \frac{{2018\left( {2018 + 1} \right)}}{2} = 2037171\). |
|
|
1b) Ta có \(\begin{array}{l}x + y + z = 0 \Leftrightarrow {\left( {x + y + z} \right)^2} = 0\\ \Leftrightarrow {x^2} + {y^2} + {z^2} + 2\left( {xy + yz + zx} \right) = 0\end{array}\) Vì \({x^2} + {y^2} + {z^2} = 4\)nên \(4 + 2\left( {xy + yz + zx} \right) = 0 \Leftrightarrow xy + yz + zx = - 2\) \( \Rightarrow {\left( {xy + yz + zx} \right)^2} = 4 \Leftrightarrow {x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} + 2xyz\left( {x + y + z} \right) = 4\) Vì \(x + y + z = 0\) nên \({x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} = 4\). Ta có \(\begin{array}{l}{x^2} + {y^2} + {z^2} = 4 \Leftrightarrow \left( {{x^2} + {y^2} + {z^2}} \right) = 16\\ \Leftrightarrow {x^4} + {y^4} + {z^4} + 2\left( {{x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2}} \right) = 16\end{array}\) Mà \({x^2}{y^2} + {y^2}{z^2} + {z^2}{x^2} = 4\) nên \({x^4} + {y^4} + {z^4} = 8\). |
|
Bài 2: (4 điểm)
1. Với n![]() N. Chứng minh rằng:
N. Chứng minh rằng:
a) \(C = {n^4} + 6{n^3} + 11{n^2} + 6n + 1\) là số chính phương.
b) \(D = {5^{n + 2}} + {26.5^n} + {8^{2n + 1}}\) chia hết cho 59.
2. Tìm n![]() N để \({n^5} + 1\) chia hết cho \({n^3} + 1\).
N để \({n^5} + 1\) chia hết cho \({n^3} + 1\).
|
Bài |
Đáp án |
Điểm |
|
Bài 2 |
2.1a) Ta có \(C = {n^4} + 6{n^3} + 11{n^2} + 6n + 1\) \(C = {n^4} + 2{n^2}\left( {3n + 1} \right) + 9{n^2} + 6n + 1\) \(C = {n^4} + 2{n^2}\left( {3n + 1} \right) + {\left( {3n + 1} \right)^2}\) \(C = {\left( {{n^2} + 3n + 1} \right)^2}\) Vì n là số tự nhiên nên C là số chính phương. |
|
|
2.1b) \(\begin{array}{l}D = {5^{n + 2}} + {26.5^n} + {8^{2n + 1}} = {25.5^n} + {26.5^n} + {8.64^n}\\ = {51.5^n} + {64.8^n} = {59.5^n} + 8\left( {{{64}^n} - {5^n}} \right)\end{array}\) Vì \({64^n} - {5^n} \vdots 64 - 5 \vdots 59\) nên \(8\left( {{{64}^n} - {5^n}} \right) \vdots 59\) và \({59.5^n} \vdots 59\) với mọi số tự nhiên n. Do đó \(D = {5^{n + 2}} + {26.5^n} + {8^{2n + 1}}\) chia hết cho 59 với mọi số tự nhiên n. |
|
|
|
2.2 Ta có \({n^5} + 1 \vdots {n^3} + 1 \Rightarrow {n^2}\left( {{n^3} + 1} \right) - \left( {{n^5} + 1} \right) \vdots {n^3} + 1 \Rightarrow {n^2} - 1 \vdots {n^3} + 1\) \( \Rightarrow \left( {{n^3} + 1} \right) - n\left( {{n^2} - 1} \right) \vdots {n^3} + 1 \Rightarrow n + 1 \vdots {n^3} + 1 \Rightarrow 1 \vdots {n^2} - n + 1\) \( \Rightarrow \left[ {\begin{array}{*{20}{c}}{{n^2} - n + 1 = 1}\\{{n^2} - n + 1 = - 1}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{n \in \left\{ {0;1} \right\}}\\{n \in \emptyset }\end{array}} \right.\) Sau khi thử lại ta được \(n \in \left\{ {0;1} \right\}\) thì \({n^5} + 1\) chia hết cho \({n^3} + 1\). |
|
Bài 3: (4 điểm)
a) Giải phương trình:
\(\begin{array}{l}\frac{{2009 - x}}{7} + \frac{{2007 - x}}{9} + \frac{{2005 - x}}{{11}} + \frac{{2003 - x}}{{13}}\\ = \frac{{x - 17}}{{ - 1999}} + \frac{{x - 15}}{{ - 2001}} + \frac{{x - 13}}{{ - 2003}} + \frac{{x - 11}}{{ - 2005}}\end{array}\).
b) Xác định m để phương trình \(\frac{{x + m}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) có nghiệm duy nhất.
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = \frac{{8x + 3}}{{4{x^2} + 1}}\).
d) Tìm giá trị của \(x\)để \(Q = 2019 - (x - 1)\left( {x + 2} \right)\left( {x + 3} \right)\left( {x + 6} \right)\) đạt giá trị lớn nhất.
|
Bài |
Đáp án |
Điểm |
|
|
3a) \(VT + 4 = \frac{{2009 - x}}{7} + 1 + \frac{{2007 - x}}{9} + 1 + \frac{{2005 - x}}{{11}} + 1 + \frac{{2003 - x}}{{13}} + 1\) \(VT + 4 = \frac{{2016 - x}}{7} + \frac{{2016 - x}}{9} + \frac{{2016 - x}}{{11}} + \frac{{2016 - x}}{{13}}\) \(VP + 4 = \frac{{x - 17}}{{ - 1999}} + 1 + \frac{{x - 15}}{{ - 2001}} + 1 + \frac{{x - 13}}{{ - 2003}} + 1 + \frac{{x - 11}}{{ - 2005}} + 1\) \(VP + 1 = \frac{{x - 2016}}{{ - 1999}} + \frac{{x - 2016}}{{ - 2001}} + \frac{{x - 2016}}{{ - 2003}} + \frac{{x - 2016}}{{ - 2005}}\) Do đó \(\frac{{2016 - x}}{7} + \frac{{2016 - x}}{9} + \frac{{2016 - x}}{{11}} + \frac{{2016 - x}}{{13}} = \frac{{x - 2016}}{{ - 1999}} + \frac{{x - 2016}}{{ - 2001}} + \frac{{x - 2016}}{{ - 2003}} + \frac{{x - 2016}}{{ - 2005}}\) \( \Leftrightarrow \left( {2016 - x} \right)\left( {\frac{1}{7} + \frac{1}{9} + \frac{1}{{11}} + \frac{1}{{13}}} \right) = \left( {2016 - x} \right)\left( {\frac{1}{{1999}} + \frac{1}{{2001}} + \frac{1}{{2003}} + \frac{1}{{2005}}} \right)\) \( \Leftrightarrow 2016 - x = 0 \Leftrightarrow x = 2016\) |
|
|
|
3b) ĐKXĐ: \(x \ne - 1\);\(x \ne 0\). \(\frac{{x + m}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) (1) \( \Rightarrow \left( {m - 3} \right)x = 2\) (*) Phương trình (1) có nghiệm duy nhất \( \Leftrightarrow \)Phương trình (*) có nghiệm duy nhất khác -1 và 0. \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 3}\\{\frac{2}{{m - 3}}}\\{\frac{2}{{m - 3}} \ne 0}\end{array}} \right. \ne - 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 3}\\{2 \ne - m + 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 3}\\{m \ne 1}\end{array}} \right.\) Vậy khi \(\left\{ {\begin{array}{*{20}{c}}{m \ne 3}\\{m \ne 1}\end{array}} \right.\) thì phương trình (1) có nghiệm duy nhất. |
|
|
|
3c) ĐKXĐ: với mọi x thuộc R. \(P = \frac{{8x + 3}}{{4{x^2} + 1}} = \frac{{\left( {4{x^2} + 8x + 4} \right) - \left( {4{x^2} + 1} \right)}}{{4{x^2} + 1}} = \frac{{4{{\left( {x + 1} \right)}^2} - \left( {4{x^2} + 1} \right)}}{{4{x^2} + 1}} = \frac{{4{{\left( {x + 1} \right)}^2}}}{{4{x^2} + 1}} - 1 \ge - 1\) Dấu “=” xảy ra khi \(\frac{{4{{\left( {x + 1} \right)}^2}}}{{4{x^2} + 1}} = 0 \Leftrightarrow x = \frac{1}{4}\). Vậy GTLN của biểu thức P là 4, đạt được khi \(x = \frac{1}{4}\). |
|
|
|
3d) ĐKXĐ: với mọi x thuộc R. \(Q = 2019 - \left( {x - 1} \right)\left( {x + 2} \right)\left( {x + 3} \right)\left( {x + 6} \right)\) \(Q = 2019 - \left( {{x^2} + 5x - 6} \right)\left( {{x^2} + 5x + 6} \right)\) \(Q = 2019 - \left[ {{{\left( {{x^2} + 5x} \right)}^2} - 36} \right]\) \(Q = 2055 - {\left( {{x^2} + 5x} \right)^2} \le 2055\) Dấu “=” xảy ra khi \({x^2} + 5x = 0 \Leftrightarrow x = 0\) hoặc \(x = - 5\). Vậy khi \(x = 0\) hoặc \(x = - 5\) thì biểu thức Q đạt GTLN bằng 2055. |
|
Bài 4: (2 điểm)
Chứng minh rằng \(f\left( x \right) = \frac{{19{x^5}}}{5} + \frac{{8{x^3}}}{3} + \frac{{27{x^2}}}{2} - \frac{{29x}}{{30}}\) nhận giá trị nguyên khi x là số nguyên.
|
Bài |
Đáp án |
Điểm |
|
Bài 4 |
\(f\left( x \right) = \frac{{19{x^5}}}{5} + \frac{{8{x^3}}}{3} + \frac{{27{x^2}}}{2} - \frac{{29x}}{{30}} = \frac{{114{x^5} + 80{x^3} + 405{x^2} - 29x}}{{30}}\) f(x) nhận giá trị nguyên \( \Leftrightarrow 114{x^5} + 80{x^3} + 405{x^2} - 29x \vdots 30\) Ta có \(114{x^5} + 80{x^3} + 405{x^2} - 29x\) \( = \left( {120{x^5} + 90{x^3} + 390{x^2} - 30x} \right) - \left( {6{x^5} + 10{x^3} - 15{x^2} - x} \right)\) Do đó cần chứng minh \(6{x^5} + 10{x^3} - 15{x^2} - x \vdots 30\) Ta có \(6{x^5} + 10{x^3} - 15{x^2} - x = 6\left( {{x^5} - x} \right) + 10\left( {{x^3} - x} \right) - 15x\left( {x - 1} \right)\) Vì \({x^5} - x \vdots 30\); \({x^3} - x \vdots 30\) và \(x\left( {x - 1} \right) \vdots 30\) với mọi số nguyên x Do đó \(6{x^5} + 10{x^3} - 15{x^2} - x = 6\left( {{x^5} - x} \right) + 10\left( {{x^3} - x} \right) - 15x\left( {x - 1} \right) \vdots 30\). \( \Rightarrow f\left( x \right) = \frac{{19{x^5}}}{5} + \frac{{8{x^3}}}{3} + \frac{{27{x^2}}}{2} - \frac{{29x}}{{30}}\) nhận giá trị nguyên khi x là số nguyên. |
|
Bài 5: (4 điểm)
1. Cho tam giác ABC, ba đường phân giác AM, BN, CP đồng quy tại I.
Chứng minh rằng \(\frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = \frac{{IM}}{{AM}} + \frac{{IN}}{{BN}} + \frac{{IP}}{{CP}}\).
2. Cho tam giác ABC vuông tại A, đường phân giác BD. Qua D kẻ đường thẳng song song với AB cắt BC tại E. Gọi F là giao điểm của AE và BD.
a) Chứng minh rằng đường thẳng CF đi qua trung điểm của AB.
b) Tính độ dài đoạn thẳng DE, biết AD = 3cm, DC = 5cm.
|
Bài |
Đáp án |
Điểm |
|
|
Hình vẽ
|
|
|
|
5.1 Áp dụng tính chất đường phân giác của tam giác, ta có: \(\frac{{MB}}{{MC}} = \frac{{AB}}{{AC}}\); \(\frac{{NC}}{{NA}} = \frac{{BC}}{{BA}}\); \(\frac{{PA}}{{PB}} = \frac{{CA}}{{CB}}\) \( \Rightarrow \frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{BA}}.\frac{{CA}}{{CB}} = 1\) (1) Kẻ \(AH \bot BC\) và \(IK \bot BC\) (H và K thuộc BC) \( \Rightarrow AH\)// \(IK\) Áp dụng định lí Ta -lét ta có: \(\frac{{IM}}{{AM}} = \frac{{IK}}{{AH}}\) Ta lại có \(\frac{{{S_{IBC}}}}{{{S_{ABC}}}} = \frac{{IK}}{{AH}}\), do đó \(\frac{{IM}}{{AM}} = \frac{{{S_{IBC}}}}{{{S_{ABC}}}}\). Tương tự \(\frac{{IN}}{{BN}} = \frac{{{S_{IAC}}}}{{{S_{ABC}}}}\); \(\frac{{IP}}{{CP}} = \frac{{{S_{IAB}}}}{{{S_{ABC}}}}\). Vậy \(\frac{{IM}}{{AM}} + \frac{{IN}}{{BN}} + \frac{{IP}}{{CP}} = \frac{{{S_{IBC}}}}{{{S_{ABC}}}} + \frac{{{S_{IAC}}}}{{{S_{ABC}}}} + \frac{{{S_{IAB}}}}{{{S_{ABC}}}} = \frac{{{S_{ABC}}}}{{{S_{ABC}}}} = 1\) (2) Từ (1) và (2) \( \Rightarrow \frac{{MB}}{{MC}}.\frac{{NC}}{{NA}}.\frac{{PA}}{{PB}} = \frac{{IM}}{{AM}} + \frac{{IN}}{{BN}} + \frac{{IP}}{{CP}}\). |
|