Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Nâng cao và phát triển Toán 7 - tập 2, tài liệu bao gồm 122 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt tài liệu

Chương III: Thống kê

Chương IV: Biểu thức đại số

Phần đại số

Chương III: Thống kê

Tiết 11: Bảng “tần số” và biểu đồ

Khi nghiên cứu một hiện tượng tự nhiên hay xã hội, người ta thường tiến hành thống kê. Các số liệu thống kê thường được thể hiện bằng các giá trị số, chúng thường được viết thành một bảng (gọi tắt là bảng “tần số”).
Số lần xuất hiện của một giá trị trong bảng gọi là tần số của giá trị đó. Tỉ số giữa tần số của một giá trị và số tất cả các giá trị được thống kê là tần suất của giá trị đó.
Ví dụ 47
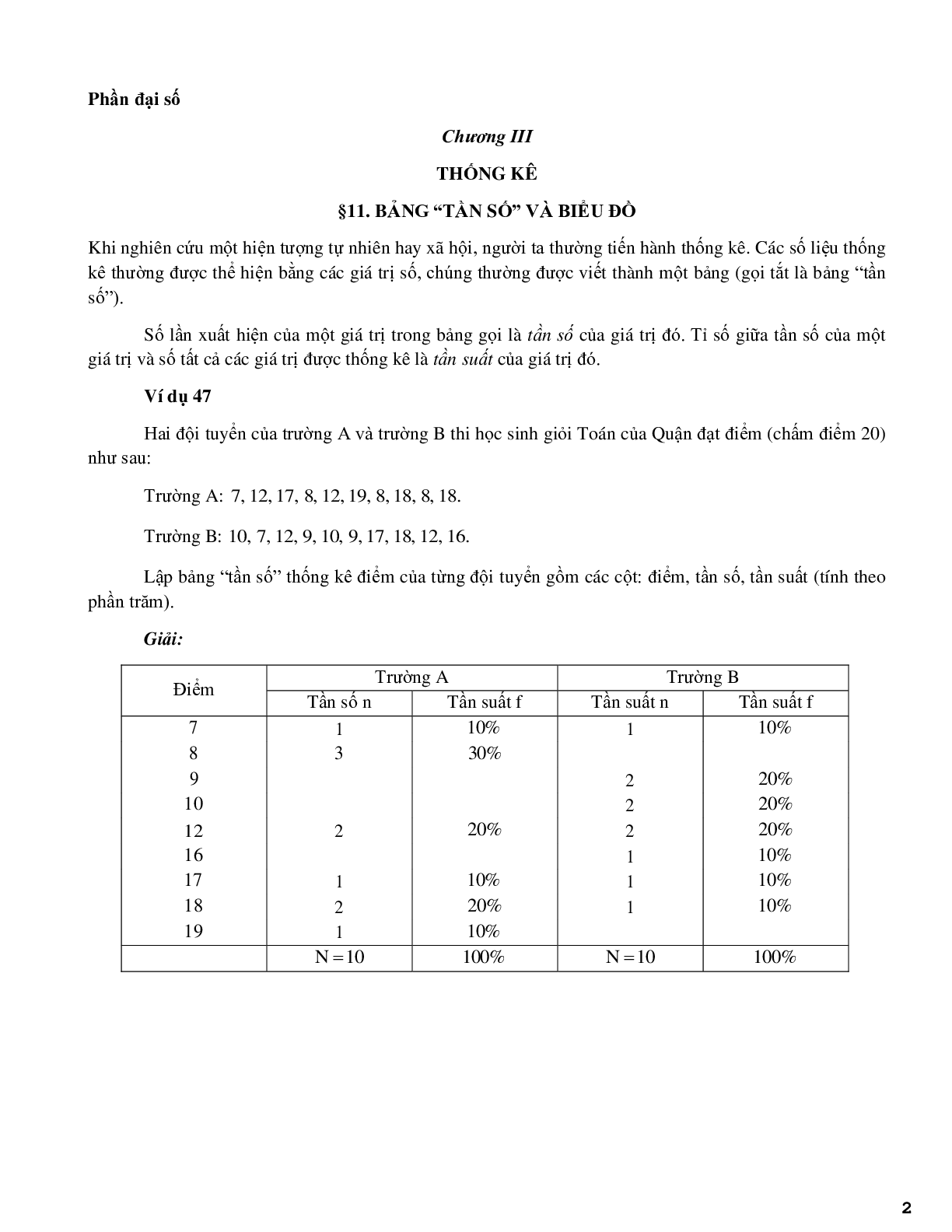
Hai đội tuyển của trường A và trường B thi học sinh giỏi Toán của Quận đạt điểm (chấm điểm 20) như sau:
Trường A: 7, 12, 17, 8, 12, 19, 8, 18, 8, 18.
Trường B: 10, 7, 12, 9, 10, 9, 17, 18, 12, 16.
Lập bảng “tần số” thống kê điểm của từng đội tuyển gồm các cột: điểm, tần số, tần suất (tính theo phần trăm).
Giải:

Bài tập

167. Bạn Tâm đếm các chữ cái trong dòng chữ “NGÀN HOA VIỆC TỐT DÂNG LÊN CÔ THẦY” để cắt khẩu hiệu. Lập bảng thống kê các chữ cái (không kể dấu) với tần số xuất hiện của chúng. Tìm các chữ cái xuất hiện từ ba lần trở kên và tính tần suất của các chữ cái đó.
168. Năng suất lúa của cả năm 1999 tính theo tạ/ha như sau (theo Niên giám 2000):

Lập biểu đồ cột đúng.

169. Cơ cấu kinh tế nước ta ( theo Niên giảm 2000):

Lập biểu đồ hình quạt cơ cấu kinh tế trong các năm trên.
170. Nhiệt độ không khí trung bình (tính theo độ C) trong các tháng năm 1999 của một số địa phương như sau (theo Niên giám 2000):

Trong mỗi địa phương trên:
a) Tháng nào nóng nhất? Tháng nào lạnh nhất?
b) Chênh lệch nhiệt độ giữa tháng nóng nhất và tháng lạnh nhất là bao nhiêu độ?

Tiết 12: Số trung bình cộng

Để địa diện cho một dấu hiệu, người ta thường dùng số trung bình cộng, đó là trung bình cộng của tất cả các giá trị được thống kê.
Có trường hợp người ta quan tâm đến giá trị có số lần xuất hiện nhiều nhất (tức là giá trị có tần số

lớn nhất), giá trị đó gọi là mốt (xem bài tập 175).

Ví dụ 48

Tính trung bình cộng điểm Toán của mỗi độ tuyển của trướng A và trường B trong ví dụ 47.

Giải:

Trung bình cộng điểm Toán của đội tuyển trường A:

(7+8.3+12.2+17+18.2+19):10=12,7.

Trung bình cộng điểm Toán của đội tuyển trường B:

(7+9.3+10.2+12.2+16+17+18):10=12,0.

Ví dụ 49

Trung bình cộng của tám số là 12. Do thêm số thứ chín nên trung bình cộng của chín số là 13. Tìm số thứ chín.

Giải:

Tổng của tám số lúc đầu là:12.8=96.

Tổng của chín số là: 13.9=117 .

Số thứ chín: 117 – 96=21 .

Bài tập

171. Điểm trung bình 10 bộ môn của hai học sinh An và Bách như sau:

An: 6,2; 6,3; 7,2; 7,5; 7,5;

       8,4; 8,6; 8,8; 8,8; 9,0.

Bách: 6,8; 6,8; 7,0; 7,0; 7,2;

          7,2; 7,2; 7,5; 7,5; 7,5.

Tính điểm trung bình các môn của mỗi học sinh trong các trường hợp sau:

a) Các môn không tính hệ số.

b) Một điểm 6,3 và một điểm 8,4 của An tính hệ số 2 , các điểm còn lại hệ số 1. Hai điểm 6,8 của Bách tính hệ số 2 , các điểm còn lại hệ số 1.
172. Điểm của Ban giám khảo cho các thí sinh A và B như sau:
Thí sinh A: 8; 8,5; 9; 9; 9.
Thí sinh B: 8; 8; 8,5; 8,5; 8.
Tính điểm trung bình của mỗi thí sinh.
173. Số giờ làm thêm của các công nhân hai tổ 1 và 2 trong một tháng như sau (mỗi tổ có 8 công nhân):
Tổ 1: 6, 6, 15, 18, 20, 20, 25, 30.
Tổ 2: 3, 6, 6, 10, 10, 15, 20, 30.
Tính số giờ làm thêm trung bình của các công nhân mỗi tổ.
174. Hai xạ thủ A và B thi bắn súng, mỗi người bắn 10 phát súng, kết quả điểm như sau:
A: 5, 7, 8, 10, 9, 7, 8, 10, 5, 8.
B: 7, 8, 6, 6, 7, 5, 6, 7, 6, 6.
Tính điểm trung bình của mỗi xạ thủ.
175. Các ngành kinh tế có dự án đầu tư trực tiếp của nước ngoài được cấp giấy phép trong năm 1999 như sau:

Ngành kinh tế nào có số dự án được cấp giấy phép nhiều nhất?
176. Trung bình cộng của các giá trị thay đổi thế nào nếu:
a) Mỗi giá trị tăng a đơn vị.
b) Mỗi giá trị tăng 10%
177. Một bảng thống kê cho biết tỉ số giữa số nữ và số nam là 11 : 10. Tuổi trung bình của nữ là 34, tuổi trung bình của nam là 32. Tính tuổi trung bình của những người được thống kê.
178. Trung bình cộng của sáu số là 4 . Do thêm số thứ bảy nên trung bình cộng của bảy số là 5 . Tìm số thứ bảy.
179. Một học sinh viết 27 rồi tính trung bình cộng của chúng, nhưng sau đó lại viết tiếp số trung bình cộng đó bên cạnh rồi tính luôn số trung bình cộng lúc đầu (trung bình cộng của 27 số).
180. Để tính trung bình cộng của ba số a, b, c bạn Tâm đã lấy trung bình cộng của a và b, rồi lấy trung
bình cộng của kết quả này và c. Cho biết a>b>c . Chứng minh rằng cách tính của Tâm cho kết quả nhỏ hơn kết quả đúng

Chương IV

Biểu thức đại số

Tiết 13: Giá trị của biểu thức đại số

Để tính giá trị của một biểu thức dại số tương ứng với một giá trị nào đó của biến số, ta thường thay giá trị đó của biến vào biểu thức rồi làm các phép tính theo thứ tự thực hiện đã được quy ước. Tuy nhiên trong một số bài, cần quan sát biểu thức để tính toán một cách hợp lí.
Ví dụ 50
Tính giá trị của biểu thức:

A= (1²+2²+3²+…+19²+20²)(a+b)(a+2b)(a+3b)

với \(a = \frac{3}{5}\), b= - 0,2

Giải: Chú ý rằng \(a + 3b = \frac{3}{5} + 3( - 0,2) = 0,6 - 0,6 = 0\)

Vậy A=0