Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Trắc nghiệm Toán lớp 7, tài liệu bao gồm 119 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt tài liệu

Chủ đề 1 -17 bài tập trắc nghiệm toán 7

Phần 1: Hướng dẫn làm bài tập trắc nghiệm

Do những thay đổi trong tính chất và phương pháp thi trong năm học này nên việc
ôn tập cũng phải thay đổi. Hình thức thi trắc nghiệm sẽ là phổ biến trong các môn thi. Để đáp ứng một bài thi trắc nghiệm cần phải đạt được 4 mức độ kiến thức:
1. Nhận biết
*Nhận biết có thể được hiểu là học sinh nêu hoặc nhận ra các khái niệm, nội dung, vấn đề
đã học khi được yêu cầu.
*Các hoạt động tương ứng với cấp độ nhận biết là: nhận dạng, đối chiếu, chỉ ra…
*Các động từ tương ứng với cấp độ nhận biết là: xác định, liệt kê, đối chiếu hoặc gọi tên,
giới thiệu, chỉ ra…nhận thức được những kiến thức đã nên trong sách giáo khoa.
Học sinh nhớ được (Bản chất) những khái niệm cơ bản của chủ đề và có thể nêu hoặc nhận
ra các khái niệm khi được yêu cầu. Đây là bậc thấp của nhận thức, khi học sinh kể tên, nêu
lại, nhớ lại một sự kiên, hiện tượng. Chẳng hạn ở mực độ này, học sinh chỉ cần có kiến
thức về hàm số bậc nhất để thay tọa độ điểm vào phương trình đường thẳng để tìm ra tọa
độ điểm phù hợp.
Ví dụ 1: Cho hai số nguyên x, y và \(y \ne 0\)Nếu x, y trái dấu thì số hữu tỉ \(a = \frac{x}{y}\)

A. a = 0

B. a > 0

C. a < 0

D. Cả B và C sai
Đáp án C

Ví dụ 2: Cặp số hữu tỉ nào dưới dây bằng nhau?
A. \(\frac{{ - 12}}{8}\) và \(\frac{3}{{ - 2}}\)

B. \(\frac{{10}}{{11}}\) và \(\frac{9}{{10}}\)

C. \(\frac{6}{8}\) và \(\frac{{12}}{{15}}\)

D. \(\frac{5}{7}\) và \(\frac{7}{5}\)

Đáp án A
Ví dụ 3: Biểu đồ dân số Việt Nam qua tổng điều tra trong thế
kỉ XX (đơn vị của các cột là triệu người)
Chon câu trả lời sai

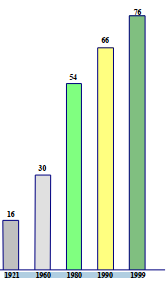
A. Năm 1921 số dân của nước ta là 16 triệu người
B. Năm 1960 số dân của nước ta là 30 nghìn người
C. Năm 1980 số dân của nước ta là 66 triệu người
D. Năm 1999 số dân của nước ta là 76 triệu người
Đáp án C
2. Thông hiểu
*Học sinh hiểu các khái niệm cơ bản, có khả năng diễn đạt được kiến thức đã học
theo ý hiểu của mình và có thể sử dụng khi câu hỏi được đặt ra tương tự hoặc gần với các
ví dụ học sinh đã được học trên lớp.
*Các hoạt động tương ứng với cấp độ thông hiểu là: diễn giải, kể lại, viết lại, lấy
được ví dụ theo các hiểu của mình.
*Các động từ tương ứng với cấp độ thông hiểu có thể là: Tóm tắt, giải thích, mô tả,
so sánh (đơn giản), phân biệt, trình bày lại, viết lại, minh họa, hình dung, chứng tỏ,
chuyển đổi…
Học sinh hiểu các khái niệm cơ bản và có thể sử dụng khi câu hỏi được đặt ra gần
với các ví dụ học sinh đã được học trên lớp.
Ví dụ 1. Cho đoạn thẳng AB dài 8cm. Lấy điểm M trên đoạn thẳng AB sao cho AM = 6
cm. Đường thẳng d là đường trung trực của MB, d cắt MB tại K. Khẳng định nào dưới đây
sai?
A. KB cm =1 .

B. KA cm = 7 .

C.\(d \bot AB\).

D. d // AB .
Ví dụ 2. Có bao nhiêu số \(x \in Q\)thỏa mãn |2x+3|+|5 – 3x|?
A. Không có.

B. Có một số.

C. Có hai số.

D. Có ba số.
Ví dụ 3. Theo dõi các bạn nghỉ học ở từng buổi trong một tháng, bạn lớp trưởng ghi lại như sau:

0	0	0	1	0	3	2	0	3	0	1	0	1
1	0	0	1	0	0	1	2	2	2	0	1	0

Dấu hiệu ở đây là gì?
A. Tổng số lượt học sinh nghỉ học cả tháng.
B. Là các số 0, 1, 2, 3.
C. Số học sinh nghỉ học trong mỗi buổi.
D. Mỗi tháng học có 26 buổi.
Đáp án C
3. Vận dụng
*Học sinh vượt qua cấp độ hiểu đơn thuần và có thể sử dụng, xử lý các khái niệm
của chủ đề trong các tình huống tương tự nhưng không hoàn toàn giống nhau như tình huống đã gặp trên lớp. Học sinh có khả năng sử dụng kiến thức, kĩ năng đã học trong những tình huống cụ thể, tình huống tương tự nhưng không hoàn toàn giống như tình huống đã học trên lớp (thực hiện nhiệm vụ quen thuộc nhưng mới hơn thông thường) .
*Các hoạt động tương ứng với vận dụng ở cấp độ thấp là: xây dựng mô hình,
phỏng vấn, trình bày, tiến hành thí nghiệm, xây dựng các phân loại, áp dụng quy tắc (định lý, định luật, mệnh đề…), sắm vai và đảo vai trò….

*Các động từ tương ứng với vận dụng ở cấp độ thấp có thể là: thực hiện, giải quyết, minh họa, tính toán, diễn dịch, bày tỏ, áp dụng, phân loại, sửa đổi, đưa vào thực tế, chứng minh, ước tính, vận hành, …
Học sinh vượt qua cấp độ hiểu đơn thuần và có thể áp dụng các khái niệm của chủ
đề trong các tình huống tương tự trên lớp để giải quyết một tình huống cụ thể trong thực tế hoặc học sinh cá khả năng sử dụng các khái niệm cơ bản để giải quyết một vấn đề mới chưa từng được học hoặc trải nghiệm trước đấy, nhưng có thể giải quyết bằng kỹ năng, kiến thức và thái độ đã được học tập và rèn luyện. Các vấn đề này tương tự như các tình huống thực tế học sinh sẽ gặp ngoài môi trương

Ví dụ 1. Tìm \(x \in Q\)thỏa mãn |x – 2| +|x+1|=2x

A. \(x = \frac{3}{2}\)

B. \(x =  - \frac{3}{2}\)

C. \(x = \frac{{ - 1}}{2}\)

D. x = 0

Đáp án A

Ví dụ 2. Giá trị của biểu thức Q = x³y⁵ – 2xy tại \(x = \frac{1}{3}\) và y = - 1 bằng

A. \(\frac{{17}}{{27}}\)

B. \(\frac{{ - 17}}{{27}}\)

C. \(\frac{{19}}{{27}}\)

D. 1

Đáp án A

Ví dụ 3. Cho a // b và \(\widehat {{A_1}} + \widehat {{B_1}} = {100^0}\) ( hình vẽ bên).

Số đo góc \(\widehat {{A_1}}\) bằng:

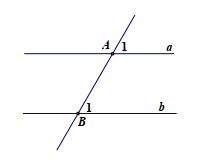
A. 10⁰

B. 90⁰

C. 45⁰

D. 50⁰

Đáp án D

4. Vận dụng ở mức độ cao hơn
Học sinh có khả năng sử dụng các khái niệm cơ bản để giải quyết một vấn đề mới
hoặc không quen thuộc, chưa từng được học hoặc trải nghiệm trước đây, nhưng có thể giải quyết bằng các kỹ năng và kiến thức đã được dạy ở mức độ tương đương. Những vấn đề này tương tự như các tình huống thực tế học sinh sẽ gặp ngoài môi trường lớp học.
Ở mức độ này học sinh phải xác định được những thành tố trong 1 tổng thể và mối
quan hệ qua lạị giữa chúng, phát biểu ý kiến cá nhân và bảo vệ được ý kiến đó về 1 sự kiện, hiện tượng hay nhân vật lịch sử nào đó.

Ví dụ 1. Cho a//b như hình vẽ bên. Số đo góc x bằng:

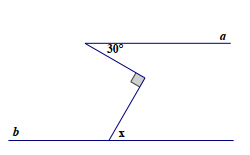
A. 150⁰

B. 90⁰

C. 60⁰

D. 30⁰.

Đáp án C

Ví dụ 2. Cho hai đa thức P(x) = x⁴ + 2x³ + x² + 5x và Q(x) = x⁴ + x³ – x² +6x +2, gọi H(x) = P(x) – Q(x). Hỏi đa thức H(x) có bao nhiêu nghiệm?

A. 1.

B. 2.

C. 3.

D. 4.

Đáp án C

Ví dụ 3. Cho \(H =  & \frac{9}{{\sqrt x  + 2}}\)Hỏi có bao nghiệm x để H có giá trị nguyên?

A. 2 .

B. 3.

C. 5.

D. 6.

Đáp án A

Ở bài thi trắc nghiệm thường sẽ là những bài yêu cầu giải nhanh và không qua
rườm rà, yêu cầu kiến thức rộng và bao quát hơn. Nếu như các em đang theo phương pháp “chậm và chắc” thì bạn phải đổi ngay từ “chậm” thành “nhanh”. Giải nhanh chính là chìa khóa để bạn có được điểm cao ở môn thi trắc nghiệm. Với các bài thi nặng về lý thuyết thì sẽ yêu cầu ghi nhớ nhiều hơn, các em nên chú trọng phần liên hệ.
Ngoài việc sử dụng kiến thức để làm bài thi, các em có thể vận dụng thêm các phương pháp sau đây:
- Phương pháp phỏng đoán: Dựa vào kiến thức đã học, đưa ra phỏng đoán để tiết
kiệm thời gian làm bài.
- Phương pháp loại trừ:
Một khi các em không có cho mình mottj đáp án thực sự chính xác thì phương pháp loại trừ cũng là một các hữu hiệu giúp bạn tìm ra câu trả lời đúng. Mỗi câu hỏi thường có 4 đáp án, các đáp án cũng thường không khác nhau nhiều lắm về nội dung, tuy nhiên vẫn có cơ sở để các em dùng phương án loại trừ bằng “mẹo” của mình cộng thêm chút may mắn nữa. Tháy vì đi tìm đáp án đứng, bạn hãy thử tìm phương án sai… đó cũng là một cách hay và loại trừ càn nhiều phương án càng tốt.
Khi các em không còn đủ cơ sở để loại trừ nữa thì hãy dùng cách phỏng đoán, nhận thấy phương án nào khả thi thi hơn và đủ tin cậy hơn thì khoanh vào phiếu trả lời. Đó là cách cuối cùng dành cho các em.
Thi trắc nghiệm nhằm mục đích vừa đảm bảo hiểu rộng kiến thức vừa đảm bảo
thời gian nên các em cần phải phân bố thời gian cho hợp lý nhất.

Chủ đề 1

Bốn phép toán trên tập số hữu tỉ

1. Một số vấn đề cần ôn tập

Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với \(a,b \in \mathbb{Z};b \ne 0\)

Tập hợp các số hữu tỉ được kí hiệu là Q.

Cộng và trừ số hữu tỉ:

Cho hai số hữu tỉ x, y : \(x = \frac{a}{m};y = \frac{b}{m}(a,b,m \in \mathbb{Z},m \ne 0)\)

\(a + b = \frac{a}{m} + \frac{b}{m} = \frac{{a + b}}{m};x - y = \frac{a}{m} - \frac{b}{m} = \frac{{a - b}}{m}\)

Nhân và chia hai số hữu tỉ:

Cho hai số hữu tỉ u, v: \(u = \frac{a}{b};v = \frac{c}{d}(a,b,c,d \in \mathbb{Z};b,d \ne 0)\)

\(u.v = \frac{a}{b}.\frac{c}{d} = \frac{{ac}}{{bd}}\)

Nếu \(v \ne 0\) thì \(u:v = \frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{ad}}{{bc}}\)

Số hữu tỉ \(x \ne 0\) có số nghịch đảo là \(\frac{1}{x}\)

Tính chất: Cho các số hữu tỉ x, y, z. Ta có:

Tính chất giao hoán: x+y =y+x ; x.y=y.x

Tính chất kết hợp: (x+y)+z=x +(y +z); (x.y).z=x.(y.z)

Tính chất cộng với 0: x+0 = 0+x=x

Tính chất nhân với số 1:x.1=1.x=x

Tính chất nhân với 0: x.0 = 0.x =0

Tính chất phân phối của phép nhân với phép cộng:

x.(y+z) = x.y+x.z

Một số phép toán hay sử dụng: \(\frac{{x + y}}{z} = \frac{x}{z} + \frac{y}{z};\frac{{x - y}}{z} = \frac{x}{z} - \frac{y}{z}\), với \(z \ne 0\)

\(x.y = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\y = 0\end{array} \right.\)

-(x.y)= - x.y =x.( - y)

Chú ý không có tính chất: x:y +x:z = x:(y+z)

Xem thêm