Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các dạng toán trắc nghiệm góc lượng giác và công thức lượng giác, tài liệu bao gồm 54 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Góc và cung lượng giác

Phần A. Câu hỏi.

Dạng 1. Mối liên hệ giũ̉a radian và độ

Dạng 2. Đường tròn lượng giác và các bài toán liên quan.

Phần B. Lời giải

Dạng 1. Mối liên hệ giũa radian và độ

Dạng 2. Đường tròn lượng giác và các bài toán liên quan.

Các dạng toán trắc nghiệm góc lượng giác và công thức lượng giác

Phần A. Câu hỏi

Dạng 1. Mối liên hề giữa radian và độ

Câu 1. Số đo theo đơn vị rađian của góc ${315}^{°}$ là

A. \(\frac{{7\pi }}{2}\).

B. \(\frac{{7\pi }}{4}\).

C. \(\frac{{2\pi }}{7}\).

D. \(\frac{{4\pi }}{7}\).

Câu 2. Cung tròn có số đo là \(\frac{{5\pi }}{4}\). Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.

A. $5^{°}$.

B. ${15}^{°}$.

C. ${172}^{°}$.

D. ${255}^{°}$.

Câu 3. Cung tròn có số đo là \(\pi \). Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.

A. ${30}^{°}$.

B. ${45}^{°}$.

C. ${90}^{°}$.

D. ${180}^{°}$.

Câu 4. Góc ${63}^{°}{48}^{\text{'}}$ bằng (với \(\pi  = 3,1416\) )

A. \(1,113{\rm{rad}}\).

B. \(1,108{\rm{rad}}\).

C. \(1,107{\rm{rad}}\).

D. \(1,114{\rm{rad}}\).

Câu 5. Góc có số đo \(\frac{{2\pi }}{5}\) đổi sang độ là:

A. ${135}^{°}$.

B. \({72^0}\).

C. ${270}^{°}$.

D. ${240}^{°}$.

Câu 6. Góc có số đo \({108^0}\) đổi ra rađian là:

A. \(\frac{{3\pi }}{5}\).

B. \(\frac{\pi }{{10}}\).

C. \(\frac{{3\pi }}{2}\).

D. \(\frac{\pi }{4}\).

Câu 7. Góc có số đo \(\frac{\pi }{9}\) đổi sang độ là:

A. ${25}^{°}$.

B. ${15}^{°}$.

C.${18}^{°}$.

D. ${20}^{°}$.

Câu 8. Cho \(a = \frac{\pi }{2} + k2\pi \). Tìm k để \(10\pi  < a < 11\pi \)

A. \(k = 7\).

B. \(k = 5\).

C. \(k = 4\).

D. \(k = 6\).

Câu 9. Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là:

A. ${60}^{°}$.

B. ${30}^{°}$.

C. ${40}^{°}$.

D. ${50}^{°}$.

Câu 10. Đổi số đo góc ${105}^{°}$ sang rađian.

A. \(\frac{{7\pi }}{{12}}\).

B. \(\frac{{9\pi }}{{12}}\).

C. \(\frac{{5\pi }}{8}\).

D. \(\frac{{5\pi }}{{12}}\).

Câu 11. Số đo góc \({22^0}{30^\prime }\) đổi sang rađian là:

A. \(\frac{\pi }{5}\).

B. \(\frac{\pi }{8}\).

C. \(\frac{{7\pi }}{{12}}\).

D. \(\frac{\pi }{6}\).

Câu 12. Một cung tròn có số đo là ${45}^{°}$. Hãy chọn số đo radian của cung tròn đó trong các cung tròn sau đây.

A. \(\frac{\pi }{2}\)

B. \(\pi \)

C. \(\frac{\pi }{4}\)

D. \(\frac{\pi }{3}\)

Câu 13. Góc có số đo \(\frac{\pi }{{24}}\) đổi sang độ là:

A. \({7^0}\).

B. \({7^0}{30^\prime }\).

C. \({8^0}\).

D. \({8^0}{30^\prime }\).

Câu 14. Góc có số đo ${120}^{°}$đổi sang rađian là:

A. \(\frac{{2\pi }}{3}\).

B. \(\frac{{3\pi }}{2}\).

C. \(\frac{\pi }{4}\).

D. \(\frac{\pi }{{10}}\).

Dạng 2. Đường tròn lượng giác và các bài toán liên quan

Câu 15. Một đồng hồ treo tường, kim giờ dài 10,57cm và kim phút dài 13,34cm.Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là

A. 2,78cm .

B. 2,77cm .

C. 2,76cm .

D. 2,8cm .

Câu 16. Cung tròn bán kính bằng 8,43cm có số đo 3,85rad có độ dài là

A.  32,46cm

B. 32,47cm .

C. 32,5cm .

D. 32,45cm .

Câu 17. Trên đường tròn với điểm gốc là A. Điểm M thuộc đường tròn sao cho cung lượng giác AM có số đo ${60}^{°}$. Gọi N là điểm đối xứng với điểm M qua trục Oy, số đo cung AN là

A. $-{120}^{°}$ hoặc ${240}^{°}$.

B. ${120}^{°}+k{360}^{°},k\in \mathbb{Z}$.

C. ${120}^{°}$.

D. $-{240}^{°}$.

Câu 18. Trong 20 giây bánh xe của xe gắn máy quay được 60 vòng.Tính độ dài quãng đường xe gắn máy đã đi được trong vòng 3 phút,biết rằng bán kính bánh xe gắn máy bằng 6,5cm (lấy \(\pi  = 3,1416\) )

A.  22043 cm

B.  22055 cm

C.  22042 cm

D. 22054 cm

Câu 19. Trên đường tròn bán kính r=15, độ dài của cung có số đo ${50}^{°}$ là:

A. \(l = 15.\frac{{180}}{\pi }\).

B. \(l = \frac{{15\pi }}{{180}}\).

C. \(l = 15.\frac{{180}}{\pi }.50\).

D. \(l = 750\).

Câu 20. Cho bốn cung (trên một đường tròn định hướng): \(\alpha  =  - \frac{{5\pi }}{6},\beta  = \frac{\pi }{3},\gamma  = \frac{{25\pi }}{3},\delta  = \frac{{19\pi }}{6}\), Các cung nào có điểm cuối trùng nhau:

A. \(\beta \) và \(\gamma ;\alpha \) và \(\delta \).

B. \(\alpha ,\beta ,\gamma \).

C. \(\beta ,\gamma ,\delta \).

D. \(\alpha \) và \(\beta ;\gamma \) và \(\delta \).

Câu 21. Cho L, M, N, P lần lượt là điểm chính giữa các cung AB, BC, CD, DA. Cung \(\alpha \) có mút đầu trùng với A và số đo \(\alpha  =  - \frac{{3\pi }}{4} + k\pi \). Mút cuối của \(\alpha \) ở đâu?

A. L hoặc N.

B. M hoặc P.

C. M hoặc N.

D. L hoặc P.

Câu 22. Trên đường tròn bán kính r= 5, độ dài của cung đo \(\frac{\pi }{8}\) là:

A. \(l = \frac{\pi }{8}\).

B. \(l = \frac{{r\pi }}{8}\).

C. \(l = \frac{{5\pi }}{8}\).

D. kết quả khác.

Câu 23. Một đường tròn có bán kính R=10cm. Độ dài cung ${40}^{°}$ trên đường tròn gần bằng

A. 11cm.

B. 13cm.

C. 7cm.

D. 9cm.

Câu 24. Biết một số đo của góc \(\angle (Ox,Oy) = \frac{{3\pi }}{2} + 2001\pi \). Giá trị tổng quát của góc \(\angle (Ox,Oy)\) là:

A. \(\angle (Ox,Oy) = \frac{{3\pi }}{2} + k\pi \).

B. \(\angle (Ox,Oy) = \pi  + k2\pi \).

C. \(\angle (Ox,Oy) = \frac{\pi }{2} + k\pi \).

D. \(\angle (Ox,Oy) = \frac{\pi }{2} + k2\pi \).

Câu 25. Cung nào sau đây có mút trung với B hoặc \({\rm{B}}\) '?

A. $a={90}^{°}+k{360}^{°}$.

B. $a=-{90}^{°}+k{360}^{°}$.

C. \(\alpha  = \frac{\pi }{2} + k2\pi \).

D. \(\alpha  =  - \frac{\pi }{2} + k2\pi \).

Câu 26. Cung \(\alpha \) có mút đầu là A và mút cuối là M thì số đo của \(\alpha \) là:

A. \(\frac{{3\pi }}{4} + k2\pi \).

B. \( - \frac{{3\pi }}{4} + k2\pi \).

C. \(\frac{{3\pi }}{4} + k\pi \).

D. \( - \frac{{3\pi }}{4} + k\pi \).

Câu 27. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Trên hình vẽ hai điểm M,N biểu diễn các cung có số đo là:

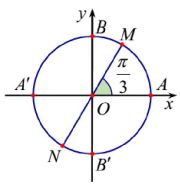
A. \(x = \frac{\pi }{3} + 2k\pi \).

B. \(x =  - \frac{\pi }{3} + k\pi \).

C. \(x = \frac{\pi }{3} + k\pi \).

D. \(x = \frac{\pi }{3} + k\frac{\pi }{2}\).

Câu 28. Trên đường tròn lượng giác gốc A, cho điểm M xác định bởi sđ \(AM = \frac{\pi }{3}\). Gọi \({M_1}\) là điểm đối xứng của M qua trục Ox. Tìm số đo của cung lượng giác \(A{M_1}\).

A. sđ \(A{M_1} = \frac{{ - 5\pi }}{3} + k2\pi ,k \in \mathbb{Z}\)

B. sđ \(A{M_1} = \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\)

C. sđ \(A{M_1} = \frac{{ - \pi }}{3} + k2\pi ,k \in \mathbb{Z}\)

D. sđ \(A{M_1} = \frac{{ - \pi }}{3} + k\pi ,k \in \mathbb{Z}\)

Câu 29. Góc lượng giác nào sau đây có cùng điểm cuối với góc \(\frac{{7\pi }}{4}\) ?

A. \( - \frac{\pi }{4}\).

B. \(\frac{\pi }{4}\).

C. \(\frac{{3\pi }}{4}\).

D. \( - \frac{{3\pi }}{4}\).

Câu 30. Có bao nhiêu điểm M trên đương tròn định hương gốc A thỏa mãn .

A. 6 .

B. 4 .

C. 3 .

D. 8 .

Phần B. Lời giải

Dạng 1. Mối liên hệ giữa radian và độ

Câu 1. Chọn B

Ta có ${315}^{°}=\frac{315}{180}.\pi =\frac{7\pi }{4}($radian).

Câu 2. Chọn D

Ta có: $a^{°}=\frac{\alpha }{\pi }\cdot {180}^{°}=\frac{\frac{5\pi }{4}}{\pi }\cdot {180}^{°}={225}^{°}$

Câu 3. Chọn D

Ta có:$a^{°}=\frac{\alpha }{\pi }\cdot {180}^{°}={180}^{°}$.

Câu 4. Chọn D

Ta có:\({\rm{ }}{63^0}{48^\prime } = 63,{8^0} = \frac{{63,{8^0} \times 3,1416}}{{{{180}^0}}} \approx 1,114{\rm{rad}}\)

Câu 5. Chọn B

Ta có \(\frac{{2\pi }}{5} = \frac{{{{2.180}^0}}}{5} = {72^0}\)

Câu 6. Chọn A

Ta có :\({108^0} = \frac{{{{108}^0}.\pi }}{{{{180}^0}}} = \frac{{3\pi }}{5}\)

Câu 7. Chọn D

Ta có :$\frac{\pi }{9}=\frac{{180}^{°}}{9}={20}^{°}$

Câu 8. Chọn B

Để \(10\pi  < a < 11\pi {\rm{ th\`i  }}\frac{{19\pi }}{2} < k2\pi  < \frac{{21\pi }}{2} \Rightarrow k = 5\)

Câu 9. Chọn D

1 bánh răng tương ứng với $\frac{{360}^{°}}{72}=5^0\Rightarrow 10\text{ banh rang là }{50}^{°}.$

Câu 10. Chọn A

${105}^0=\frac{{105}^{°}\cdot \pi }{{180}^0}=\frac{7\pi }{12}$

Câu 11. Chọn B

\({22^0}{30^\prime } = \frac{{{{22}^0}{{30}^\prime }.\pi }}{{{{180}^0}}} = \frac{\pi }{8}\)

Câu 12. Chọn \(C\)

Ta có: $\alpha =\frac{a^{°}\cdot \pi }{{180}^{°}}=\frac{\pi }{4}\text{. }$

Câu 13. Chọn B

Ta có:$\frac{\pi }{24}=\frac{{180}^{°}}{24}=7^0{30}^{\text{'}}\text{. }$

Câu 14. Chọn A

Ta có:${120}^{°}=\frac{{120}^{°}.\pi }{{180}^0}=\frac{2\pi }{3}\text{. }$

Dạng 2. Đường tròn lượng giác và các bài toán liên quan

Câu 15. Chọn B

6 giờ thì kim giờ vạch lên 1 cung có số đo \(\pi \) nên 30 phút kim giờ vạch lên 1 cung có số đo là \(\frac{1}{{12}}\pi \), suy ra độ dài cung tròn mà nó vạch lên là \(l = R\alpha  = 10,57 \times \frac{{3,14}}{{12}} \approx 2,77\)

Câu 16. Chọn A

Độ dài cung tròn là \(l = R\alpha  = 8,43 \times 3,85 = 32,4555\)

Câu 17. Chọn C

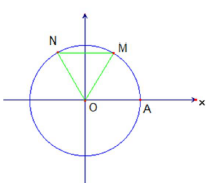
Ta có: $\widehat{AON}={60}^{°},\widehat{MON}={60}^{°}$ nên $\widehat{AOM}={120}^{°}$. Khi đó số đo cung AN bằng ${120}^{°}$.

Câu 18. Chọn D

3 phút xe đi được \(\frac{{3 \times 60}}{{20}} \times 60 = 540\) vòng. Độ dài 1 vòng bằng chu vi bánh xe là \(2\pi R = 2 \times 3,1416 \times 6,5 = 40,8408\). Vậy quãng đường xe đi được là\(540 \times 40,8408 = 22054,032\;{\rm{cm}}\)

Câu 19. Chọn \({\bf{C}}\)

\(l = \frac{{\pi  \cdot r \cdot {{\rm{n}}^0}}}{{{{180}^0}}} = \frac{{\pi 15.50}}{{180}}\)

Câu 20. Chọn A

C1: Ta có: \(\delta  - \alpha  = 4\pi  \Rightarrow 2\) cung \(\alpha \) và \(\delta \) có điểm cuối trùng nhau.

\(\gamma  - \beta  = 8\pi  \Rightarrow \) hai cung \(\beta \) và \(\gamma \) có điểm cuối trùng nhau.

C2: Gọi là điểm cuối của các cung \(\alpha ,\beta ,\gamma ,\delta \)

Biểu diễn các cung trên đường tròn lượng giác ta có \(B \equiv C,A \equiv D\).

Câu 21. Chọn A

Nhìn vào đường tròn lượng giác để đánh giá.                                               

Câu 22. Chọn C

Độ dài cung \({\rm{AB}}\) có số đo cung \({\rm{AB}}\) bằng n độ: \(l = r \cdot n = 5 \cdot \frac{\pi }{8}\).