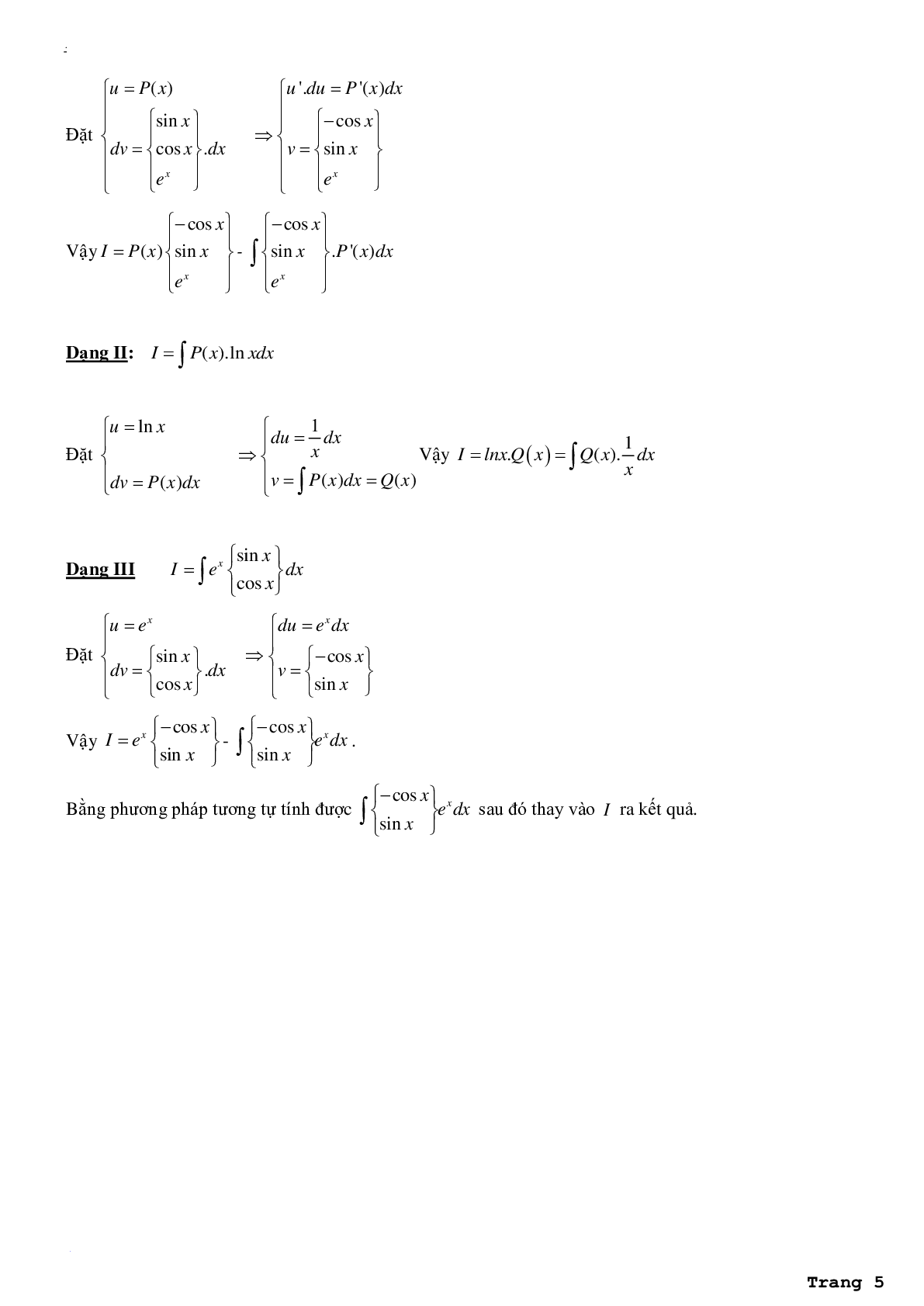Chuyên đề tự luận nguyên hàm tích phân và ứng dụng

Chuyên đề tự luận nguyên hàm tích phân và ứng dụng - Nguyễn Chiến

Quang Trung Ngày: 08-03-2024 Lớp 12

Tải xuống 67 759 8

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề tự luận nguyên hàm tích phân và ứng dụng - Nguyễn Chiến, tài liệu bao gồm 67 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề tự luận nguyên hàm tích phân và ứng dụng - Nguyễn Chiến

Nguyên hàm - tích phân - ứng dụng tích phân

I. Nguyên hàm

1. Nguyên hàm

Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu ${F^\prime }(x) = f(x)$ với mọi $x \in K$

Kí hiệu: $\int f (x)d{\rm{x}} = F(x) + C$.

Định lí:

1) Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó $F(x) + C,C \in \mathbb{R}$ là họ tất cả các nguyên hàm của f(x) trên K.

2. Tính chất của nguyên hàm

- ${\left( {\int f (x)d{\rm{x}}} \right)^\prime } = f(x)$ và $\int {{f^\prime }} (x)d{\rm{x}} = f(x) + C;d\left( {\int f (x){\rm{dx}}} \right) = f(x){\rm{dx}}$

- Nếu F(x) có đạo hàm thì: $\int d (F(x)) = F(x) + C$

- $\int k f(x)d{\rm{x}} = k\int f (x)d{\rm{x}}$ với k là hằng số khác 0 .

- \[\smallint [f(x) \pm g(x)]d{\rm{x}} = \smallint f(x)d{\rm{x}} \pm \smallint g(x)d{\rm{x}}\]

- Công thức đổi biến số: Cho y = f(x) và u = g(x).

Nếu $\int f (x)dx = F(x) + C$ thì $\int f (g(x)){g^\prime }(x)dx = \int f (u)du = F(u) + C$

3. Sự tồn tại của nguyên hàm

Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

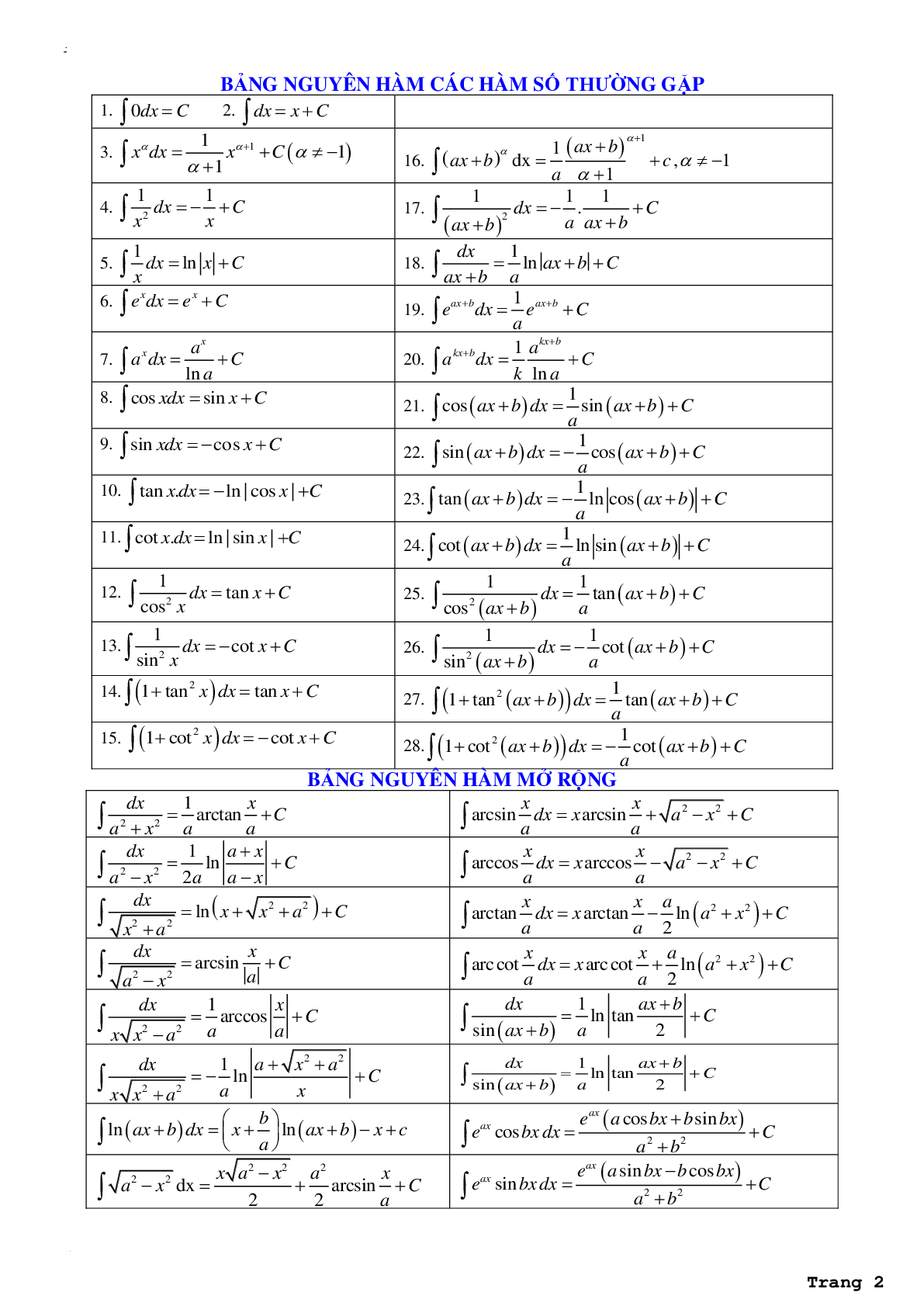
BẢNG NGUYÊN HÀM CÁC HÀM SỐ THƯỜNG GẶP

1. $\int 0 dx = C\quad $	16. $\int {{{(ax + b)}^\alpha }} {\rm{dx}} = \frac{1}{a}\frac{{{{(ax + b)}^{\alpha + 1}}}}{{\alpha + 1}} + c,\alpha \ne - 1$
2. $\int d x = x + C$	17. $\int {\frac{1}{{{{(ax + b)}^2}}}} dx = - \frac{1}{a} \cdot \frac{1}{{ax + b}} + C$
3. $\int {{x^\alpha }} dx = \frac{1}{{\alpha + 1}}{x^{\alpha + 1}} + C(\alpha \ne - 1)$	18. $\int {\frac{{dx}}{{ax + b}}} = \frac{1}{a}\ln \|ax + b\| + C$
4. $\int {\frac{1}{{{x^2}}}} dx = - \frac{1}{x} + C$	19. $\int {{e^{ax + b}}} dx = \frac{1}{a}{e^{ax + b}} + C$ 20. $\int {{a^{k + h}}} dx = \frac{1}{k}\frac{{{a^{k + \delta }}}}{{\ln a}} + C$
5. $\int {\frac{1}{x}} dx = \ln \|x\| + C$	21. $\int {\cos } (ax + b)dx = \frac{1}{a}\sin (ax + b) + C$
6. $\int {{e^x}} dx = {e^x} + C$	22. $\int {\sin } (ax + b)dx = - \frac{1}{a}\cos (ax + b) + C$
7. $\int {{a^x}} dx = \frac{{{a^x}}}{{\ln a}} + C$	23. $\int {\tan } (ax + b)dx = - \frac{1}{a}\ln \|\cos (ax + b)\| + C$
8. $\int {\cos } xdx = \sin x + C$	24. $\int {\cot } (ax + b)dx = \frac{1}{a}\ln \|\sin (ax + b)\| + C$
9. $\int {\sin } xdx = - \cos x + C$	25. $\int {\frac{1}{{{{\cos }^2}(ax + b)}}} dx = \frac{1}{a}\tan (ax + b) + C$
10. $\int {\tan } x \cdot dx = - \ln \|\cos x\| + C$	26. $\int {\frac{1}{{{{\sin }^2}(ax + b)}}} dx = - \frac{1}{a}\cot (ax + b) + C$
11. $\int {\cot } xdx = \ln \|\sin x\| + C$	27. $\int {\left( {1 + {{\tan }^2}(ax + b)} \right)} dx = \frac{1}{a}\tan (ax + b) + C$
12. $\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C$	28. $\int {\left( {1 + {{\cot }^2}(ax + b)} \right)} dx = - \frac{1}{a}\cot (ax + b) + C$
13. $\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C$
14. $\int {\left( {1 + {{\tan }^2}x} \right)} dx = \tan x + C$
15. $\int {\left( {1 + {{\cot }^2}x} \right)} dx = - \cot x + C$

BẢNG NGUYÊN HÀM MỞ RỘNG

$\int {\frac{{dx}}{{{a^2} + {x^2}}}} = \frac{1}{a}\arctan \frac{x}{a} + C$	$\int {\arcsin } \frac{x}{a}dx = x\arcsin \frac{x}{a} + \sqrt {{a^2} - {x^2}} + C$
$\int {\frac{{dx}}{{{a^2} - {x^2}}}} = \frac{1}{{2a}}\ln \left\| {\frac{{a + x}}{{a - x}}} \right\| + C$	$\int {\arccos } \frac{x}{a}dx = x\arccos \frac{x}{a} - \sqrt {{a^2} - {x^2}} + C$
$\int {\frac{{dx}}{{\sqrt {{x^2} + {a^2}} }}} = \ln \left( {x + \sqrt {{x^2} + {a^2}} } \right) + C$	$\int {\arctan } \frac{x}{a}dx = x\arctan \frac{x}{a} - \frac{a}{2}\ln \left( {{a^2} + {x^2}} \right) + C$
$\int {\frac{{dx}}{{\sqrt {{a^2} - {x^2}} }}} = \arcsin \frac{x}{{\|a\|}} + C$	$\int {{\mathop{\rm arccot}\nolimits} } \frac{x}{a}dx = x{\mathop{\rm arccot}\nolimits} \frac{x}{a} + \frac{a}{2}\ln \left( {{a^2} + {x^2}} \right) + C$
$\int {\frac{{dx}}{{x\sqrt {{x^2} - {a^2}} }}} = \frac{1}{a}\arccos \left\| {\frac{x}{a}} \right\| + C$	$\int {\frac{{dx}}{{\sin (ax + b)}}} = \frac{1}{a}\ln \left\| {\tan \frac{{ax + b}}{2}} \right\| + C$
$\int {\frac{{dx}}{{x\sqrt {{x^2} + {a^2}} }}} = - \frac{1}{a}\ln \left\| {\frac{{a + \sqrt {{x^2} + {a^2}} }}{x}} \right\| + C$	$\int {\frac{{dx}}{{\sin (ax + b)}}} = \frac{1}{a}\ln \left\| {\tan \frac{{ax + b}}{2}} \right\| + C$
$\int {\ln } (ax + b)dx = \left( {x + \frac{b}{a}} \right)\ln (ax + b) - x + c$	$\int {{e^{ax}}} \cos bxdx = \frac{{{e^{ax}}(a\cos bx + b\sin bx)}}{{{a^2} + {b^2}}}$
$\int {\sqrt {{a^2} - {x^2}} } dx = \frac{{x\sqrt {{a^2} - {x^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{x}{a} + C$	$\int {\sin } bxdx = \frac{{{e^{ax}}(a\sin bx - b\cos bx)}}{{{a^2} + {b^2}}} + C$

Các phương pháp tính nguyên hàm

1. Phương pháp đổi biến

a. Đổi biến dạng 1:

Nếu $\int f (x) = F(x) + C$ và với $u = \varphi (t)$ là hàm số có đạo hàm thì : $\int f (u)du = F(u) + C$

Phương pháp chung

- Bước 1: Chọn $x = \varphi (t)$, trong đó $\varphi (t)$ là hàm số mà ta chọn thích hợp .

- Bước 2: Lấy vi phân hai vế : $dx = {\varphi ^\prime }(t)dt$

- Bước 3: Biến đổi : $f(x)dx = f[\varphi (t)]{\varphi ^\prime }(t)dt = g(t)dt$

- Bước 4: Khi đó tính : $\int f (x)dx = \int g (t)dt = G(t) + C$.

* Các dấu hiệu đổi biến thường gặp :

Dấu hiệu	Cách chọn
$\sqrt {{a^2} - {x^2}} $	Đặt $x = \|a\|\sin t;$ với $t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \cdot $ hoặc $x = \|a\|\cos t;$ với $t \in [0;\pi ].$
$\sqrt {{x^2} - {a^2}} $	Đặt $x = \frac{{\|{\rm{a}}\|}}{{\sin t}} \cdot ;$ với $t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\backslash \{ 0\} $ hoặc $x = \frac{{\|a\|}}{{\cos t}}$ với$t \in [0;\pi ]\backslash \left\{ {\frac{\pi }{2}} \right\}.$
$\sqrt {{a^2} + {x^2}} $	Đặt $x = a\tan t;$ với $t \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right).$ hoặc x = \|a\|cott với $t \in [0;\pi ].$
$\sqrt {\frac{{a + x}}{{a - x}}} .$ hoặc $\sqrt {\frac{{a - x}}{{a + x}}} .$	Đặt $x = a\cos 2t$
$\sqrt {(x - a)(b - x)} $	Đặt $x = a + (b - a){\sin ^2}t$
$\frac{1}{{{a^2} + {x^2}}}$	Đặt $x = a\tan t;$ với $t \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right).$

b. Đổi biến dạng 2:

Nếu hàm số f(x) liên tục thì đặt $x = \varphi (t)$. Trong đó $\varphi (t)$ cùng với đạo hàm của nó $\left( {{\varphi ^\prime }(t)} \right.$ là những hàm số liên tục) thì ta được :

$\int f (x)dx = \int f [\varphi (t)]{\varphi ^\prime }(t)dt = \int g (t)dt = G(t) + C.$

Phương pháp chung.

- Bước 1: Chọn $t = \varphi (x)$. Với $\varphi (x)$ là hàm số mà ta chọn thích hợp.

- Bước 2: Tính vi phân hai vế : $dt = {\varphi ^\prime }(t)dt$.

- Bước 3: Biểu thị : $f(x)dx = f[\varphi (t)]{\varphi ^\prime }(t)dt = g(t)dt$.

- Bước 4: Khi đó : $I = \int f (x)dx = \int g (t)dt = G(t) + C$

* Các dấu hiệu đổi biến thường gặp :

Dấu hiệu	Cách chọn
Hàm số mẫu số có	t là mẫu số
Hàm $f(x;\sqrt {\varphi (x)} )$	$t = \sqrt {\varphi (x)} $
Hàm $f(x) = \frac{{a \cdot \sin {\rm{x}} + {\rm{b}} \cdot \cos {\rm{x}}}}{{c \cdot \sin {\rm{x}} + {\rm{d}} \cdot \cos {\rm{x}} + {\rm{e}}}}$	$t = \tan \frac{x}{2};\left( {\cos \frac{{\rm{x}}}{2} \ne 0} \right)$
Hàm $f(x) = \frac{1}{{\sqrt {(x + a)(x + b)} }}$	Với : x + a > 0 và x + b > 0 Đặt $:t = \sqrt {x + a} + \sqrt {x + b} $ Với x + a < 0 và x + b < 0 Đặt $t = \sqrt {x - a} + \sqrt { - x - b} $

2. Nguyên hàm từng phần

Nếu u(x), v(x) là hai hàm số có đạo hàm liên tục trên K :

$\int u (x) \cdot {v^\prime }(x)dx = u(x) \cdot v(x) - \int v (x) \cdot {u^\prime }(x)dx$

Hay $\int u dv = uv - \int v du\left( {} \right.$ với $du = {u^\prime }(x)dx,dv = {v^\prime }(x)dx$ )

Phương pháp chung

- Bước 1: Ta biến đổi tích phân ban đầu về dạng :

$$I = \int f (x)dx = \int {{f_1}} (x) \cdot {f_2}(x)dx$$

Bước 2: Đặt : $\left\{ {\begin{array}{*{20}{l}}{u = {f_1}(x)}\\{dv = {f_2}(x)}\end{array} \to \left\{ {\begin{array}{*{20}{l}}{du = f_1^1(x)dx}\\{v = \int {{f_2}} (x)dx}\end{array}} \right.} \right.$

Bước 3: Khi đó: $\quad \int u .dv = u.v - \int v \cdot du$

Dạng I. $I = \int P (x)\left\{ {\begin{array}{*{20}{l}}{\sin x}\\{\cos x}\\{{e^x}}\end{array}} \right\} \cdot dx$

Đặt \[\left\{ {\begin{array}{*{20}{l}}{u = P(x)}\\{dv = \left\{ {\begin{array}{*{20}{l}}{\sin x}\\{\cos x}\\{{e^x}}\end{array}} \right\}dx}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{u^\prime }du = {P^\prime }(x)dx}\\{v = \left\{ {\begin{array}{*{20}{l}}{ - \cos x}\\{\sin x}\\{{e^x}}\end{array}} \right\}}\\{}\end{array}} \right.} \right.\]

Vậy \[{\rm{ }}I = P(x)\left\{ {\begin{array}{*{20}{l}}{ - \cos x}\\{\sin x}\\{{e^x}}\end{array}} \right\} - \smallint \left\{ {\begin{array}{*{20}{l}}{ - \cos x}\\{\sin x}\\{{e^x}}\end{array}} \right\}{P^\prime }(x)dx\]

Dạng II$:I = \int P (x) \cdot \ln xdx$

Đặt${\rm{ }}\left\{ {\begin{array}{*{20}{l}}{u = l n x}\\{dv = P(x)dx}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{du = \frac{1}{x}dx}\\{v = \int P (x)dx = Q(x)}\end{array}{\rm{ }}} \right.} \right.$

Vậy${\rm{ }}I = \ln x \cdot Q(x) = \int Q (x) \cdot \frac{1}{x}dx$

Dạng III : $I = \int {{e^x}} \left\{ {\begin{array}{*{20}{l}}{\sin x}\\{\cos x}\end{array}} \right\}dx$

Đặt$\left\{ {\begin{array}{*{20}{l}}{u = {e^x}}\\{dv = \{ \begin{array}{*{20}{l}}{ s i n x}\\{ c o s x}\end{array}\} \cdot dx}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{du = {e^x}dx}\\{v = \left\{ {\begin{array}{*{20}{c}}{ - \cos x}\\{\sin x}\end{array}} \right\}}\end{array}} \right.} \right.$

Vậy $I = {e^x}\left\{ {\begin{array}{*{20}{l}}{ - \cos x}\\{\sin x}\end{array}} \right\} - \smallint \left\{ {\begin{array}{*{20}{l}}{ - \cos x}\\{\sin x}\end{array}} \right\}{e^x}dx$.

Bằng phương pháp tương tự tính được $\smallint \left\{ {\begin{array}{*{20}{l}}{ - \cos x}\\{\sin x}\end{array}} \right\}{e^x}dx$ sau đó thay vào I ra kết quả.

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10

Tài liệu có 67 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm

Tài Liệu Xem Nhiều

pdf Các công thức mặt nón, mặt cầu, mặt trụ
2 35.8 K 82
pdf Góc giữa cạnh bên và mặt đáy
3 35 K 70
pdf Phương pháp ghép trục trong bài toán hàm hợp
48 24.5 K 321
pdf 50 Bài tập Nguyên hàm (có đáp án)- Toán 12
22 23.8 K 346
pdf Vị trí tương đối của đường thẳng và mặt phẳng
9 21.3 K 27

1. \(\int 0 dx = C\quad \)	16. \(\int {{{(ax + b)}^\alpha }} {\rm{dx}} = \frac{1}{a}\frac{{{{(ax + b)}^{\alpha + 1}}}}{{\alpha + 1}} + c,\alpha \ne - 1\)
2. \(\int d x = x + C\)	17. \(\int {\frac{1}{{{{(ax + b)}^2}}}} dx = - \frac{1}{a} \cdot \frac{1}{{ax + b}} + C\)
3. \(\int {{x^\alpha }} dx = \frac{1}{{\alpha + 1}}{x^{\alpha + 1}} + C(\alpha \ne - 1)\)	18. \(\int {\frac{{dx}}{{ax + b}}} = \frac{1}{a}\ln \|ax + b\| + C\)
4. \(\int {\frac{1}{{{x^2}}}} dx = - \frac{1}{x} + C\)	19. \(\int {{e^{ax + b}}} dx = \frac{1}{a}{e^{ax + b}} + C\) 20. \(\int {{a^{k + h}}} dx = \frac{1}{k}\frac{{{a^{k + \delta }}}}{{\ln a}} + C\)
5. \(\int {\frac{1}{x}} dx = \ln \|x\| + C\)	21. \(\int {\cos } (ax + b)dx = \frac{1}{a}\sin (ax + b) + C\)
6. \(\int {{e^x}} dx = {e^x} + C\)	22. \(\int {\sin } (ax + b)dx = - \frac{1}{a}\cos (ax + b) + C\)
7. \(\int {{a^x}} dx = \frac{{{a^x}}}{{\ln a}} + C\)	23. \(\int {\tan } (ax + b)dx = - \frac{1}{a}\ln \|\cos (ax + b)\| + C\)
8. \(\int {\cos } xdx = \sin x + C\)	24. \(\int {\cot } (ax + b)dx = \frac{1}{a}\ln \|\sin (ax + b)\| + C\)
9. \(\int {\sin } xdx = - \cos x + C\)	25. \(\int {\frac{1}{{{{\cos }^2}(ax + b)}}} dx = \frac{1}{a}\tan (ax + b) + C\)
10. \(\int {\tan } x \cdot dx = - \ln \|\cos x\| + C\)	26. \(\int {\frac{1}{{{{\sin }^2}(ax + b)}}} dx = - \frac{1}{a}\cot (ax + b) + C\)
11. \(\int {\cot } xdx = \ln \|\sin x\| + C\)	27. \(\int {\left( {1 + {{\tan }^2}(ax + b)} \right)} dx = \frac{1}{a}\tan (ax + b) + C\)
12. \(\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C\)	28. \(\int {\left( {1 + {{\cot }^2}(ax + b)} \right)} dx = - \frac{1}{a}\cot (ax + b) + C\)
13. \(\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\)
14. \(\int {\left( {1 + {{\tan }^2}x} \right)} dx = \tan x + C\)
15. \(\int {\left( {1 + {{\cot }^2}x} \right)} dx = - \cot x + C\)

\(\int {\frac{{dx}}{{{a^2} + {x^2}}}} = \frac{1}{a}\arctan \frac{x}{a} + C\)	\(\int {\arcsin } \frac{x}{a}dx = x\arcsin \frac{x}{a} + \sqrt {{a^2} - {x^2}} + C\)
\(\int {\frac{{dx}}{{{a^2} - {x^2}}}} = \frac{1}{{2a}}\ln \left\| {\frac{{a + x}}{{a - x}}} \right\| + C\)	\(\int {\arccos } \frac{x}{a}dx = x\arccos \frac{x}{a} - \sqrt {{a^2} - {x^2}} + C\)
\(\int {\frac{{dx}}{{\sqrt {{x^2} + {a^2}} }}} = \ln \left( {x + \sqrt {{x^2} + {a^2}} } \right) + C\)	\(\int {\arctan } \frac{x}{a}dx = x\arctan \frac{x}{a} - \frac{a}{2}\ln \left( {{a^2} + {x^2}} \right) + C\)
\(\int {\frac{{dx}}{{\sqrt {{a^2} - {x^2}} }}} = \arcsin \frac{x}{{\|a\|}} + C\)	\(\int {{\mathop{\rm arccot}\nolimits} } \frac{x}{a}dx = x{\mathop{\rm arccot}\nolimits} \frac{x}{a} + \frac{a}{2}\ln \left( {{a^2} + {x^2}} \right) + C\)
\(\int {\frac{{dx}}{{x\sqrt {{x^2} - {a^2}} }}} = \frac{1}{a}\arccos \left\| {\frac{x}{a}} \right\| + C\)	\(\int {\frac{{dx}}{{\sin (ax + b)}}} = \frac{1}{a}\ln \left\| {\tan \frac{{ax + b}}{2}} \right\| + C\)
\(\int {\frac{{dx}}{{x\sqrt {{x^2} + {a^2}} }}} = - \frac{1}{a}\ln \left\| {\frac{{a + \sqrt {{x^2} + {a^2}} }}{x}} \right\| + C\)	\(\int {\frac{{dx}}{{\sin (ax + b)}}} = \frac{1}{a}\ln \left\| {\tan \frac{{ax + b}}{2}} \right\| + C\)
\(\int {\ln } (ax + b)dx = \left( {x + \frac{b}{a}} \right)\ln (ax + b) - x + c\)	\(\int {{e^{ax}}} \cos bxdx = \frac{{{e^{ax}}(a\cos bx + b\sin bx)}}{{{a^2} + {b^2}}}\)
\(\int {\sqrt {{a^2} - {x^2}} } dx = \frac{{x\sqrt {{a^2} - {x^2}} }}{2} + \frac{{{a^2}}}{2}\arcsin \frac{x}{a} + C\)	\(\int {\sin } bxdx = \frac{{{e^{ax}}(a\sin bx - b\cos bx)}}{{{a^2} + {b^2}}} + C\)

Dấu hiệu	Cách chọn
\(\sqrt {{a^2} - {x^2}} \)	Đặt \(x = \|a\|\sin t;\) với \(t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \cdot \) hoặc \(x = \|a\|\cos t;\) với \(t \in [0;\pi ].\)
\(\sqrt {{x^2} - {a^2}} \)	Đặt \(x = \frac{{\|{\rm{a}}\|}}{{\sin t}} \cdot ;\) với \(t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\backslash \{ 0\} \) hoặc \(x = \frac{{\|a\|}}{{\cos t}}\) với\(t \in [0;\pi ]\backslash \left\{ {\frac{\pi }{2}} \right\}.\)
\(\sqrt {{a^2} + {x^2}} \)	Đặt \(x = a\tan t;\) với \(t \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right).\) hoặc x = \|a\|cott với \(t \in [0;\pi ].\)
\(\sqrt {\frac{{a + x}}{{a - x}}} .\) hoặc \(\sqrt {\frac{{a - x}}{{a + x}}} .\)	Đặt \(x = a\cos 2t\)
\(\sqrt {(x - a)(b - x)} \)	Đặt \(x = a + (b - a){\sin ^2}t\)
\(\frac{1}{{{a^2} + {x^2}}}\)	Đặt \(x = a\tan t;\) với \(t \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right).\)

Dấu hiệu	Cách chọn
Hàm số mẫu số có	t là mẫu số
Hàm \(f(x;\sqrt {\varphi (x)} )\)	\(t = \sqrt {\varphi (x)} \)
Hàm \(f(x) = \frac{{a \cdot \sin {\rm{x}} + {\rm{b}} \cdot \cos {\rm{x}}}}{{c \cdot \sin {\rm{x}} + {\rm{d}} \cdot \cos {\rm{x}} + {\rm{e}}}}\)	\(t = \tan \frac{x}{2};\left( {\cos \frac{{\rm{x}}}{2} \ne 0} \right)\)
Hàm \(f(x) = \frac{1}{{\sqrt {(x + a)(x + b)} }}\)	Với : x + a > 0 và x + b > 0 Đặt \(:t = \sqrt {x + a} + \sqrt {x + b} \) Với x + a < 0 và x + b < 0 Đặt \(t = \sqrt {x - a} + \sqrt { - x - b} \)